M8 Bruchgleichungen: Unterschied zwischen den Versionen

Version vom 1. Mai 2020, 11:17 Uhr

  Aufgabe 1

Bevor du Bruchgleichungen kennenlernst, wiederhole das Lösen von Gleichungen mit Äquivalenzumformungen aus der 7. Klasse.
Bearbeite dazu in Mathegym den Arbeitsauftrag Wiederholung 7. Klasse: Lösen von Gleichungen

Zu Beginn der Bruchterme haben wir gebrochen-rationale Funktionen betrachtet. Im folgenden Bild sind die zwei Graphen der Funktionen 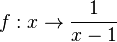und 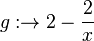gezeichnet.

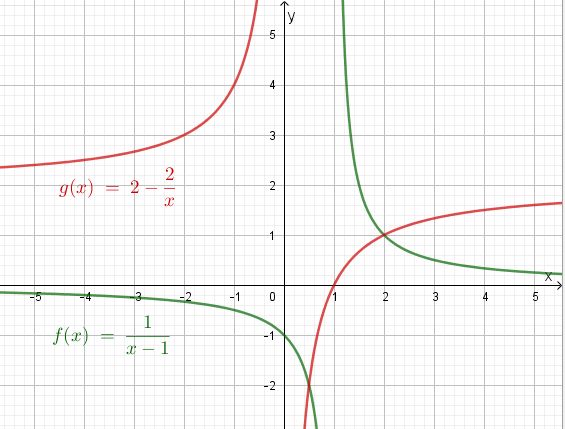
Die zwei Graphen schneidet sich in zwei Punkten. Die Koordinaten des rechten Schnittpunkts S kann man ablesen. Es ist S(2;1). Die Koordinaten des zweiten Schnittpunkte T kann man nicht so leicht ablesen. Es könnte T(0,5;-2) sein. Aber ist man sich sicher?

Bei der Behandlung linearer Funktionen hatten wir auch schon den Schnittpunkt zweier Geraden. Wir haben die Geraden gezeichnet und aus dem Diagramm den Schnittpunkt abgelesen. Wir haben aber auch den Schnittpunkt berechnet, indem wir die zwei Geradengleichungen gleichgesetzt haben. Dieses Rechenverfahren wollen wir nun hier bei unseren zwei Hyperbeln auch anwenden. Im Schnittpunkt haben beide Funktionsgraphen den gleichen x- und den gleichen y-Wert. Wir setzen die beiden Funktionsterme (gleiche y-Werte) gleich 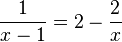. Nun muss man diese Gleichung lösen und erhält die x-Koordinate des Schnittpunktes.

Merke: Eine Bruchgleichung ist eine Gleichung mit mindestens einem Bruch, der die Unbekannte im Nenner enthält.

Wie löst man nun eine Bruchgleichung?