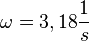Die Tacoma-Narrows-Brücke: Unterschied zwischen den Versionen
(→Gewollte Resonanz) |
(→Gewollte Resonanz) |
||
| (7 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
{{Aufgaben-blau|1|2=Schaue dir dieses Video an:<br> | {{Aufgaben-blau|1|2=Schaue dir dieses Video an:<br> | ||
Anregung und Resonanz beim Federpendel: {{#ev:youtube |FvtwYwTRJq0|350}}<br> | Anregung und Resonanz beim Federpendel: {{#ev:youtube |FvtwYwTRJq0|350}}<br> | ||
| − | Beschreibe und erkläre den Versuch. | + | a) Beschreibe und erkläre den Versuch. |
| − | {{Lösung versteckt|Ein Federpendel wird durch einen Exzenter zu Schwingungen angeregt. Der Exzenter dreht sich mit der Winkelgeschwindigkeit <math>\omega</math>, welche variiert werden kann, und hat die Erregerfrequenz <math>f</math>. Ist <math>\omega</math> klein, so schwingt das Federpendel mit der Erregerfrequenz <math>f (\omega = 2\pi f)</math>, seine Amplitude ist klein. Exzenter und Federpendel sind synchron. <br> | + | b) Was versteht man unter Eigenfrequenz, was unter Erregerfrequenz? |
| + | }} | ||
| + | |||
| + | {{Lösung versteckt|a) Ein Federpendel wird durch einen Exzenter zu Schwingungen angeregt. Der Exzenter dreht sich mit der Winkelgeschwindigkeit <math>\omega</math>, welche variiert werden kann, und hat die Erregerfrequenz <math>f</math>. Ist <math>\omega</math> klein, so schwingt das Federpendel mit der Erregerfrequenz <math>f (\omega = 2\pi f)</math>, seine Amplitude ist klein. Exzenter und Federpendel sind synchron. <br> | ||
Wird <math>\omega</math> des Exzenters gesteigert, dann nimmt die Ampltude des Federpendels zu. Stimmt die Erregerfrequenz <math>f</math> mit der Eigenfrequenz <math> f_0</math> des Federpendels überein, dann hat das Federpendel eine gewaltige Amplitude und die Schwingung erfolgt um <math>\frac{\pi}{2}</math> phasenverschoben. <br> | Wird <math>\omega</math> des Exzenters gesteigert, dann nimmt die Ampltude des Federpendels zu. Stimmt die Erregerfrequenz <math>f</math> mit der Eigenfrequenz <math> f_0</math> des Federpendels überein, dann hat das Federpendel eine gewaltige Amplitude und die Schwingung erfolgt um <math>\frac{\pi}{2}</math> phasenverschoben. <br> | ||
Steigert man die Erregerfrequenz weiter dann nimmt die Amplitude ab und die Erregerschwingung und Federschwingung sind gegenphasig (Phasenverschiebung <math>\pi</math>. | Steigert man die Erregerfrequenz weiter dann nimmt die Amplitude ab und die Erregerschwingung und Federschwingung sind gegenphasig (Phasenverschiebung <math>\pi</math>. | ||
| + | |||
| + | b) Die Eigenfrequenz ist die Frequenz mit der ein schwingungsfähiges System nach Anregung schwingt. <br> | ||
| + | Die Erregerfrequenz ist die Frequenz mit der der Erreger seine periodische Bewegung macht. | ||
}} | }} | ||
| Zeile 13: | Zeile 19: | ||
Resonanz kann man beim [https://www.leifiphysik.de/mechanik/kopplung-von-schwingungen/versuche/resonanz-am-federpendel Federpendel] gut beobachten. Eine schöne [https://www.leifiphysik.de/mechanik/kopplung-von-schwingungen/versuche/erzwungene-schwingung-eines-federpendels-simulation Simulation zur Erregung eines Federpendels]. | Resonanz kann man beim [https://www.leifiphysik.de/mechanik/kopplung-von-schwingungen/versuche/resonanz-am-federpendel Federpendel] gut beobachten. Eine schöne [https://www.leifiphysik.de/mechanik/kopplung-von-schwingungen/versuche/erzwungene-schwingung-eines-federpendels-simulation Simulation zur Erregung eines Federpendels]. | ||
| − | {{Versuch|1=Beschreibe die Simulation und erkläre, was im Graph dargestellt wird. | + | {{Versuch|1=Beschreibe die [https://www.leifiphysik.de/mechanik/kopplung-von-schwingungen/versuche/erzwungene-schwingung-eines-federpendels-simulation Simulation] und erkläre, was im Graph dargestellt wird. |
| + | |||
| + | Was bewirkt eine Veränderung der Federhärte D, der Masse m? | ||
Bestimme die Kreisfreqnenz <math>\omega</math> der Erregerschwingung, bei der die Amplitude der Schwingung des Federpendels am größten wird.}} | Bestimme die Kreisfreqnenz <math>\omega</math> der Erregerschwingung, bei der die Amplitude der Schwingung des Federpendels am größten wird.}} | ||
| Zeile 22: | Zeile 30: | ||
Die lila Pfeile neben dem Pendel geben die Amplitude der Schwingung des Federpendels an.<br> | Die lila Pfeile neben dem Pendel geben die Amplitude der Schwingung des Federpendels an.<br> | ||
Im Diagramm wird über der Kreisfrequenz <math>\omega</math> die Amplitude der Schwingung des Federpendels aufgetragen. | Im Diagramm wird über der Kreisfrequenz <math>\omega</math> die Amplitude der Schwingung des Federpendels aufgetragen. | ||
| + | |||
| + | Über <math>\omega_0 = \sqrt{\frac{D}{m}}</math> bestimmen D und m die Eigenfrequenz des Federpendels. Ändert man den Wert von D oder m, dann ergibt sich eine andere Eigenfrequenz der Federpendelschwingung. | ||
<math>\omega = 3,18 \frac{1}{s}</math>}} | <math>\omega = 3,18 \frac{1}{s}</math>}} | ||
| Zeile 32: | Zeile 42: | ||
Zusammenfassung Resonanz und Resonanzkatastrophe: {{#ev:youtube |xcjv_vQJO7U|350}} oder {{#ev:youtube |0Gzi-5CRJ3A|350}} | Zusammenfassung Resonanz und Resonanzkatastrophe: {{#ev:youtube |xcjv_vQJO7U|350}} oder {{#ev:youtube |0Gzi-5CRJ3A|350}} | ||
| − | {{Aufgaben-blau||2=Erkläre den Begriff Resonanz.}} | + | {{Aufgaben-blau|2|2=Erkläre den Begriff Resonanz.}} |
{{Lösung versteckt|Ein schwingungsfähiges System (z.B. ein Federpendel) mit der Eigenschwingungsfrequenz f<sub>0</sub> wird durch eine Erregerschwingung zu Schwingungen angeregt. Ist die Erregerfrequenz f << f<sub>0</sub> so schwingt das System mit der Erregerfrequenz f. Stimmt die Erregerfrequenz f mit der Eigenschwingungsfrequenz f<sub>0</sub> überein so nimmt die Amplitude der Schingung gewaltig zu. Dies kann auch zur Zerstörung des Systems führen. Dies ist der Resonanzfall. Nimmt f weiter zu, dann nimmt die Amplitude ab und geht gegen 0.}} | {{Lösung versteckt|Ein schwingungsfähiges System (z.B. ein Federpendel) mit der Eigenschwingungsfrequenz f<sub>0</sub> wird durch eine Erregerschwingung zu Schwingungen angeregt. Ist die Erregerfrequenz f << f<sub>0</sub> so schwingt das System mit der Erregerfrequenz f. Stimmt die Erregerfrequenz f mit der Eigenschwingungsfrequenz f<sub>0</sub> überein so nimmt die Amplitude der Schingung gewaltig zu. Dies kann auch zur Zerstörung des Systems führen. Dies ist der Resonanzfall. Nimmt f weiter zu, dann nimmt die Amplitude ab und geht gegen 0.}} | ||
| Zeile 50: | Zeile 60: | ||
Im [https://www.youtube.com/watch?v=xcjv_vQJO7U Video von SimplePhysics] wird der Einsturz erklärt. | Im [https://www.youtube.com/watch?v=xcjv_vQJO7U Video von SimplePhysics] wird der Einsturz erklärt. | ||
| − | Der Einsturz der Brücke ist auf dieser [ | + | Der Einsturz der Brücke ist auf dieser [https://www.leifiphysik.de/mechanik/kopplung-von-schwingungen/ausblick/resonanzbruecke Seite] kurz und gut erklärt. |
=Gewollte Resonanz= | =Gewollte Resonanz= | ||
| Zeile 59: | Zeile 69: | ||
{{Lösung versteckt|1=Gitarre, Geige, Klavier, Schlagzeug, Schlaginstrumente, Orgel, Blasinstrumente, ... }} | {{Lösung versteckt|1=Gitarre, Geige, Klavier, Schlagzeug, Schlaginstrumente, Orgel, Blasinstrumente, ... }} | ||
| + | |||
| + | {{Aufgaben-blau|3|Bei manchen Schwingungen will man keine Dämpfung, bei anderen Schwingungen braucht man eine große Dämpfung. Überlege dir Fälle wo man schwache Dämpfung bzw. eine starke Dämpfung haben will.}} | ||
| + | |||
| + | {{Lösung versteckt|Bei Musikinstrumenten will man sicher nur eine schwache Dämpfung, damit ein voller Ton erzeugt wird. <br> | ||
| + | Bei der Feder eines Stoßdämpfers beim Auto will man eine große Dämpfung, damit das Auto nicht lange nachschwingt, sondern nur ausgelenkt wird und gleich wieder in die Nulllage zurückkehrt (aperiodischer Grenzfall).}} | ||
| + | |||
| + | <center> | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | {{#ev:youtube |g765bRh51wo|250}} || {{#ev:youtube |lFWXjzhH8a0|250}} || {{#ev:youtube |E_ZBELcyb3g|250}} | ||
| + | |- | ||
| + | | {{#ev:youtube |e13zPsgkytw|250}} || {{#ev:youtube |XKRj-T4l-e8|250}} || | ||
| + | </center> | ||
Aktuelle Version vom 6. Mai 2020, 07:24 Uhr
Inhaltsverzeichnis[Verbergen] |
Was ist Resonanz
Resonanz kann man beim Federpendel gut beobachten. Eine schöne Simulation zur Erregung eines Federpendels.
|
Beschreibe die Simulation und erkläre, was im Graph dargestellt wird. Was bewirkt eine Veränderung der Federhärte D, der Masse m? Bestimme die Kreisfreqnenz |
Auf dieser Seite ist erklärt, was man unter Resonanz versteht.
Bearbeite dieses Arbeitsblatt mit dem Applet.
Die Tacoma-Narrows-Brücke
Die erste Tacoma-Narrows-Brücke wurde durch eine Resonanzerscheinung berühmt, durch die sie dann leider auch zerstört wurde. Eine ausführliche Information zur Brücke findet man bei Wikipedia.
Die Brücke war mit einer Mittelspannweite von 853 Metern zum Zeitpunkt ihrer Fertigstellung die drittgrößte Hängebrücke der Welt. Sie wurde am 1. Juli 1940 eröffnet.
Bei Brücken dieser Art war bekannt, dass sich entlang der Brücke Transversalwellen ausbilden können. Schon durch leichten Wind wurde die Brücke zu Eigenschwingungen angeregt und geriet in Resonanz. Daher auch der Beiname "Galloping Gertie".
Würde man mit dem Auto über diese Brücke fahren wollen?
Diese angeregte Querschwingung trug aber nicht zur Zerstörung der Brücke bei, sondern die Brücke stürzte am 7. November 1940 durch eine unerwartet aufgetretene Torsionsschwingung ein.
Zerstörerisch wirkte allerdings die Torsionsschwingung
Erklärung
Im Video von SimplePhysics wird der Einsturz erklärt.
Der Einsturz der Brücke ist auf dieser Seite kurz und gut erklärt.
Gewollte Resonanz
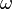 , welche variiert werden kann, und hat die Erregerfrequenz
, welche variiert werden kann, und hat die Erregerfrequenz  . Ist
. Ist  , seine Amplitude ist klein. Exzenter und Federpendel sind synchron.
, seine Amplitude ist klein. Exzenter und Federpendel sind synchron.  des Federpendels überein, dann hat das Federpendel eine gewaltige Amplitude und die Schwingung erfolgt um
des Federpendels überein, dann hat das Federpendel eine gewaltige Amplitude und die Schwingung erfolgt um 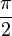 phasenverschoben.
phasenverschoben.  .
.
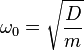 bestimmen D und m die Eigenfrequenz des Federpendels. Ändert man den Wert von D oder m, dann ergibt sich eine andere Eigenfrequenz der Federpendelschwingung.
bestimmen D und m die Eigenfrequenz des Federpendels. Ändert man den Wert von D oder m, dann ergibt sich eine andere Eigenfrequenz der Federpendelschwingung.