M11 Rechnen mit Vektoren: Unterschied zwischen den Versionen
| (17 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 10: | Zeile 10: | ||
Rechnerisch heißt das, dass man die Koordinaten der Vektoren addiert, man spricht von koordinatenweiser Addition. <br> | Rechnerisch heißt das, dass man die Koordinaten der Vektoren addiert, man spricht von koordinatenweiser Addition. <br> | ||
| − | Für die Vektoren <math>\vec u = \left ( \begin{array}{c} u_1 \\\ u_2 \\\ u_3 \end{array}\right) </math> und <math>\vec v = \left ( \begin{array}{c} v_1 \\\ v_2 \\\ v_3 \end{array}\right) </math> gilt dann für den Summenvektor <math>\vec w = \vec u + \vec v = \left ( \begin{array}{c} u_1 \\\ u_2 \\\ u_3 \end{array}\right) + \left ( \begin{array}{c} v_1 \\\ v_2 \\\ v_3 \end{array}\right)= \left ( \begin{array}{c} u_1+v_1 \\\ u_2+v_2 \\\ u_3+v_3 \end{array}\right) </math> | + | Für die Vektoren <math>\vec u = \left ( \begin{array}{c} u_1 \\\ u_2 \\\ u_3 \end{array}\right) </math> und <math>\vec v = \left ( \begin{array}{c} v_1 \\\ v_2 \\\ v_3 \end{array}\right) </math> gilt dann für den Summenvektor <math>\vec w = \vec u + \vec v = \left ( \begin{array}{c} u_1 \\\ u_2 \\\ u_3 \end{array}\right) + \left ( \begin{array}{c} v_1 \\\ v_2 \\\ v_3 \end{array}\right)= \left ( \begin{array}{c} u_1+v_1 \\\ u_2+v_2 \\\ u_3+v_3 \end{array}\right) </math> .<br> |
Die Koordinaten des Summenvektors sind die Summen der Koordinaten der Summanden. | Die Koordinaten des Summenvektors sind die Summen der Koordinaten der Summanden. | ||
| + | |||
| + | Beispiele: <math>\left ( \begin{array}{c} 1 \\\ 2 \\\ 3 \end{array}\right) + \left ( \begin{array}{c} 3 \\\ 2 \\\ 1 \end{array}\right)= \left ( \begin{array}{c} 1+3 \\\ 2+2 \\\ 3+1 \end{array}\right)= \left ( \begin{array}{c} 4 \\\ 4 \\\ 4 \end{array}\right)</math> <br> | ||
| + | <math>\left ( \begin{array}{c} -1 \\\ 0 \\\ 2 \end{array}\right) + \left ( \begin{array}{c} 3 \\\ -2 \\\ 1 \end{array}\right)= \left ( \begin{array}{c} -1+3 \\\ 0-2 \\\ 2+1 \end{array}\right)= \left ( \begin{array}{c} 2 \\\ -2 \\\ 3 \end{array}\right)</math> | ||
| + | |||
Für die Vektoraddition gelten auch Rechengesetze. Aus der Algebra kennt man für das Rechnen mit Buchstaben das Kommutativgesetz und das Assoziativgesetz. Diese Gesetze gelten auch für Vektoren. Das Kommutativgesetz sieht man sehr einfach bei der Konstruktion des Summenvektors: [[Datei:Wektory_sumr.svg]]<br> | Für die Vektoraddition gelten auch Rechengesetze. Aus der Algebra kennt man für das Rechnen mit Buchstaben das Kommutativgesetz und das Assoziativgesetz. Diese Gesetze gelten auch für Vektoren. Das Kommutativgesetz sieht man sehr einfach bei der Konstruktion des Summenvektors: [[Datei:Wektory_sumr.svg]]<br> | ||
| Zeile 19: | Zeile 23: | ||
<ggb_applet height="500" width="700" | <ggb_applet height="500" width="700" | ||
filename="Vektoren3.ggb" /> | filename="Vektoren3.ggb" /> | ||
| − | Verändert man die Vektoren <math>\vec u , \vec v</math> oder <math>\vec w</math> so ergibt sich stets der gleiche schwarze Pfeil als <math>(\vec u + \vec ) + \vec w</math> oder <math>\vec u + (\vec v + \vec w )</math>. | + | Verändert man die Vektoren <math>\vec u , \vec v</math> oder <math>\vec w</math> so ergibt sich stets der gleiche schwarze Pfeil als <math>(\vec u + \vec v ) + \vec w</math> oder <math>\vec u + (\vec v + \vec w )</math>. |
| + | |||
| + | |||
| + | Vektoren eignen sich prina für Wege von A nach B. Macht man einen Umweg über C, dann gehe entlang der Vektoren <math>\vec {AC}</math> und <math>\vec {CB}</math>, also gehe mit dem Summenvektor <math>\vec {AC} + \vec {CB}</math>. <br> | ||
| + | <center>[[Datei:Vektoren.jpg]]</center><br> | ||
| + | Um von A über C nach B zu kommen kann man aber auch statt <math>\vec {AC} + \vec {CB}</math> eine Abkürzung nehmen, nämlich <math>\vec {AB}</math>. | ||
| + | |||
| + | {{Aufgaben-blau|1|2=1. Wie ist der Weg von B nach A<br> | ||
| + | a) direkt?<br> | ||
| + | b) über C?<br> | ||
| + | 2. Wie ist der Weg von C nach B<br> | ||
| + | a) direkt?<br> | ||
| + | b) über A? }} | ||
| + | |||
| + | {{Lösung versteckt|1=1a) <math>\vec {BA} = -\vec {AB}</math><br> | ||
| + | b) <math>\vec {BC} + \vec {CA}</math><br> | ||
| + | 2a) <math>\vec {CB}</math><br> | ||
| + | b) <math>\vec {CA} + \vec {CB}</math> | ||
| + | }} | ||
| + | |||
| + | |||
| + | {{Merke|1='''S-Multiplikation'''<br> | ||
| + | Vektoren können mit reellen Zahlen (Skalare genannt) multipliziert werden. Die Länge des resultierenden Vektors u ist daher c*u. Man denke an eine zentrische Streckung. Wenn der Skalar c positiv ist, zeigt der resultierende Vektor in dieselbe Richtung, ist c negativ, in die Gegenrichtung. | ||
| + | <ggb_applet height="500" width="700" | ||
| + | filename="Vektoren4.ggb" /><br> | ||
| + | Durch Ziehen am Schieberegler verändert man den Wert von c. Der rote Vektor <math>\vec v</math> ist der Vektor, der sich durch die Multiplikation des Vektors <math>\vec u</math> mit der reellen Zahl c ergibt. <math> \vec v = c\cdot \vec u</math>. <br> | ||
| + | |||
| + | Jede Koordinate des Vektors <math>\vec u</math> wird mit c multipliziert. Man spricht von koordinatenweiser Multiplikation. <br> | ||
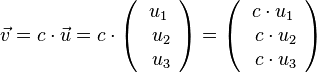
| + | <math>\vec v = c \cdot \vec u = c \cdot \left ( \begin{array}{c} u_1 \\\ u_2 \\\ u_3 \end{array}\right) = \left ( \begin{array}{c} c \cdot u_1 \\\ c \cdot u_2 \\\ c \cdot u_3 \end{array}\right)</math> | ||
| + | }} | ||
| + | |||
| + | Beispiele: <math>3\cdot \left ( \begin{array}{c} 1 \\\ 2 \\\ 3 \end{array}\right) = \left ( \begin{array}{c} 3 \\\ 6 \\\ 9 \end{array}\right)</math><br> | ||
| + | <math>-1\cdot \left ( \begin{array}{c} 1 \\\ 2 \\\ 3 \end{array}\right) = \left ( \begin{array}{c} -1 \\\ -2 \\\ -3 \end{array}\right)</math> Beachte: <math> \vec v</math> ist der Gegenvektor zu <math>\vec u </math>.<br> | ||
| + | <math>5\cdot \left ( \begin{array}{c} 3 \\\ 0 \\\ -2 \end{array}\right) = \left ( \begin{array}{c} 15 \\\ 0 \\\ -10 \end{array}\right)</math><br> | ||
| + | |||
| + | |||
| + | {{Merke|1=Man sieht, dass das Rechnen mit Vektoren genauso geht wie das Rechnen in der Algebra mit Buchstaben und Zahlen, nur dass nun über den Buchstaben noch ein Vektorpfeil istl. Es gibt die Vektoraddition mit der man Vektoren addieren kann und die S-Multiplikation, bei der Vektoren mit reellen Zahlen multipliziert werden. Das geht genauso wie man es bisher beim Rechnen mit Zahlen und Buchstaben kennengelernt hat. <br> | ||
| + | Eines aber darf man nicht. Man darf nicht durch Vektoren dividieren.<br> | ||
| + | Dazu bräuchte man eine Multiplikation zwischen Vektoren, welche bisher (noch) nicht vorkommt. }} | ||
| + | |||
| + | |||
| + | {{Aufgaben-blau|2|2=Buch S. 97 / 1 | ||
| + | |||
| + | {{Lösung versteckt|1=Die Vektoren sind <math>\vec a = \left ( \begin{array}{c} 1 \\\ 3 \end{array}\right), \vec b = \left ( \begin{array}{c} 2 \\\ 2 \end{array}\right), \vec c = \left ( \begin{array}{c} 3 \\\ 0 \end{array}\right), \vec d = \left ( \begin{array}{c} 0 \\\ -3 \end{array}\right), \vec e = \left ( \begin{array}{c} -3 \\\ -2 \end{array}\right)</math><br> | ||
| + | a) <math>\vec a - \vec b = \left ( \begin{array}{c} 1 \\\ 3 \end{array}\right) - \left ( \begin{array}{c} 2 \\\ 2 \end{array}\right)= \left ( \begin{array}{c} -1 \\\ 1 \end{array}\right)</math><br> | ||
| + | b) <math>\vec c - \vec d = \left ( \begin{array}{c} 3 \\\ 0 \end{array}\right) + \left ( \begin{array}{c} 0 \\\ -3 \end{array}\right)= \left ( \begin{array}{c} 3 \\\ -3 \end{array}\right)</math><br> | ||
| + | c) <math>2\vec a + \vec e = 2\left ( \begin{array}{c} 1 \\\ 3 \end{array}\right) + \left ( \begin{array}{c} -3 \\\ -2 \end{array}\right)= \left ( \begin{array}{c} -1 \\\ 4 \end{array}\right)</math><br> | ||
| + | d) <math>-\vec a - \vec b +\vec c -\vec e= -\left ( \begin{array}{c} 1 \\\ 3 \end{array}\right) - \left ( \begin{array}{c} 2 \\\ 2 \end{array}\right) + \left ( \begin{array}{c} 3 \\\ 0 \end{array}\right) - \left ( \begin{array}{c} -3 \\\ -2 \end{array}\right)= | ||
| + | = \left ( \begin{array}{c} 3 \\\ -3 \end{array}\right)</math><br> | ||
| + | e) <math>2\vec c + \vec d - \vec a = 2\left ( \begin{array}{c} 3 \\\ 0 \end{array}\right) + \left ( \begin{array}{c} 0 \\\ -3 \end{array}\right) - \left ( \begin{array}{c} 1 \\\ 3 \end{array}\right) = \left ( \begin{array}{c} 5 \\\ -6 \end{array}\right)</math> | ||
| + | |||
| + | Man kann die Vektoren der Aufgaben a) - e) in der Zeichenebene auch gut zeichnen und die Ergebnisse verifizieren. }} | ||
| + | |||
| + | |||
| + | Buch S. 97 / 2 | ||
| + | |||
| + | {{Lösung versteckt|1= a) wahr, b) wahr, c) falsch, d) wahr, e) wahr, f) wahr }} }} | ||
| + | |||
| + | {{Aufgaben-blau|3|2=Buch S. 97 / 4 | ||
| + | |||
| + | {{Lösung versteckt|1)a) <math>2A(\vec a + \vec b ) + \vec a = 3 \vec a + 2 \vec b</math><br> | ||
| + | b) <math>5(\vec a + \vec b ) + 3(\vec a - \vec b )=8 \vec a + 2 \vec b</math><br> | ||
| + | c) <math>-[\vec a - \vec b -(-\vec c )]=-\vec a + \vec b - \vec c</math><br> | ||
| + | d) <math>-3\vec a + [(\vec b - \vec a )-(5\vec a - 3 \vec b )]=-9\vec a + 4 \vec b</math><br> | ||
| + | e) <math> 4\vec b - \vec a -(-2\vec b )=- \vec a + 6 \vec b = 6\vec b - \vec a</math> <br> | ||
| + | f) <math>2(\vec c - \vec a ) - (\vec c - \vec b)=-2\vec a + \vec b + \vec c</math> | ||
| + | |||
| + | Natürlich kann man die Ergebnisse auch in einer anderen Reihenfolge unter Berücksichtigung der Vor-/Rechenzeichen schreiben! Bei e) habe ich es gemacht.}} | ||
| + | |||
| + | Buch S. 98 / 5 | ||
| + | |||
| + | {{Lösung versteckt|1=Hier muss man koordinatenweise rechnen. <br> | ||
| + | a) <math>x \cdot \left ( \begin{array}{c} 2 \\\ 4 \end{array}\right) = \left ( \begin{array}{c} 3 \\\ 6 \end{array}\right)</math> liefert zwei Gleichungen x · 2 = 3 und x · 4 = 6. Beide Gleichungen sind für x = 1,5 richtig. <br> | ||
| + | b) Die zwei Koordinatengleichungen lauten x<sub>1</sub> · 5 = 0 und x</sub>2>/sub> · 1 = 0. Die Gleichungen sind für x<sub>1</sub> = 0 und x<sub>2</sub> = 0 richtig. <br> | ||
| + | c) Die drei Koordinatengleichungen lauten x<sub>1</sub> + 1 = 2, x<sub>2</sub> - 2 = -3 und x<sub>3</sub> + 3 = 0. Die Gleichungen sind jeweils richtig für x<sub>1</sub> = 1, x<sub>2</sub> = -1, x<sub>3</sub> = -3.<br> | ||
| + | d) Die drei Koordinatengleichungen lauten 4 = x·(-2), -8 = x·4, 12 = x·(-6). Alle drei Gleichungen sind für x = -2 richtig.<br> | ||
| + | e) Man kann die rechte Seite der Gleichung vereinfachen, indem man x ausklammert. <math> x\cdot \left ( \begin{array}{c} -1 \\\ 5 \\\ -6 \end{array}\right) + x \cdot \left ( \begin{array}{c} -3 \\\ 7 \\\ -10 \end{array}\right) = x \cdot \left [ \left ( \begin{array}{c} -1 \\\ 5 \\\ -6 \end{array}\right) + \left ( \begin{array}{c} -3 \\\ 7 \\\ -10 \end{array}\right) \right] = x \cdot \left ( \begin{array}{c} -4 \\\ 12 \\\ -16 \end{array}\right) </math> | ||
| + | Die drei Koordinatengleichungen lauten 2 = x·(-4), -6 = x·12, 8 = x·-16. Alle drei Gleichungen sind für x = -0,5 richtig. }} | ||
| + | |||
| + | Buch S. 98 / 7 | ||
| + | |||
| + | {{Lösung versteckt|1=a) <math>\vec a = \left ( \begin{array}{c} 4 \\\ -3 \end{array}\right), \vec b = \left ( \begin{array}{c} 9 \\\ 3 \end{array}\right), \vec c = \left ( \begin{array}{c} -9 \\\ 3 \end{array}\right), \vec d = \left ( \begin{array}{c} -4 \\\ -3 \end{array}\right)</math> <br> | ||
| + | <math>\vec a + \vec b + \vec c + \vec d = \left ( \begin{array}{c} 4 \\\ -3 \end{array}\right) + \left ( \begin{array}{c} 9 \\\ 3 \end{array}\right) + \left ( \begin{array}{c} -9 \\\ 3 \end{array}\right) + \left ( \begin{array}{c} -4 \\\ -3 \end{array}\right) = \left ( \begin{array}{c} 0 \\\ 0 \end{array}\right)</math><br> | ||
| + | Wenn man der Reihe nach die Vektoren aneinandersetzt kommt man wieder an den Punkt A, der Summenvektor <math>\vec a + \vec b + \vec c + \vec d </math> ist also der Vektore <math>\vec {AA} = \vec o</math>. | ||
| + | |||
| + | b) <math>\vec {AC} = \left ( \begin{array}{c} 13 \\\ 3 \end{array}\right) - \left ( \begin{array}{c} 0 \\\ 3 \end{array}\right) = \left ( \begin{array}{c} 13 \\\ 0 \end{array}\right) </math> (das ist die waagrechte Diagonale von A nach C)<br> | ||
| + | <math>\vec {BD} = \left ( \begin{array}{c} 4 \\\ 6 \end{array}\right) - \left ( \begin{array}{c} 4 \\\ 0 \end{array}\right) = \left ( \begin{array}{c} 0 \\\ 6 \end{array}\right)</math> (das ist die senkrechte Diagonale von B nach D) | ||
| + | |||
| + | c) Der gesuchte Punkt ist der Schnittpunkt der Winkelhalbierenden des Winkels BAD mit der Winkelhalbierenden des Winkels ADC.}} | ||
| + | }} | ||
Aktuelle Version vom 10. Januar 2021, 10:27 Uhr
Man kann mit Vektoren auch rechnen. Es gibt zwei Rechenarten für Vektoren, die Addition und die S-Mulitplikation.
30px Merke
Addition von Vektoren |
Rechnerisch heißt das, dass man die Koordinaten der Vektoren addiert, man spricht von koordinatenweiser Addition.
Für die Vektoren 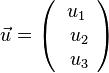 und
und 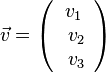 gilt dann für den Summenvektor
gilt dann für den Summenvektor 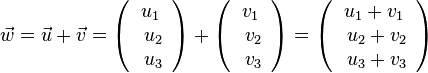 .
.
Die Koordinaten des Summenvektors sind die Summen der Koordinaten der Summanden.
Beispiele: 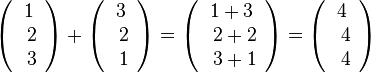
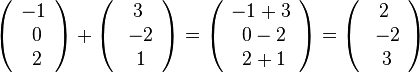
Für die Vektoraddition gelten auch Rechengesetze. Aus der Algebra kennt man für das Rechnen mit Buchstaben das Kommutativgesetz und das Assoziativgesetz. Diese Gesetze gelten auch für Vektoren. Das Kommutativgesetz sieht man sehr einfach bei der Konstruktion des Summenvektors: Datei:Wektory sumr.svg
Vektor 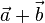 führt zum selben Ergebnis wie
führt zum selben Ergebnis wie 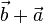 .
.
Das Assoziativgesetz für Vektoren kann man in diesem Applet nachvollziehen.
Verändert man die Vektoren 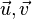 oder
oder 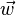 so ergibt sich stets der gleiche schwarze Pfeil als
so ergibt sich stets der gleiche schwarze Pfeil als 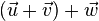 oder
oder 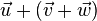 .
.
Vektoren eignen sich prina für Wege von A nach B. Macht man einen Umweg über C, dann gehe entlang der Vektoren 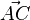 und
und 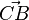 , also gehe mit dem Summenvektor
, also gehe mit dem Summenvektor 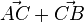 .
.
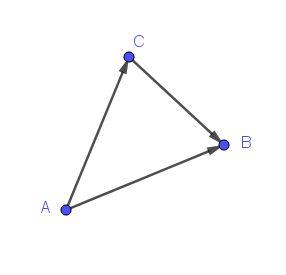
Um von A über C nach B zu kommen kann man aber auch statt 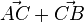 eine Abkürzung nehmen, nämlich
eine Abkürzung nehmen, nämlich 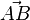 .
.
1a) 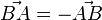
b) 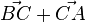
2a) 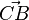
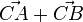
30px Merke
S-Multiplikation Durch Ziehen am Schieberegler verändert man den Wert von c. Der rote Vektor Jede Koordinate des Vektors |
Beispiele: 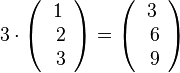
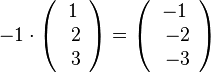 Beachte:
Beachte: 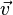 ist der Gegenvektor zu
ist der Gegenvektor zu 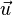 .
.
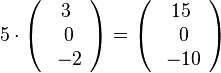
30px Merke
Man sieht, dass das Rechnen mit Vektoren genauso geht wie das Rechnen in der Algebra mit Buchstaben und Zahlen, nur dass nun über den Buchstaben noch ein Vektorpfeil istl. Es gibt die Vektoraddition mit der man Vektoren addieren kann und die S-Multiplikation, bei der Vektoren mit reellen Zahlen multipliziert werden. Das geht genauso wie man es bisher beim Rechnen mit Zahlen und Buchstaben kennengelernt hat. |
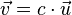 .
. 
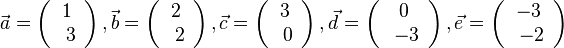
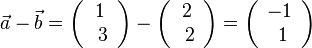
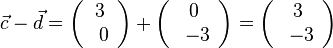
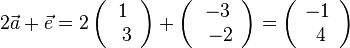
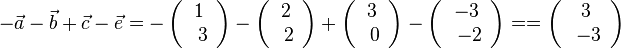
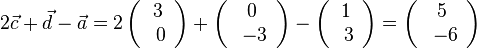
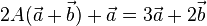
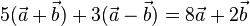
![-[\vec a - \vec b -(-\vec c )]=-\vec a + \vec b - \vec c](/images/math/4/b/a/4bad741133ada5db6e4144e39981117b.png)
![-3\vec a + [(\vec b - \vec a )-(5\vec a - 3 \vec b )]=-9\vec a + 4 \vec b](/images/math/1/8/e/18eaadb5316d0dd34f61e19424d26f7a.png)
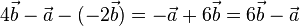
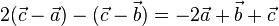
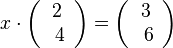 liefert zwei Gleichungen x · 2 = 3 und x · 4 = 6. Beide Gleichungen sind für x = 1,5 richtig.
liefert zwei Gleichungen x · 2 = 3 und x · 4 = 6. Beide Gleichungen sind für x = 1,5 richtig. ![x\cdot \left ( \begin{array}{c} -1 \\\ 5 \\\ -6 \end{array}\right) + x \cdot \left ( \begin{array}{c} -3 \\\ 7 \\\ -10 \end{array}\right) = x \cdot \left [ \left ( \begin{array}{c} -1 \\\ 5 \\\ -6 \end{array}\right) + \left ( \begin{array}{c} -3 \\\ 7 \\\ -10 \end{array}\right) \right] = x \cdot \left ( \begin{array}{c} -4 \\\ 12 \\\ -16 \end{array}\right)](/images/math/7/b/7/7b7264ae1ca7d2fb5ffb81a391088aa8.png)
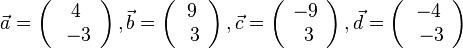
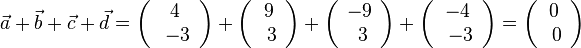
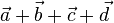 ist also der Vektore
ist also der Vektore 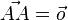 .
.
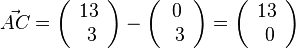 (das ist die waagrechte Diagonale von A nach C)
(das ist die waagrechte Diagonale von A nach C)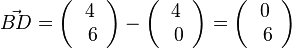 (das ist die senkrechte Diagonale von B nach D)
(das ist die senkrechte Diagonale von B nach D)

