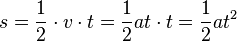Ph9 tx- und tv- Abhängigkeiten: Unterschied zwischen den Versionen

Aus RSG-Wiki
Wechseln zu: Navigation, Suche
 
(12 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 23: Zeile 23:
 
}}
 
}}
  
−
  Die Fläche unter der Kurve im tv-Diagramm ist eine Rechtecksfläche und berechnet sich als v·t.<br>
+
  Die Fläche unter der Kurve im tv-Diagramm ist eine Rechtecksfläche und berechnet sich als v·t.
 
  Sie stellt den zurückgelegten Weg s dar.  
 
  Sie stellt den zurückgelegten Weg s dar.  
  
−
{{Aufgaben-blau|2|2=a) Lies aus den Diagrammen für die Bewegung mit konstanter Geschwindigkeit die Werte für t, v und s ab.<br>
+
{{Aufgaben-blau|2|2=a) Lies aus den Diagrammen für die Bewegung mit konstanter Geschwindigkeit im Merkkasten die Werte für t, v und s ab.<br>
 
b) Gib die Bewegungsgleichung an. }}
 
b) Gib die Bewegungsgleichung an. }}
  
Zeile 58: Zeile 58:
 
<math>s = \frac{1}{2}at^2</math></center>  }}
 
<math>s = \frac{1}{2}at^2</math></center>  }}
  
−
{{Aufgaben-blau|4|2=a) Lies aus den Diagrammen für die Bewegung mit konstanter Beschleunigung die Werte für t, a,  v und s ab.<br>
+
Die Fläche unter der Kurve im tv-Diagramm ist eine Dreiecksfläche und berechnet sich als 0,5·v·t.
 +
Sie stellt den zurückgelegten Weg s dar.
 +
Mit v = a·t ist s=0,5·v·t=0,5·a·t<sup>2</sup>.
 +
 
 +
{{Aufgaben-blau|4|2=a) Lies aus den Diagrammen für die Bewegung mit konstanter Beschleunigung im obigen Merkkasten für die Bewegung mit konstanter Beschleunigung die Werte für t, a,  v und s ab.<br>
 
b) Gib die Bewegungsgleichungen an. }}
 
b) Gib die Bewegungsgleichungen an. }}
  
Zeile 68: Zeile 72:
  
 
  '''Beachte:''' Die Bewegungsgleichung s = v·t darf man nicht bei der Bewegung mit konstanter Beschleunigung verwenden!
 
  '''Beachte:''' Die Bewegungsgleichung s = v·t darf man nicht bei der Bewegung mit konstanter Beschleunigung verwenden!
 +
 +
<center>{{#ev:youtube |Fm0-2GXHTZk|350}}</center>
  
 
{{Aufgaben-blau|5|2=Buch S. 61 / 3, 4, 5  }}
 
{{Aufgaben-blau|5|2=Buch S. 61 / 3, 4, 5  }}
Zeile 79: Zeile 85:
 
61/4 <ggb_applet height="500" width="700"
 
61/4 <ggb_applet height="500" width="700"
 
filename="61-4.ggb" />
 
filename="61-4.ggb" />
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
  
 
Bei a) und c) jeweils gleiche Zeiten, bei b) und d) gleiche Strecken!
 
Bei a) und c) jeweils gleiche Zeiten, bei b) und d) gleiche Strecken!
Zeile 86: Zeile 117:
 
Man kann nicht gleichzeitig an zwei verschiedenen Orten sein.
 
Man kann nicht gleichzeitig an zwei verschiedenen Orten sein.
 
}}
 
}}
 +
 +
{{Aufgaben-blau|6|2=1. Schaue dir das Applet [https://www.leifiphysik.de/mechanik/lineare-bewegung-gleichungen/grundwissen/zeit-orts-diagramm auf dieser Seite] zur Entstehung eines Zeit-Ort-Diagramms an und erkläre was ein ts-Diagramm ist. <br>
 +
2. Buch S. 65 / 1, 2 }}
 +
 +
{{Lösung versteckt|1=1. In einem ts-Diagramm werden Zeit-Ort-Wertepaaren (t,s) dargestellt. Für jedes t im Zeitintervall wird der entsprechende Ort darüber aufgetragen, dabei wird die Zeit nach rechts und der Weg nach oben angetragen.<br>
 +
 +
2. S.65/1 Zugrunde liegt das th-Diagramm Bild 5 auf S. 65. <br>
 +
a) Nach 17s ist der Fahrstuhl in der Höhe h = 31m,<br>
 +
b) Bei t = 7,5s und t = 15,8s ist der Fahrstuhl bei h = 42m.<br>
 +
c) (3s,12m), (9s,51m) hat <math>\Delta</math>h=39m.<br>
 +
In dem Intervall [3s,9s] ist der Graph eine Gerade, daher stimmt Momentangeschwindigkeit mit Durchschnittsgeschwindigkeit überein.<br>
 +
d) (9s, 51m), (11s,60m); <math>\Delta</math>h=9m und <math>v_D=\frac{\Delta h }{\Delta t}=\frac{9m}{2s}=4,5\frac{m}{s}</math><br>
 +
e) Die Fahrt ist am schnellsten wo der Graph am steilsten ist (am steilsten kann auch der fallende Teil ab 14s sein.) Man legt das Geodreieck entlang des Graphen an und erkennt, dass es am steilsten t = 18,8s und t = 20s ist.<br>
 +
Die Plattform ist in Ruhe für 11s ≤ t ≤ 13,9s und 17,2s ≤ t ≤17,8s.<br>
 +
f) Graph waagrecht: es gibt keine Ortsänderungs, der Fahrstuhl ist in Ruhe<br>
 +
Graph geradlinig ansteigend: der Fahrstuhl fährt mit konstanter Geschwindigkeit hoch<br>
 +
Graph geradlinig absteigend: der Fahrstuhl fährt mit konstanter Geschwindigkeit runter<br>
 +
g) Graph steiler: Momentangeschwindigkeit wird größer<br>
 +
Graph flacher: Momentangeschwindigkeit wird kleiner
 +
 +
S.65/2<br>
 +
[[Datei:65-2.jpg|800px]]<br>
 +
Die Punkte verbindet man im Heft, indem man sich das Heft so hinlegt, dass man mit einem Strich "aus dem Handgelenk" die Punkte <br> schön verbinden kann. Es sollen nicht Punkte miteinander verbunden werden, sondern es soll eine glatte Kurve ergeben.<br>
 +
b) Bei y = 1m geht man waagrecht nach rechts bis man den Graph trifft. Im Treffpunkt geht man dann senkrecht nach unten und liest auf der t-Achse t = 0,31 s ab.<br>
 +
c) Bei t = 0,15s geht man senkrecht nach oben bis man den Graph trifft. Im Treffpunkt geht man dann waagrecht nach links und liest auf der y-Achse y = 140m ab.<br>
 +
Verlängert man den Graph nach rechts bis man er die t-Achse trifft, dann schneidet er sie bei t=0,53 s.
 +
d)<br>
 +
[[Datei:65-2d 2.jpg]]<br>
 +
Man hat für die 0,1s-Intervalle die Durchschnittsgeschwindigkeit berechnet. Dies bedeutet, dass man in diesem Intervall mit konstanter Geschwindigkeit, eben dieser Durchschnittsgeshwindigkeit, fährt. Daher ergibt sich im Graph so eine Treppenfunktion. <br>
 +
e) Es ist Beschleunigung <math>a = \frac{\Delta v}{\Delta t}</math>.<br>
 +
<math>a_1=\frac{150cm/s - 50 cm/s}{0,1}= \frac{100cm/s}{0,1s}=1000 \frac{cm}{s^2}=10 \frac{m}{s^2}</math><br>
 +
<math>a_2=\frac{350cm/s - 50 cm/s}{0,3}= \frac{300cm/s}{0,3s}=1000  \frac{cm}{s^2}=10 \frac{m}{s^2}</math><br>
 +
<math>a_3=\frac{350cm/s - 250 cm/s}{0,1}= \frac{100cm/s}{0,1s}=1000  \frac{cm}{s^2}=10 \frac{m}{s^2}</math><br>
 +
Egal welche Kombination man wählt es kommt immer a = 10m/s² heraus.<br>
 +
f) Aus c) weiß man t = 0,53s Er wird mit einer Geschwindigkeit 480 cm/s aufkommen (Dreisatz).  }}
 +
 +
{{Aufgaben-blau|7|2=Bearbeite <br>
 +
1. [https://www.leifiphysik.de/mechanik/lineare-bewegung-gleichungen/aufgabe/quiz-zu-zeit-orts-diagrammen das Quiz zu Zeit-Ort-Diagramm ]<br>
 +
2. [https://www.leifiphysik.de/mechanik/lineare-bewegung-gleichungen/aufgabe/reisezeiten die Aufgabe zu Reisezeiten] }}
 +
 +
{{Aufgaben-blau|8|Buch S. 68 / 4, 5}}
 +
 +
{{Lösung versteckt|1=68/4a) Schaut man zuerst das tx-Diagramm an, so sieht man, dass bis 0,2s der Bogen fast nicht bewegt wird, dann wird bis 0,4s gestrichen, der Bogen legt Weg zurück. Von 0,4s bis 0,8s bleibt der Bogen ziemlich in Ruhe bevor er dann bis 1,1s weiter bewegt wird. Ab 1,1s ist er wieder ziemlich ohne Bewegung bis 1,7s. Danach nimmt der Weg ab, d.h. der Bogen geht zurück und zwar ziemlich gleichmäßig bis 3,2s. Von 3,2s bis 3,4s wird der Bogen noch einmal schneller bewegt und geht über die Anfangslange hinaus bis er dann ab 3,4s in Ruhe ist.<br>
 +
Die gerade eben beschriebene Bewegung sollte im tv-Diagramm erkennbar sein. Wenn der Bogen in Ruhe ist, dann ist seine Geschwindigkeit fast 0m/s, wenn er schnell bewegt wird, dann ist seine Geschwindigkeit groß, wenn er zurück bewegt wird ist die Geschwindigkeit negativ, da die Richtung durch das Vorzeichen angezeigt wird.<br>
 +
Bis 0,2s hat der Bogen wenig Weg zurück gelegt, seine Geschwindigkeit ist fast 0m/s, dann von 0,2s bis 0,4s wird der schnell bewegt, die Geschwindigkeit nimmt bis zum wert 1m/s zu um dann gleich wieder bis 0,6s langsamer zu werden und in Ruhe zu sein. Ab 0,8s wird der bogen wieder schneller werden gestrichen bis bei 1,0s die Maximalgeschwindigkeit erreicht ist und danach bis 1,2s wieder abnimmt um danach bis 1,7s in Ruhe zu sein. Danach wird der Bogen zurück bewegt, zuerst mit größer werdender Geschwindigkeit bis 1,8s, dann bis 2,2s wieder langsamer werdend  und ab 2,2s mit konstanter langsamer Geschwindigkeit bis 3,0s. Ab 3,0s wird der Bogen wieder schneller bewegt bis 3,4s und danach bis 3,6s langsamer werdend zur Ruhe kommend.<br>
 +
Die Zeitwerte passen nicht immer genau zusammen, der große Trend ist aber immer erkennbar. Wenn die Geschwindigkeit im tv-Diagram am höchsten ist, dann ist der Weg im tx-Diagramm am steilsten. Wenn im tx-Diagramm der Weg nicht zunimmt, dann ist im tv-Diagramm die Geschwindigkeit auch (fast) 0m/s.<br>
 +
b) Wenn die Lautstärke von der Geschwindigkeit des Bogens abhängt, dann nimmt die Lautstärke auch entsprechend dem tv-Diagramm zu und ab. Allerdings wenn die Geschwindigkeit negativ wird, dann wird die Lautstärke '''nicht''' negativ. Was sollte auch eine negative Lautstärke sein? Dann spiegelt man den negativen Teil des tv-Diagramms an der t-Achse nach oben und hat dann den Lautstärkeverlauf.<br>
 +
c) Die Dreiecksfläche ist <math>A=\frac{1}{2}gh</math>. mit g = 0,6s und h = 1m/s ergibt sich A = 0,3m = 30cm. Das ist der Weg, den der Bogen nach 0,6s erreicht hat.
 +
 +
68/5 a) Der Beschleunigungsvorgang von v<sub>1</sub>=150km/h auf v<sub>2</sub>=180km/h dauert 28s. <math>v_1=150\frac{km}{h}=41\frac{2}{3}\frac{m}{s}</math> und <math>v_2=180\frac{km}{h}=50\frac{m}{s}</math>. Also ist <math>E_{kin,1}=0,5\cdot 1500kg \cdot (41\frac{2}{3}\frac{m}{s})^2=1,302MJ</math> und <math>E_{kin,2}=0,5\cdot 1500kg \cdot (50\frac{m}{s})^2=1,875MJ</math>. Die kinetische Energie nimmt um 0,573MJzu.<br>
 +
Die Motorleistung ist <math>P=\frac{\Delta E_{kin}}{\Delta t}=\frac{0,573MJ}{28s}=20,5kW</math><br>
 +
Bei der Beschleunigung von 0m/s auf <math>90\frac{km}{h}=25\frac{m}{s}</math> bekommt der Wagen die kinetische Energie <math>E_{kin}=0,5\cdot 1500kg\cdot (25\frac{m}{s})^2=0,469MJ</math>. Der Vorgang dauert 9s und die Motorleistung ist <math>P=\frac{\Delta E_{kin}}{\Delta t}=\frac{0,469MJ}{9s}=52,1kW</math>, also deutlich mehr als dooppelt so groß als beim Beschleunigen bei hohen Geschwindigkeiten.<br>
 +
b) Der Zacken am Anfang entsteht durch den Schaltvorgang. Man tritt die Kupplung und schaltet. Während dieser Zeit wirkt keine Motorkraft, die Geschwindigkeit nimmt ab. Nach dem Schalten in den nächsten Gang wirkt wieder die Motorkraft und der Wagen beschleunigt weiter. Dies macht sich bei kleinen Geschwindigkeiten stärker bemerkbar als bei größeren Geschwindigkeiten.  }}
 +
 +
{{Aufgaben-blau|9|2=Buch S. 71 / 1, <br>
 +
Buch S. 71 / 2, {{#ev:youtube |z2uJioNMl-I|350}}<br>
 +
Buch S. 71 / 3}}
 +
 +
{{Lösung versteckt|1=71/1 Ein Flugzeug fliegt mit konstanter Geschwindigkeit, daher ist <math>v=\frac{\Delta x}{\Delta t}</math>. Mit den angegebenen Werten berechnet man <math>\Delta t=\frac{\Delta x}{v}=\frac{3337km}{1020\frac{km}{h}}=3,27h</math><br>
 +
Es ist gerade 15:02 Uhr
 +
 +
71/2 a) Es ist <math>v=80\frac{km}{h}=22,2\frac{m}{s}</math>. Mit dieser konstanten Geschwindigkeit legt man in 5s die Strecke 111m zurück. <br>
 +
Allerdings hat man bei dem Fahrgeschäft keine Bewegung mit konstanter Geschwindigkeit, sondern oben ist die Geschwindigkeit 0 und nach dem Losfahren hat man eine Bewegung mit konstanter Beschleunigung. Für die beschleunigte Bewegung ist <math>s = 0,5g t^2</math>. Nimmt man s = 70m, dann ist <math>t=\sqrt {\frac{2s}{g}}=\sqrt {\frac{2\cdot 70m}{9,8\frac{m}{s^2}}}=3,8s</math>. Dabei erreicht man die Geschwindigkeit <math>v=gt=9,8\frac{m}{s^2}\cdot 3,8s=37\frac{m}{s}=134\frac{km}{h}</math>.<br>
 +
Die Durchschnittsgeschwindigkeit ist <math>v_D=\frac{\Delta x}{\Delta t}=\frac{70m}{3,8s}=18\frac{m}{s}=65\frac{km}{h}</math>.<br>
 +
Beachte, dass du für eine beschleunigte Bewegung '''nicht''' s = vt verwenden darfst, sondern du musst <math>s=\frac{1}{2}at^2</math> nehmen.
 +
 +
 +
Die gegebenen Daten in der Aufgabe s = 70m, t = 5s und v = 80km/h passen nicht zusammen. Die Höhe s des Turms ist gegeben, da kann man nichts ändern, die Zeit t lässt sich leicht mit einer Uhr messen. Einen Geschwindigkeitsmesser hat man normal nicht dabei.
 +
Nimmt man eine Bewegung mit konstanter Geschwindigkeit an, dann ist die Geschwindigkeit <math>v=\frac{70m}{5s}=14\frac{m}{s}=50,4\frac{km}{h}</math>, also passt die Aussage 80km/h nicht.<br>
 +
Nimmt man eine beschleunigte Bewegung, dann hat man oben für die Fallzeit t = 3,8s berechnet. Gut, die Sitze müssen auch noch abgebremst werden, so dass man auf 5s kommen kann. Die Abbremsung erfolgt vielleicht auf den letzten 10m. Dann ist die Fallzeit 3,5s und die erreichte Höchstgeschwindigkeit <math>v=9,8\frac{m}{s^2}\cdot 3,5s=34,3\frac{m}{s}=132\frac{km}{h}</math>, passt also auch nicht. <br>
 +
Nimmt man für die Durchschnittsgeschwindigkeit <math>v_D=\frac{70m}{5s}=14\frac{m}{s}=50,4\frac{km}{h}</math>, passt also auch nicht.
 +
 +
71/3 a) Du fährst mit konstanter Geschwindigkeit <math>v=\frac{s}{t}</math>, dann ist <math>t=\frac{s}{v}=\frac{1,6km}{24\frac{km}{h}}=0,06666h=4min</math>. Du erreichst die Schule in 4 Minuten.<br>
 +
b) Um schon in 3 Minuten an der Schule zu sein, musst du schneller fahren, also beschleunigen und dann mit größerer konstanter Geschwindigkeit weiterfahren. Dies kann z.b. passieren, wenn es bergab geht. }}

Aktuelle Version vom 8. Februar 2021, 18:04 Uhr

Ihr habt schon zwei Arten von Bewegungen kennengelernt:

  • Bewegung mit konstanter Geschwindigkeit und
  • Bewegung mit konstanter Beschleunigung

Für beide Bewegungen sammeln wir zuerst unsere bisherigen Kenntnisse:

1. Gleichförmige Bewegung:


Bleistift 35fach.jpg   Aufgabe 1

Schaue dir dies Video an und notiere die Fakten

Nuvola apps kig.png   Merke

Bei einer gleichförmigen Bewegung bewegt sich ein Körper geradlinig mit konstanter Geschwindigkeit v = konstant.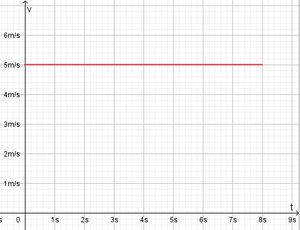
Im tv-Diagramm wird nach rechts die Zeit t und nach oben die Geschwindigkeit v aufgetragen.

Tv-diagramm.jpg

Im ts-Diagramm wird auch nach rechts die Zeit t aber nach oben der zurückgelegte Weg s aufgetragen.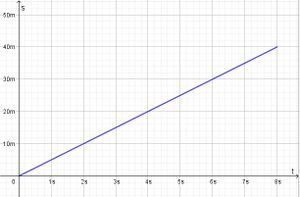

Ts-Diagramm.jpg

Die Strecke beginnt im Ursprung und steigt linear an.

Formeln:

v = konstant

s=v\cdot t

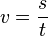v = \frac{s}{t}
Die Fläche unter der Kurve im tv-Diagramm ist eine Rechtecksfläche und berechnet sich als v·t.
Sie stellt den zurückgelegten Weg s dar.


Bleistift 35fach.jpg   Aufgabe 2

a) Lies aus den Diagrammen für die Bewegung mit konstanter Geschwindigkeit im Merkkasten die Werte für t, v und s ab.
b) Gib die Bewegungsgleichung an.

a) Die Bewegung verläuft für 0s ≤ t ≤ 8s ab.
v = 5 m/s
Der insgesamt zurückgelegte Weg ist s = 40m.

b) s = 5m/s ·t


2. Gleichmäßig beschleunigte Bewegung:


Bleistift 35fach.jpg   Aufgabe 3

Schaue dir dies Video an und notiere die Fakten

Nuvola apps kig.png   Merke

Bei einer gleichmäßig beschleunigten Bewegung bewegt sich ein Körper geradlinig und wird mit konstanter Beschleunigung beschleunigt.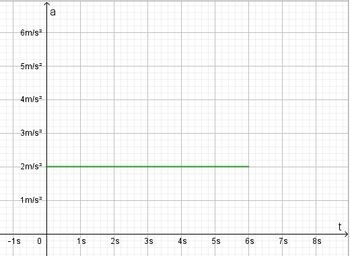
a = konstant
Im ta-Diagramm wird nach rechts die Zeit t und nach oben die Beschleunigung a aufgetragen.

Ta-diagramm 2.jpg

Im tv-Diagramm wird nach rechts die Zeit t und nach oben die Geschwindigkeit v aufgetragen.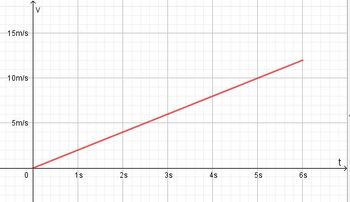

Tv-diagramm 2.jpg

Beschleunigung a=\frac{\Delta v}{\Delta t} , da a konstant ist gilt auch a = \frac{v}{t}.
Die Fläche unter dem Graph im ta-Diagramm stellt die Geschwindigkeit v dar. Es ist v = a \cdot t.
Im ts-Diagramm wird nach rechts die Zeit t und nach oben der zurückgelegte Weg s aufgetragen.

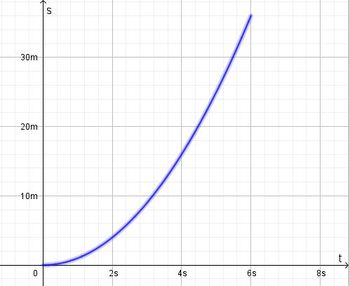Ts-Diagramm 2.jpg

Auch hier stellt die Fläche unter dem Graph im tv-Diagramm den zurückgelegtn Weg s dar. Es ist s=\frac{1}{2}\cdot v\cdot t = \frac{1}{2} at\cdot t=\frac{1}{2} at^2

Formeln:

a = konstant

v = a \cdot t oder a = \frac{v}{t}

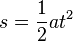s = \frac{1}{2}at^2
Die Fläche unter der Kurve im tv-Diagramm ist eine Dreiecksfläche und berechnet sich als 0,5·v·t.
Sie stellt den zurückgelegten Weg s dar. 
Mit v = a·t ist s=0,5·v·t=0,5·a·t2.


Bleistift 35fach.jpg   Aufgabe 4

a) Lies aus den Diagrammen für die Bewegung mit konstanter Beschleunigung im obigen Merkkasten für die Bewegung mit konstanter Beschleunigung die Werte für t, a, v und s ab.
b) Gib die Bewegungsgleichungen an.

a) Die Bewegung verläuft für 0s ≤ t ≤ 6s ab.
a=2m/s²
Die mach 6s erreichte Geschwindigkeit ist v = 12 m/s
Der insgesamt zurückgelegte Weg ist s = 36m.

b) v = 2m/s² ·t, s = 0,5·2m/s²·t²
Beachte: Die Bewegungsgleichung s = v·t darf man nicht bei der Bewegung mit konstanter Beschleunigung verwenden!


Bleistift 35fach.jpg   Aufgabe 5

Buch S. 61 / 3, 4, 5

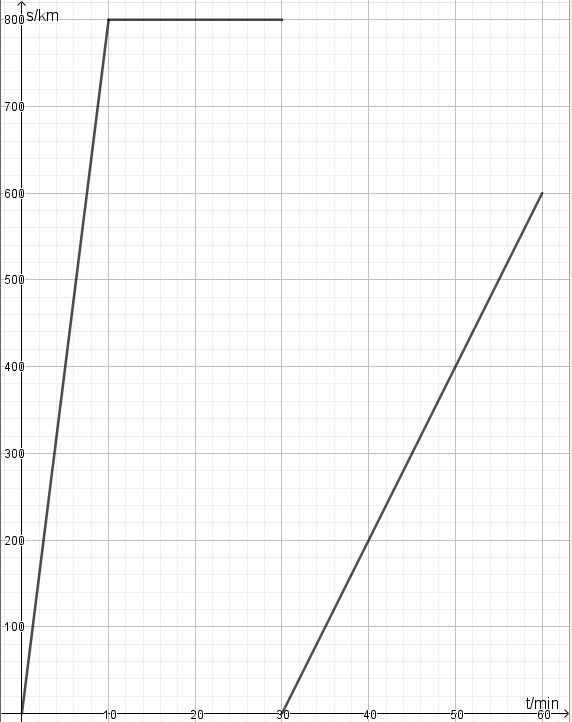
61/3 Es handelt sich um Bewegungen mit konstanter Geschwindigkeit. Im ts-Diagramm sind das Geraden. Die Geschwindigkeit gibt die Steigung der Geraden an. Je steiler die Gerade, desto größer ist die Geschwindigkeit.
a) Zeit bergab ist genauso lang wie Zeit bergauf (t-Achse), bergab steiler als bergauf --> Diagramm III
b) Strecke bergauf ist genauso lang wie Strecke bergab (s-Achse), bergauf nicht so steil wie bergab ---> Diagramm II
c) Zeit bergauf ist genauso lang wie Zeit bergab (t-Achse), bergauf nicht so steil wie bergab ---> Diagramm IV
d) Strecke bergab ist genauso lang wie Strecke bergauf (s-Achse), bergab steiler als bergauf ---> Diagramm I

61/4














Bei a) und c) jeweils gleiche Zeiten, bei b) und d) gleiche Strecken!

61/5
61-5.jpg

Man kann nicht gleichzeitig an zwei verschiedenen Orten sein.


Bleistift 35fach.jpg   Aufgabe 6

1. Schaue dir das Applet auf dieser Seite zur Entstehung eines Zeit-Ort-Diagramms an und erkläre was ein ts-Diagramm ist.
2. Buch S. 65 / 1, 2

1. In einem ts-Diagramm werden Zeit-Ort-Wertepaaren (t,s) dargestellt. Für jedes t im Zeitintervall wird der entsprechende Ort darüber aufgetragen, dabei wird die Zeit nach rechts und der Weg nach oben angetragen.

2. S.65/1 Zugrunde liegt das th-Diagramm Bild 5 auf S. 65.
a) Nach 17s ist der Fahrstuhl in der Höhe h = 31m,
b) Bei t = 7,5s und t = 15,8s ist der Fahrstuhl bei h = 42m.
c) (3s,12m), (9s,51m) hat 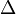\Deltah=39m.
In dem Intervall [3s,9s] ist der Graph eine Gerade, daher stimmt Momentangeschwindigkeit mit Durchschnittsgeschwindigkeit überein.
d) (9s, 51m), (11s,60m); 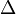\Deltah=9m und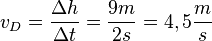 v_D=\frac{\Delta h }{\Delta t}=\frac{9m}{2s}=4,5\frac{m}{s}
e) Die Fahrt ist am schnellsten wo der Graph am steilsten ist (am steilsten kann auch der fallende Teil ab 14s sein.) Man legt das Geodreieck entlang des Graphen an und erkennt, dass es am steilsten t = 18,8s und t = 20s ist.
Die Plattform ist in Ruhe für 11s ≤ t ≤ 13,9s und 17,2s ≤ t ≤17,8s.
f) Graph waagrecht: es gibt keine Ortsänderungs, der Fahrstuhl ist in Ruhe
Graph geradlinig ansteigend: der Fahrstuhl fährt mit konstanter Geschwindigkeit hoch
Graph geradlinig absteigend: der Fahrstuhl fährt mit konstanter Geschwindigkeit runter
g) Graph steiler: Momentangeschwindigkeit wird größer
Graph flacher: Momentangeschwindigkeit wird kleiner

S.65/2
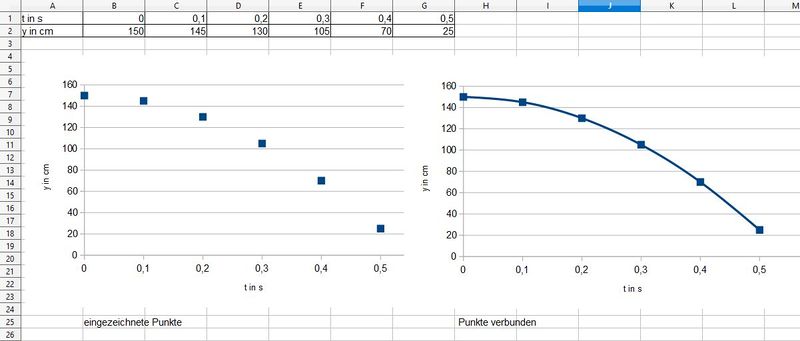
65-2.jpg

Die Punkte verbindet man im Heft, indem man sich das Heft so hinlegt, dass man mit einem Strich "aus dem Handgelenk" die Punkte 
 schön verbinden kann. Es sollen nicht Punkte miteinander verbunden werden, sondern es soll eine glatte Kurve ergeben.

b) Bei y = 1m geht man waagrecht nach rechts bis man den Graph trifft. Im Treffpunkt geht man dann senkrecht nach unten und liest auf der t-Achse t = 0,31 s ab.
c) Bei t = 0,15s geht man senkrecht nach oben bis man den Graph trifft. Im Treffpunkt geht man dann waagrecht nach links und liest auf der y-Achse y = 140m ab.
Verlängert man den Graph nach rechts bis man er die t-Achse trifft, dann schneidet er sie bei t=0,53 s. d)
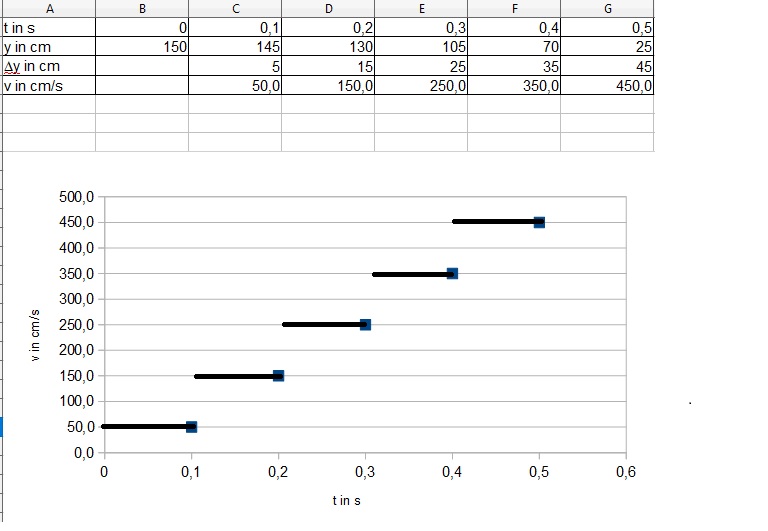
65-2d 2.jpg
Man hat für die 0,1s-Intervalle die Durchschnittsgeschwindigkeit berechnet. Dies bedeutet, dass man in diesem Intervall mit konstanter Geschwindigkeit, eben dieser Durchschnittsgeshwindigkeit, fährt. Daher ergibt sich im Graph so eine Treppenfunktion.
e) Es ist Beschleunigung 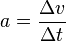a = \frac{\Delta v}{\Delta t}.
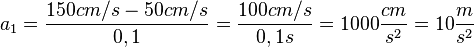
a_1=\frac{150cm/s - 50 cm/s}{0,1}= \frac{100cm/s}{0,1s}=1000 \frac{cm}{s^2}=10 \frac{m}{s^2}
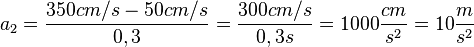
a_2=\frac{350cm/s - 50 cm/s}{0,3}= \frac{300cm/s}{0,3s}=1000 \frac{cm}{s^2}=10 \frac{m}{s^2}
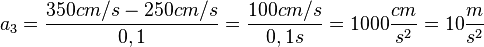
a_3=\frac{350cm/s - 250 cm/s}{0,1}= \frac{100cm/s}{0,1s}=1000 \frac{cm}{s^2}=10 \frac{m}{s^2}
Egal welche Kombination man wählt es kommt immer a = 10m/s² heraus.

f) Aus c) weiß man t = 0,53s Er wird mit einer Geschwindigkeit 480 cm/s aufkommen (Dreisatz).


Bleistift 35fach.jpg   Aufgabe 7


Bleistift 35fach.jpg   Aufgabe 8

Buch S. 68 / 4, 5

68/4a) Schaut man zuerst das tx-Diagramm an, so sieht man, dass bis 0,2s der Bogen fast nicht bewegt wird, dann wird bis 0,4s gestrichen, der Bogen legt Weg zurück. Von 0,4s bis 0,8s bleibt der Bogen ziemlich in Ruhe bevor er dann bis 1,1s weiter bewegt wird. Ab 1,1s ist er wieder ziemlich ohne Bewegung bis 1,7s. Danach nimmt der Weg ab, d.h. der Bogen geht zurück und zwar ziemlich gleichmäßig bis 3,2s. Von 3,2s bis 3,4s wird der Bogen noch einmal schneller bewegt und geht über die Anfangslange hinaus bis er dann ab 3,4s in Ruhe ist.
Die gerade eben beschriebene Bewegung sollte im tv-Diagramm erkennbar sein. Wenn der Bogen in Ruhe ist, dann ist seine Geschwindigkeit fast 0m/s, wenn er schnell bewegt wird, dann ist seine Geschwindigkeit groß, wenn er zurück bewegt wird ist die Geschwindigkeit negativ, da die Richtung durch das Vorzeichen angezeigt wird.
Bis 0,2s hat der Bogen wenig Weg zurück gelegt, seine Geschwindigkeit ist fast 0m/s, dann von 0,2s bis 0,4s wird der schnell bewegt, die Geschwindigkeit nimmt bis zum wert 1m/s zu um dann gleich wieder bis 0,6s langsamer zu werden und in Ruhe zu sein. Ab 0,8s wird der bogen wieder schneller werden gestrichen bis bei 1,0s die Maximalgeschwindigkeit erreicht ist und danach bis 1,2s wieder abnimmt um danach bis 1,7s in Ruhe zu sein. Danach wird der Bogen zurück bewegt, zuerst mit größer werdender Geschwindigkeit bis 1,8s, dann bis 2,2s wieder langsamer werdend und ab 2,2s mit konstanter langsamer Geschwindigkeit bis 3,0s. Ab 3,0s wird der Bogen wieder schneller bewegt bis 3,4s und danach bis 3,6s langsamer werdend zur Ruhe kommend.
Die Zeitwerte passen nicht immer genau zusammen, der große Trend ist aber immer erkennbar. Wenn die Geschwindigkeit im tv-Diagram am höchsten ist, dann ist der Weg im tx-Diagramm am steilsten. Wenn im tx-Diagramm der Weg nicht zunimmt, dann ist im tv-Diagramm die Geschwindigkeit auch (fast) 0m/s.
b) Wenn die Lautstärke von der Geschwindigkeit des Bogens abhängt, dann nimmt die Lautstärke auch entsprechend dem tv-Diagramm zu und ab. Allerdings wenn die Geschwindigkeit negativ wird, dann wird die Lautstärke nicht negativ. Was sollte auch eine negative Lautstärke sein? Dann spiegelt man den negativen Teil des tv-Diagramms an der t-Achse nach oben und hat dann den Lautstärkeverlauf.
c) Die Dreiecksfläche ist 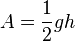A=\frac{1}{2}gh. mit g = 0,6s und h = 1m/s ergibt sich A = 0,3m = 30cm. Das ist der Weg, den der Bogen nach 0,6s erreicht hat.

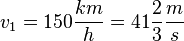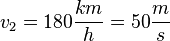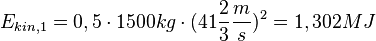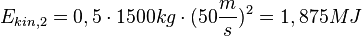68/5 a) Der Beschleunigungsvorgang von v1=150km/h auf v2=180km/h dauert 28s. v_1=150\frac{km}{h}=41\frac{2}{3}\frac{m}{s} und v_2=180\frac{km}{h}=50\frac{m}{s}. Also ist E_{kin,1}=0,5\cdot 1500kg \cdot (41\frac{2}{3}\frac{m}{s})^2=1,302MJ und E_{kin,2}=0,5\cdot 1500kg \cdot (50\frac{m}{s})^2=1,875MJ. Die kinetische Energie nimmt um 0,573MJzu.
Die Motorleistung ist 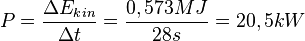P=\frac{\Delta E_{kin}}{\Delta t}=\frac{0,573MJ}{28s}=20,5kW
Bei der Beschleunigung von 0m/s auf 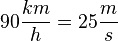90\frac{km}{h}=25\frac{m}{s} bekommt der Wagen die kinetische Energie 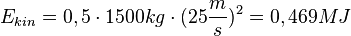E_{kin}=0,5\cdot 1500kg\cdot (25\frac{m}{s})^2=0,469MJ. Der Vorgang dauert 9s und die Motorleistung ist 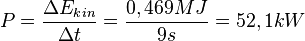P=\frac{\Delta E_{kin}}{\Delta t}=\frac{0,469MJ}{9s}=52,1kW, also deutlich mehr als dooppelt so groß als beim Beschleunigen bei hohen Geschwindigkeiten.

b) Der Zacken am Anfang entsteht durch den Schaltvorgang. Man tritt die Kupplung und schaltet. Während dieser Zeit wirkt keine Motorkraft, die Geschwindigkeit nimmt ab. Nach dem Schalten in den nächsten Gang wirkt wieder die Motorkraft und der Wagen beschleunigt weiter. Dies macht sich bei kleinen Geschwindigkeiten stärker bemerkbar als bei größeren Geschwindigkeiten.


Bleistift 35fach.jpg   Aufgabe 9

Buch S. 71 / 1,

Buch S. 71 / 2,

Buch S. 71 / 3

71/1 Ein Flugzeug fliegt mit konstanter Geschwindigkeit, daher ist 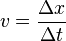v=\frac{\Delta x}{\Delta t}. Mit den angegebenen Werten berechnet man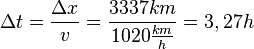 \Delta t=\frac{\Delta x}{v}=\frac{3337km}{1020\frac{km}{h}}=3,27h
Es ist gerade 15:02 Uhr

71/2 a) Es ist 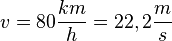v=80\frac{km}{h}=22,2\frac{m}{s}. Mit dieser konstanten Geschwindigkeit legt man in 5s die Strecke 111m zurück.
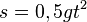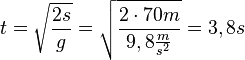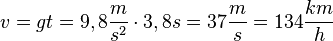Allerdings hat man bei dem Fahrgeschäft keine Bewegung mit konstanter Geschwindigkeit, sondern oben ist die Geschwindigkeit 0 und nach dem Losfahren hat man eine Bewegung mit konstanter Beschleunigung. Für die beschleunigte Bewegung ist s = 0,5g t^2. Nimmt man s = 70m, dann ist t=\sqrt {\frac{2s}{g}}=\sqrt {\frac{2\cdot 70m}{9,8\frac{m}{s^2}}}=3,8s. Dabei erreicht man die Geschwindigkeit v=gt=9,8\frac{m}{s^2}\cdot 3,8s=37\frac{m}{s}=134\frac{km}{h}.
Die Durchschnittsgeschwindigkeit ist 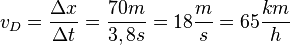v_D=\frac{\Delta x}{\Delta t}=\frac{70m}{3,8s}=18\frac{m}{s}=65\frac{km}{h}.
Beachte, dass du für eine beschleunigte Bewegung nicht s = vt verwenden darfst, sondern du musst 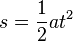s=\frac{1}{2}at^2 nehmen.


Die gegebenen Daten in der Aufgabe s = 70m, t = 5s und v = 80km/h passen nicht zusammen. Die Höhe s des Turms ist gegeben, da kann man nichts ändern, die Zeit t lässt sich leicht mit einer Uhr messen. Einen Geschwindigkeitsmesser hat man normal nicht dabei. Nimmt man eine Bewegung mit konstanter Geschwindigkeit an, dann ist die Geschwindigkeit 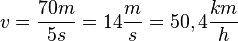v=\frac{70m}{5s}=14\frac{m}{s}=50,4\frac{km}{h}, also passt die Aussage 80km/h nicht.
Nimmt man eine beschleunigte Bewegung, dann hat man oben für die Fallzeit t = 3,8s berechnet. Gut, die Sitze müssen auch noch abgebremst werden, so dass man auf 5s kommen kann. Die Abbremsung erfolgt vielleicht auf den letzten 10m. Dann ist die Fallzeit 3,5s und die erreichte Höchstgeschwindigkeit 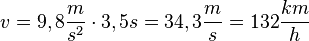v=9,8\frac{m}{s^2}\cdot 3,5s=34,3\frac{m}{s}=132\frac{km}{h}, passt also auch nicht.
Nimmt man für die Durchschnittsgeschwindigkeit 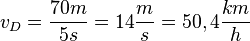v_D=\frac{70m}{5s}=14\frac{m}{s}=50,4\frac{km}{h}, passt also auch nicht.

71/3 a) Du fährst mit konstanter Geschwindigkeit 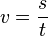v=\frac{s}{t}, dann ist 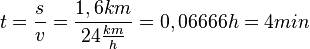t=\frac{s}{v}=\frac{1,6km}{24\frac{km}{h}}=0,06666h=4min. Du erreichst die Schule in 4 Minuten.

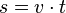
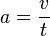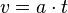b) Um schon in 3 Minuten an der Schule zu sein, musst du schneller fahren, also beschleunigen und dann mit größerer konstanter Geschwindigkeit weiterfahren. Dies kann z.b. passieren, wenn es bergab geht.
Von „http://rsg.zum.de/index.php?title=Ph9_tx-_und_tv-_Abhängigkeiten&oldid=11232“