M9 Quadratische Funktionen und Extremwerte: Unterschied zwischen den Versionen
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 26: | Zeile 26: | ||
Die y-Koordinate des Scheitels y<sub>S</sub> erhält man, indem man x<sub>S</sub> in die Parabelgleichung einsetzt.}} | Die y-Koordinate des Scheitels y<sub>S</sub> erhält man, indem man x<sub>S</sub> in die Parabelgleichung einsetzt.}} | ||
| − | {{Aufgaben-blau|1|2= | + | {{Aufgaben-blau|1|2=Von einer rechteckigen Glasplatte mit Länge l = 85cm und Breite b = 50cm ist oben rechts die Ecke abgebrochen. Die rechte Seite hat nur noch die Länge 40cm, die obere Seite die Länge 60cm. Aus der fünfeckigen Restplatte soll durch Schnitte parallel zu den Seiten des ursprünglichen Rechtecks eine größtmögliche neue rechteckige Platte herausgeschnitten werden. |
<center><ggb_applet height="250" width="350" | <center><ggb_applet height="250" width="350" | ||
| − | filename="92-3.ggb" /></center>}} | + | filename="92-3.ggb" /></center> |
| + | a) Welche Maße hat die neue Platte?<br> | ||
| + | b) Wie viel Prozent der usprünglichen Plattenfläche nimmt sie ein?}} | ||
Wenn man den Punkt auf der schrägen Strecke bewegt, sieht man wie sich das Rechteck ändert. Die Fläche des Rechtecks wird angezeigt und man stellt fest, dass der Flächeninhalt A des Rechtsecks am größten ist, wenn x = 85 ist und es ist A = 3400cm<sup>2</sup>. | Wenn man den Punkt auf der schrägen Strecke bewegt, sieht man wie sich das Rechteck ändert. Die Fläche des Rechtecks wird angezeigt und man stellt fest, dass der Flächeninhalt A des Rechtsecks am größten ist, wenn x = 85 ist und es ist A = 3400cm<sup>2</sup>. | ||
| − | {{Lösung versteckt|1=Der obere, rechte Eckpunkt bewegt sich auf einer Geraden mit der Gleichung <math>y=-\frac{2}{5}x+74</math>. | + | {{Lösung versteckt|1=a) Der obere, rechte Eckpunkt bewegt sich auf einer Geraden mit der Gleichung <math>y=-\frac{2}{5}x+74</math>. |
x kann nur Werte von 60 bis 85 annehmen, also <math>x \in [60;85]</math>. <br> | x kann nur Werte von 60 bis 85 annehmen, also <math>x \in [60;85]</math>. <br> | ||
Der Flächeninhalt A ist <math>A=x \cdot y = x \cdot (-\frac{2}{5}x+74)=-\frac{2}{5}x^2+74x</math>. Der Funktionsterm ist der Term einer Gleichung einer nach unten geöffneten Parabel. <br> | Der Flächeninhalt A ist <math>A=x \cdot y = x \cdot (-\frac{2}{5}x+74)=-\frac{2}{5}x^2+74x</math>. Der Funktionsterm ist der Term einer Gleichung einer nach unten geöffneten Parabel. <br> | ||
| − | Der Term lässt sich umformen in <math>-\frac{2}{5}x^2+74x=\frac{2}{5}x(-x+185)</math>. An diesem Term sieht man leicht seine Nullstellen. Es ist <math>\frac{2}{5}x(-x+185)=0</math> für <math>x_1=0</math> und <math>x_2=185</math>, also schneidet die Parabel die x-Achse in <math>x_1=0</math> und <math>x_2=185</math>. Ihr Scheitel liegt bei <math>x_S=\frac{1}{2}(x_1+x_2)=92,5</math>. Dieser x-Wert liegt nicht in der Definitionsmenge [60;85] für x. Da es sich um eine nach unten geöffnete Parabel handelt und die x-Werte von 60 bis 85 links vom Scheitel liegen, nehmen die Parabelwerte zum Scheitel hin zu und der größte Wert auf der Parabel ist bei x = 85 erreicht. | + | Der Term lässt sich umformen in <math>-\frac{2}{5}x^2+74x=\frac{2}{5}x(-x+185)</math>. An diesem Term sieht man leicht seine Nullstellen. Es ist <math>\frac{2}{5}x(-x+185)=0</math> für <math>x_1=0</math> und <math>x_2=185</math>, also schneidet die Parabel die x-Achse in <math>x_1=0</math> und <math>x_2=185</math>. Ihr Scheitel liegt bei <math>x_S=\frac{1}{2}(x_1+x_2)=92,5</math>. Dieser x-Wert liegt nicht in der Definitionsmenge [60;85] für x. Da es sich um eine nach unten geöffnete Parabel handelt und die x-Werte von 60 bis 85 links vom Scheitel liegen, nehmen die Parabelwerte zum Scheitel hin zu und der größte Wert auf der Parabel ist bei x = 85 erreicht. < |
| + | |||
| + | b) Die neue Platte hat den Flächeninhalt 3400cm², das sind <math>\frac{3400}{4250}=0,8=80%</math> der ursprünglichen Platte.}} | ||
| Zeile 56: | Zeile 60: | ||
{{Merksatz|MERK=Eine Parabel hat die Gleichung <math>y=ax^2+bx+c</math>. | {{Merksatz|MERK=Eine Parabel hat die Gleichung <math>y=ax^2+bx+c</math>. | ||
| − | Die Parabel ist nach oben geöffnet, wenn a > 0 ist, sie ist nach unten geöffnet wenn a | + | Die Parabel ist nach oben geöffnet, wenn a > 0 ist, sie ist nach unten geöffnet wenn a < 0 ist. |
Eine nach oben geöffnete Parabel (a > 0) hat ihren tiefsten Punkt im Scheitel. Dort ist y am kleinsten.<br> | Eine nach oben geöffnete Parabel (a > 0) hat ihren tiefsten Punkt im Scheitel. Dort ist y am kleinsten.<br> | ||
| Zeile 62: | Zeile 66: | ||
Hat eine Parabel zwei Nullstellen x<sub>1</sub> und x<sub>2</sub>, so ist die x-Koordinate x<sub>S</sub> des Scheitels der Mittelwert von x<sub>1</sub> und x<sub>2</sub>, also <math>x_S=\frac{x_1+x_2}{2}</math>. }} | Hat eine Parabel zwei Nullstellen x<sub>1</sub> und x<sub>2</sub>, so ist die x-Koordinate x<sub>S</sub> des Scheitels der Mittelwert von x<sub>1</sub> und x<sub>2</sub>, also <math>x_S=\frac{x_1+x_2}{2}</math>. }} | ||
| + | |||
| + | {{Aufgaben-blau|3|2= | ||
| + | [[Datei:Leitung.jpg|thumb|350px]] | ||
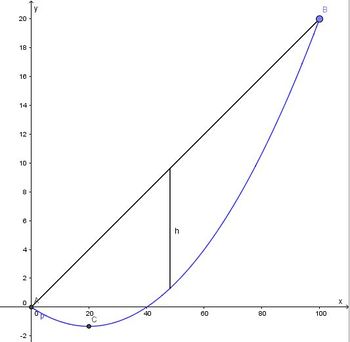
| + | Eine Hochspannungsleitung hängt zwischen den Punkten A und B näherungsweise parabelförmig durch. Aus dem Koordinatensystem liest man ab: A(0;0), B(100;20) und C(20;?). | ||
| + | |||
| + | a) Ermittle die Werte der Parameter a, d und e der Scheitelform y = a(x-d)² + e der Parabel. | ||
| + | Schreibe die Gleichung der Parabel in der Form y = ax² + bx + c bzw. y = a(x-x<sub>1</sub>)(x-x<sub>2</sub>). | ||
| + | |||
| + | b) Schreibe einen Term h(x) für den Durchhang h und finde heraus, an welcher Stelle der Durchhang am größen ist und bestimme den Wert h<sub>max</sub>. | ||
| + | }} | ||
| + | |||
| + | {{Lösung versteckt|1=Aus der Zeichnung und dem Text kann man die Koordinaten der Punkte angeben: A(0;0), B(100;20), C(20,e). Der Ursprung des Koordinatensystems liegt in A. Aus der Zeichnung sieht man auch noch die zweite Nullstelle D(40;0).<br> | ||
| + | a) Man hat die zwei Nullstellen, also ist <math>y=a\cdot x\cdot (x-40)</math>. <br> | ||
| + | Setzt man die Koordinaten von B in die Gleichung, dann ist <math> 20 = a \cdot 100(100-40)</math> und <math>a=\frac{1}{300}</math>. <br> | ||
| + | Die Gleichung der Parabel ist also <math>y=\frac{1}{300}x(x-40)</math> und wenn man den Term ausmultipliziert <math>y = \frac{1}{300}x^2 - \frac{2}{15}x</math>.<br> | ||
| + | Die Scheitelform ist <math>y = \frac{1}{300}(x-20)^2 -\frac{4}{3}</math>. | ||
| + | |||
| + | ----- | ||
| + | |||
| + | Oder wenn man mit der Scheitelform beginnt: <math>y=a(x-d)^2 + e</math> <br> | ||
| + | Vom Scheitel C(20;e) weiß man die x-Koordinate, also ist d = 20 und <math>y=a(x-20)^2+e</math>.<br> | ||
| + | Setzt man die Koordinaten von A in die Gleichung: (1) <math>0 = a\cdot (-20)^2 +e</math><br> | ||
| + | Setzt man die Koordinaten von B in die Gleichung: (2) <math>20 = a\cdot 80^2+e</math><br> | ||
| + | Subtrahiert man nun Gleichung (1) von Gleichung (2), so hat man <math>20 = 6400a - 400a</math> und <math>a=\frac{1}{300}</math>.<br> | ||
| + | Setzt man a in Gleichung (1), dann erhält man <math>0=\frac{1}{300}\cot 400 + e </math> und <math> e = -\frac{4}{3}</math>.<br> | ||
| + | Die Scheitelform ist <math>y = \frac{1}{300}(x-20)^2 -\frac{4}{3}</math>. <br> | ||
| + | Durch Ausmultiplizieren und zussammenfassen erhält man <math>y = \frac{1}{300}x^2 - \frac{2}{15}x</math>.<br> | ||
| + | In der letzten Gleichung kann man auf der rechten Seite <math>\frac{x}{300}</math> ausklammern und erhält <math>y=\frac{1}{300}x(x-40)</math>. | ||
| + | |||
| + | b) Der Durchhang h(x) ergibt sich als Differenz (bei gleichem x) der y-Koordinate der Geraden [AB] und der y-Koordinate der Parabel. <br> | ||
| + | Die Gerade [AB] hat die Gleichung <math>y = \frac{1}{5}x</math>.<br> | ||
| + | Die Gleichung der Parabel ist <math>y = \frac{1}{300}x^2 - \frac{2}{15}x</math>.<br> | ||
| + | Damit ist <math>h(x)= \frac{1}{5}x - (\frac{1}{300}x^2 - \frac{2}{15}x)</math>.<br> | ||
| + | Fasst man den Term auf der rechten Seite zusammen, dann erhält man <math>h(x)=-\frac{1}{300}x^2+\frac{1}{3}x</math>.<br> | ||
| + | Man will nun den größten Wert des Durchhangs wissen. Der Funktionsterm für h(x) ist eine nach unten geöffnete Parabel, die ihren größten y-Wert im Scheitel hat, also muss man den Scheitel bestimmen.<br> | ||
| + | Die x-Koordinate des Scheitels erhält man, wenn man die Mitte der zwei Nullstellen nimmt. Dafür klammert man auf der rechten Seite <math>-\frac{x}{300}</math> aus und erhält <math> h(x)=-\frac{1}{300}x(x-100)</math>. <br> | ||
| + | Hier kann die Nullstellen ablesen: <math>x_1=0, x_2=100</math> und genau in der Mitte ist die x-Koordinate des Scheitels <math>x_S=50</math>.<br> | ||
| + | Setzt man diesen Wert in h(x) ein, dann erhält man den größten Durchhang <math>h(50)=8\frac{1}{3}</math>. | ||
| + | }} | ||
| + | |||
| + | |||
| + | {{Aufgaben-blau|4|2=Bearbeite dieses [http://www.raschweb.de/M9-Extremwertaufgaben.pdf Arbeitsblatt]. }} | ||
Aktuelle Version vom 19. Februar 2022, 15:09 Uhr
Einem gleichseitigen Dreieck der Seitenlänge 6cm wird ein Rechteck so einbeschrieben, dass eine Rechteckseite l auf einer Dreieckseite liegt und die anderen Eckpunkte des Rechtecks auf den beiden anderen Dreieckseiten liegen. Im folgenden Applet ist die Situation dargestellt. Die Rechteckseite l liegt auf der Dreieckseite [AB].
Den Punkt E kann man auf der Dreieckseite [AB] bewegen. Dadurch ändert sich das Rechteck der Aufgabe. Über dem Wert der Rechteckseite l wird der Flächeninhalt  des Rechtecks aufgetragen. Dies ergibt im Applet den Punkt
des Rechtecks aufgetragen. Dies ergibt im Applet den Punkt  . Wenn man die Lage des Punktes E ändert, ändert sich auch die Rechteckfläche und der Punkt
. Wenn man die Lage des Punktes E ändert, ändert sich auch die Rechteckfläche und der Punkt  wandert. Der Punkt
wandert. Der Punkt 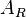 hat die Koordinaten
hat die Koordinaten 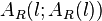
Das Rechteck hat Flächeninhalt 0, wenn l = 0 oder l = 6 ist. Gibt es ein Rechteck mit größtem Flächeninhalt?
Für den Punkt 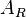 im Applet kann man die Spur anzeigen, die sich ergibt, wenn E bewegt wird. Man sieht, dass die Spur eine Parabel ergibt, deren Scheitel bei l = 3 liegt. Man kann auch den Wert von
im Applet kann man die Spur anzeigen, die sich ergibt, wenn E bewegt wird. Man sieht, dass die Spur eine Parabel ergibt, deren Scheitel bei l = 3 liegt. Man kann auch den Wert von 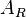 zu
zu 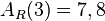 ablesen.
ablesen.
Da der Flächeninhalt 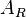 des einbeschriebenen Rechtecks von der Seitenlänge l abhängt, kann man eine Funktion
des einbeschriebenen Rechtecks von der Seitenlänge l abhängt, kann man eine Funktion 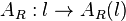 angeben, die für jeden Wert von
angeben, die für jeden Wert von ![l \in [0;6]](/images/math/f/e/8/fe8d7a0d06e68fce822e2fc4f5896284.png) den Wert
den Wert 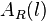 angibt. Für diese Funktion gilt es nun den Funktionsterm zu bestimmen.
angibt. Für diese Funktion gilt es nun den Funktionsterm zu bestimmen.
Der Punkt E kann vom Ursprung bis zum Mittelpunkt der Dreiecksseite [AB] gehen. Seine Koordinaten sind daher 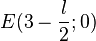 .
.
Die Dreiecksseite [AC] ist Teil einer Gerade, deren Geradengleichung y = mx + t wir bestimmen wollen. Da sie durch den Ursprung geht ist t = 0. Also müssen wir noch die Steigung m der Geraden bestimmen. Da das Dreieck ABC ein gleichseitiges Dreieck ist, wissen wir seit wir den Satz des Pythagoras kennen, dass die Höhe im gleichseitigen Dreieck mit der Seitenlänge a 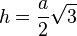 ist.
ist.
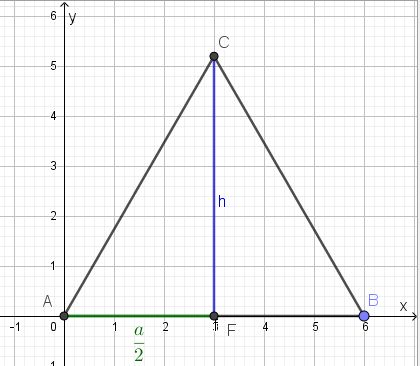
Die Steigung m ist dann 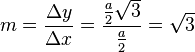
Die Gerade hat also die Gleichung 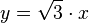 .
.
Damit können wir zur Länge l des Rechtecks nun die Breite b angeben. b geht von E senkrecht nach oben bis zur Dreiecksseite [AC]. b hat also den Wert 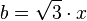 , wobei hier x die x-Koordinate des Punktes E ist, für die sich oben
, wobei hier x die x-Koordinate des Punktes E ist, für die sich oben 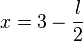 ergeben hat.
ergeben hat.
Die Rechtecksfläche ist dann 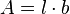 . Nun ist
. Nun ist 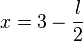 und damit
und damit 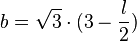 und damit
und damit 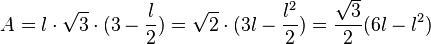 . Dies ist die Gleichung einer nach unten geöffneten Parabel, die ihre größten Wert im Scheitel annimmt.
. Dies ist die Gleichung einer nach unten geöffneten Parabel, die ihre größten Wert im Scheitel annimmt.
Die Nullstellen des Terms 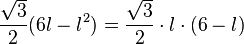 sind
sind 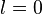 und
und 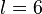 . Das hatten wir uns schon oben überlegt.
. Das hatten wir uns schon oben überlegt.
Der Scheitel der Parabel liegt genau in der Mitte zwischen den Nullstellen, also hier bei x = 3 und der Flächeninhalt des größten Rechtecks ergibt sich zu 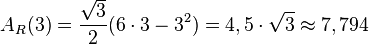 .
.
|
Merke:
Kennt man die Nullstellen x1 und x2 einer Parabel mit der Gleichung y = ax2 + bx + c, dann liegt ihr Scheitel genau in der Mitte zwischen den Nullstellen. |
Wenn man den Punkt auf der schrägen Strecke bewegt, sieht man wie sich das Rechteck ändert. Die Fläche des Rechtecks wird angezeigt und man stellt fest, dass der Flächeninhalt A des Rechtsecks am größten ist, wenn x = 85 ist und es ist A = 3400cm2.
a) Der obere, rechte Eckpunkt bewegt sich auf einer Geraden mit der Gleichung 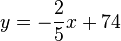 .
x kann nur Werte von 60 bis 85 annehmen, also
.
x kann nur Werte von 60 bis 85 annehmen, also ![x \in [60;85]](/images/math/b/2/8/b286be4ebb99bcd363e6d80f41d40cd1.png) .
.
Der Flächeninhalt A ist 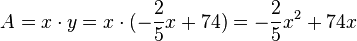 . Der Funktionsterm ist der Term einer Gleichung einer nach unten geöffneten Parabel.
. Der Funktionsterm ist der Term einer Gleichung einer nach unten geöffneten Parabel.
Der Term lässt sich umformen in 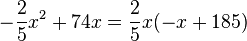 . An diesem Term sieht man leicht seine Nullstellen. Es ist
. An diesem Term sieht man leicht seine Nullstellen. Es ist 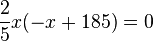 für
für 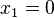 und
und 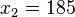 , also schneidet die Parabel die x-Achse in
, also schneidet die Parabel die x-Achse in 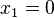 und
und 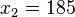 . Ihr Scheitel liegt bei
. Ihr Scheitel liegt bei 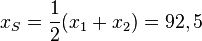 . Dieser x-Wert liegt nicht in der Definitionsmenge [60;85] für x. Da es sich um eine nach unten geöffnete Parabel handelt und die x-Werte von 60 bis 85 links vom Scheitel liegen, nehmen die Parabelwerte zum Scheitel hin zu und der größte Wert auf der Parabel ist bei x = 85 erreicht. <
. Dieser x-Wert liegt nicht in der Definitionsmenge [60;85] für x. Da es sich um eine nach unten geöffnete Parabel handelt und die x-Werte von 60 bis 85 links vom Scheitel liegen, nehmen die Parabelwerte zum Scheitel hin zu und der größte Wert auf der Parabel ist bei x = 85 erreicht. <
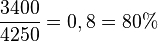 der ursprünglichen Platte.
der ursprünglichen Platte.
Es ist eine ähnliche Aufgabe zu Aufgabe 2, nur die Maße der Tischplatte und der abgebrochenen Ecke sind anders. Wenn man den Punkt P auf der schrägen Strecke bewegt, sieht man wie sich das Rechteck ändert. Die Fläche des Rechtecks wird angezeigt und man stellt fest, dass der Flächeninhalt A des Rechtecks, wenn P ganz oben ist A = 8100cm2 und wenn P ganz unten ist A=8400cm2 ist. Und dazwischen gibt es größere Werte als 8400cm2.
Der Punkt P sich auf einer Geraden mit der Gleichung 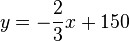 .
Die x-Koordinate von P kann nur Werte von 90 bis 120 annehmen, also
.
Die x-Koordinate von P kann nur Werte von 90 bis 120 annehmen, also ![x \in [60;85]](/images/math/b/2/8/b286be4ebb99bcd363e6d80f41d40cd1.png) .
.
Der Flächeninhalt A ist 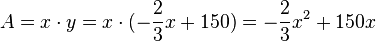 . Der Funktionsterm ist der Term einer Gleichung einer nach unten geöffneten Parabel.
. Der Funktionsterm ist der Term einer Gleichung einer nach unten geöffneten Parabel.
Der Term lässt sich umformen in 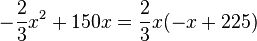 . An diesem Term sieht man leicht seine Nullstellen. Es ist
. An diesem Term sieht man leicht seine Nullstellen. Es ist 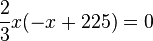 für
für 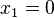 und
und 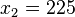 , also schneidet die Parabel die x-Achse in
, also schneidet die Parabel die x-Achse in 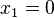 und
und 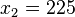 .
.
Die x-Koordinate des Scheitels 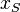 der Parabel liegt genau in der Mitte von 0 und 225, also
der Parabel liegt genau in der Mitte von 0 und 225, also 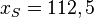 . Im Scheitel nimmt eine nach unten geöffnete Parabel ihren größen y-Wert an. Setzt man
. Im Scheitel nimmt eine nach unten geöffnete Parabel ihren größen y-Wert an. Setzt man 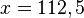 in die Gleichung
in die Gleichung 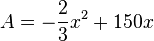 , dann erhält man
, dann erhält man 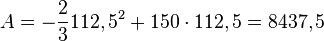 .
.
|
Merke:
Eine Parabel hat die Gleichung Die Parabel ist nach oben geöffnet, wenn a > 0 ist, sie ist nach unten geöffnet wenn a < 0 ist. Eine nach oben geöffnete Parabel (a > 0) hat ihren tiefsten Punkt im Scheitel. Dort ist y am kleinsten. Hat eine Parabel zwei Nullstellen x1 und x2, so ist die x-Koordinate xS des Scheitels der Mittelwert von x1 und x2, also |
Aus der Zeichnung und dem Text kann man die Koordinaten der Punkte angeben: A(0;0), B(100;20), C(20,e). Der Ursprung des Koordinatensystems liegt in A. Aus der Zeichnung sieht man auch noch die zweite Nullstelle D(40;0).
a) Man hat die zwei Nullstellen, also ist 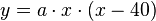 .
.
Setzt man die Koordinaten von B in die Gleichung, dann ist 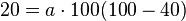 und
und 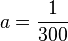 .
.
Die Gleichung der Parabel ist also 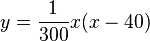 und wenn man den Term ausmultipliziert
und wenn man den Term ausmultipliziert 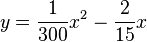 .
.
Die Scheitelform ist 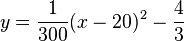 .
.
Oder wenn man mit der Scheitelform beginnt: 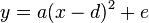
Vom Scheitel C(20;e) weiß man die x-Koordinate, also ist d = 20 und 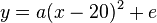 .
.
Setzt man die Koordinaten von A in die Gleichung: (1) 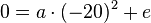
Setzt man die Koordinaten von B in die Gleichung: (2) 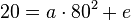
Subtrahiert man nun Gleichung (1) von Gleichung (2), so hat man 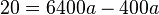 und
und 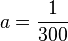 .
.
Setzt man a in Gleichung (1), dann erhält man 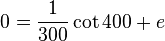 und
und 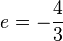 .
.
Die Scheitelform ist 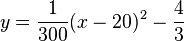 .
.
Durch Ausmultiplizieren und zussammenfassen erhält man 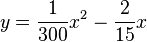 .
.
In der letzten Gleichung kann man auf der rechten Seite 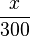 ausklammern und erhält
ausklammern und erhält 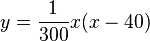 .
.
b) Der Durchhang h(x) ergibt sich als Differenz (bei gleichem x) der y-Koordinate der Geraden [AB] und der y-Koordinate der Parabel.
Die Gerade [AB] hat die Gleichung 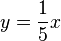 .
.
Die Gleichung der Parabel ist 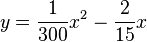 .
.
Damit ist 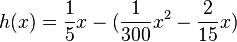 .
.
Fasst man den Term auf der rechten Seite zusammen, dann erhält man 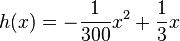 .
.
Man will nun den größten Wert des Durchhangs wissen. Der Funktionsterm für h(x) ist eine nach unten geöffnete Parabel, die ihren größten y-Wert im Scheitel hat, also muss man den Scheitel bestimmen.
Die x-Koordinate des Scheitels erhält man, wenn man die Mitte der zwei Nullstellen nimmt. Dafür klammert man auf der rechten Seite 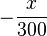 aus und erhält
aus und erhält 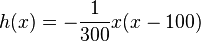 .
.
Hier kann die Nullstellen ablesen: 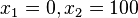 und genau in der Mitte ist die x-Koordinate des Scheitels
und genau in der Mitte ist die x-Koordinate des Scheitels 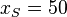 .
.
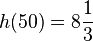 .
.

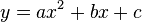 .
.
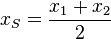 .
.