Lernpfad: Unterschied zwischen den Versionen
| Zeile 3: | Zeile 3: | ||
Du hast in der Einführung noch ein paar neue Begriffe kennengelernt, die du im folgenden Lernpfad gebrauchen kannst. Bearbeite nun den folgenden Lernpfad: <br> | Du hast in der Einführung noch ein paar neue Begriffe kennengelernt, die du im folgenden Lernpfad gebrauchen kannst. Bearbeite nun den folgenden Lernpfad: <br> | ||
<div style="margin:0; border:2px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#f1f1ff; align:left;"> | <div style="margin:0; border:2px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#f1f1ff; align:left;"> | ||
| − | |||
{{Aufgabe| | {{Aufgabe| | ||
| − | Bearbeite nun diesen | + | Bearbeite nun diesen [http://www.matheprisma.uni-wuppertal.de/Module/Hyperbel/index.htm Lernpfad] |
}} | }} | ||
</div> | </div> | ||
| Zeile 19: | Zeile 18: | ||
<div style="margin:0; border:2px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#f1f1ff; align:left;">'''Aufgabe''' | <div style="margin:0; border:2px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#f1f1ff; align:left;">'''Aufgabe''' | ||
| − | Stelle den Graphen der Funktion | + | Stelle den Graphen der Funktion nochmals [http://www.matheprisma.uni-wuppertal.de/Module/Hyperbel/SeiteZ1.htm auf dieser Seite] ein und gib an: <br> |
die vertikale Asymptote<br> | die vertikale Asymptote<br> | ||
die horizontale Asymptote<br> | die horizontale Asymptote<br> | ||
Aktuelle Version vom 11. August 2012, 16:50 Uhr
Station 1: Einführung - Station 2: Lernpfad - Station 3: Test
Du hast in der Einführung noch ein paar neue Begriffe kennengelernt, die du im folgenden Lernpfad gebrauchen kannst. Bearbeite nun den folgenden Lernpfad:
Hier hast du nun kennengelernt, dass auch andere Funktionen als die indirekte Proportionalität Hyperbeln als Graph haben.
Fasse das eben Gelernte zusammen und notiere es im Heft.
Stelle den Graphen der Funktion nochmals auf dieser Seite ein und gib an:
die vertikale Asymptote
die horizontale Asymptote
die Definitionslücke
Außerdem kennst du schon:
Desweiteren weißt du, wann ein Bruch den Wert 0 annimmt.
Der Funktionsterm der Funktion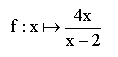 
ist ein Bruch. Welche x-Werte muss ich einsetzen, damit der Funktionswert 0 ist?
Weiter mit Station 3: Test
