M10 Aufgaben zum Logarithmus: Unterschied zwischen den Versionen
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 21: | Zeile 21: | ||
106/5 <br> | 106/5 <br> | ||
| − | a) man unterteilt eine Strecke von 5cm in Teile und beschriftet sie mit 1, 2, 3, ..., 10. Die Teile erhält man, indem man den untersten (1-ten Strich bei 0cm ) mit 1 beschriftet und den obersten Strich (bei 5cm) mit 10 beschriftet. Die anderen Beschriftungen für x = 1, 2, 3, ... 9 erhält man indem man lg(x) berechnet und diesen Wert im Abstand von unten mit der Beschriftung x anträgt. <br> | + | a) man unterteilt eine Strecke von 5cm in Teile und beschriftet sie mit 1, 2, 3, ..., 10. Die Teile erhält man, indem man den untersten (1-ten Strich bei 0cm ) mit 1 beschriftet und den obersten Strich (bei 5cm) mit 10 beschriftet. Die anderen Beschriftungen für x = 1, 2, 3, ... 9 erhält man indem man lg(x) berechnet, den Wert mit 5cm multipliziert und diesen Wert im Abstand von unten mit der Beschriftung x anträgt. <br> |
| + | Das macht man dann für die nächsten 5cm genauso, nur, dass man nun für x die Zahlen 20, 30, 40, ... 100 nimmt, dann lg(x) bildet, mit 5cm multipliziert und diese Länge von der untersten Linie (bei 0cm) aus anträgt. ...<br> | ||
b,c)<br> | b,c)<br> | ||
[[Datei:106-5.jpg]]<br> | [[Datei:106-5.jpg]]<br> | ||
| + | Man kann übrigens alle Zahlen auf der linken Seite, die man in der Aufgabe a) verwendet hat mit derselben Zehnerpotenzen multiplizieren. Die Skalierung bleibt. <br> | ||
d) Da sich der Hörbereich des Hundes mit dem Stimmbereich der Fledermaus überschneidet, hört der Hund Schreie einer Fledermaus. }} | d) Da sich der Hörbereich des Hundes mit dem Stimmbereich der Fledermaus überschneidet, hört der Hund Schreie einer Fledermaus. }} | ||
{{Aufgaben-blau|4|2=Buch S. 107 / 6 (Richter-Skala)<br> | {{Aufgaben-blau|4|2=Buch S. 107 / 6 (Richter-Skala)<br> | ||
Buch S. 108 / 7 (Lautstärke) }} | Buch S. 108 / 7 (Lautstärke) }} | ||
| + | |||
| + | {{Lösung versteckt|1=107/6<br> | ||
| + | a) Es ist <math>lg(\frac{a}{a_0})=lg(\frac{10000a_0}{a_0})=lg(10^4)=4</math>: von Menschen kaum bemerkbar, eventuell klappern schon Gläser und Teller <br> | ||
| + | <math>lg(\frac{a}{a_0}=lg(\frac{100000a_0}{a_0})=lg(10^5)=5</math>: Gläser und Teller klappern, eventuell gibt es schon Risse im Putz von Häusern<br> | ||
| + | <math>lg(\frac{a}{a_0}=lg(\frac{1000000a_0}{a_0})=lg(10^6)=6</math>: Risse im Putz von Häusern | ||
| + | |||
| + | b) <math>lg(\frac{a}{a_0)}=9,5</math> ergibt <math>a = 10^{9,5}a_0\approx 3,2\cdot 10^9</math>, die größte Auslenkung ist über 3 Milliarden mal größer als <math>a_0</math>.<br> | ||
| + | Bei einem Erdbeben der Stärke 5 ist die größte Auslenkung <math>a = 10^5\cdot a_0</math>, Also ist bei ein Beben der Stärke 9,5 die größte Auslenkung <math>\frac{3,2\cdot 10^9}{10^5}=3,2\cdot 10^4</math>, also etwa 3200 mal größer als die größte Auslenkung bei einem Beben der Stärke 5. | ||
| + | |||
| + | c) Dafür spricht: Erdbeben fallen ganz unterschiedlich aus und ihre Wirkungen reichen von "nicht wahrnehmbar" bis "gewaltigste Zerstörung". Dies wird durch Amplitude von registrierten Erschütterungen gemessen und die können ein zig-Tausendfaches der kleinsten Amplitude sein. Um daher ein vernüngtiges Verhältnis darstellen zu können ist es sinnvoll eine logarithmische Skala zu verwenden. <br> | ||
| + | Dagegen spricht: mit kleinen Zahlen (die Zahlen auf der Richter-Skala geben für Beben meist Zahlen < 10 an) werden gewaltige Wirkungen beschrieben und man unterschätzt aufgrund der kleinen Zahlen diese Wirkungen. | ||
| + | |||
| + | '''Tipp:''' Auf der Website vom [https://www.gfz-potsdam.de/medien-kommunikation/aktuelle-erdbebeninformationen/ Deutschen Geoforschungszentrum] findest du Informationen über Erdbeben und eine [http://geofon.gfz-potsdam.de/eqinfo/seismon/globmon.php aktuelle Karte] über (gerade) registrierte Erdbeben. | ||
| + | |||
| + | 108/7<br> | ||
| + | a)<br> | ||
| + | [[Datei:108-7a.jpg]]<br> | ||
| + | b) Wenn 10 Personen flüstern, addieren sich die Schallintensitäten, die Schallintensität von 10 flüsterneden Personen ist dann <math>10\cdot 10^{-10}\frac{W}{m^2}=10^{-9}\frac{W}{m^2}</math> und die Lautstärke <math>L = 10\cdot lg(\frac{10^{-9}}{10^{-12}} dB=10\cdot lg(10^3)dB = 30dB</math> | ||
| + | |||
| + | c) Wenn sich die Schallintensität I verdoppelt, dann ist I = 2I<sub>0</sub> und <math>L = 10\cdot lg(\frac{2I_0}{I_0})dB=10\cdot lg(2) dB = 3,01dB</math>, also hat sich die Lautstärke um 3 größer geworden.ändert. | ||
| + | |||
| + | d) <math>L = 10\cdot lg(\frac{I}{I_0})</math> ist nach <math>I</math> aufgelöst: <math>I = I_0\cdot 10^{\frac{L}{10}}=10^{-12}\cdot 10^{\frac{L}{10}}=10^{\frac{L}{10}-12}</math>.<br> | ||
| + | L = 1dB ergibt in die Gleichung <math>I = 10^{\frac{L}{10}-12}</math> eingesetzt: <math>I = 10^{\frac{1}{10}-12}= 1,26\cdot 10^{-12}=1,26I_0</math><br> | ||
| + | Die Schallintensität wird um 26% größer. | ||
| + | |||
| + | e) Für L = 95dB ist <math>I = 10^{\frac{95}{10}-12}= 0,00316 \approx 3.2\cdot 10^9 I_0</math>.<br> | ||
| + | Für L = 110dB ist <math>I = 10^{\frac{110}{10}-12}= 0,1 \approx 10^{11} I_0</math>. }} | ||
Aktuelle Version vom 16. April 2021, 06:22 Uhr
Bei einem Logarithmuspapier sind eine oder beide Achsen mit einer logarithmischen Skala versehen.
Mehr zum Logarithmuspapier findest du auf dieser Seite bei Wikipedia
Sachverhalte, die durch ein logarithmisches oder Exponentialgesetz gegeben sind lassen sich als Geraden darstellen. In einem Diagramm kann man Geraden leichter identifizieren als die vorgegebene Funktion.
106/5
a) man unterteilt eine Strecke von 5cm in Teile und beschriftet sie mit 1, 2, 3, ..., 10. Die Teile erhält man, indem man den untersten (1-ten Strich bei 0cm ) mit 1 beschriftet und den obersten Strich (bei 5cm) mit 10 beschriftet. Die anderen Beschriftungen für x = 1, 2, 3, ... 9 erhält man indem man lg(x) berechnet, den Wert mit 5cm multipliziert und diesen Wert im Abstand von unten mit der Beschriftung x anträgt.
Das macht man dann für die nächsten 5cm genauso, nur, dass man nun für x die Zahlen 20, 30, 40, ... 100 nimmt, dann lg(x) bildet, mit 5cm multipliziert und diese Länge von der untersten Linie (bei 0cm) aus anträgt. ...
b,c)
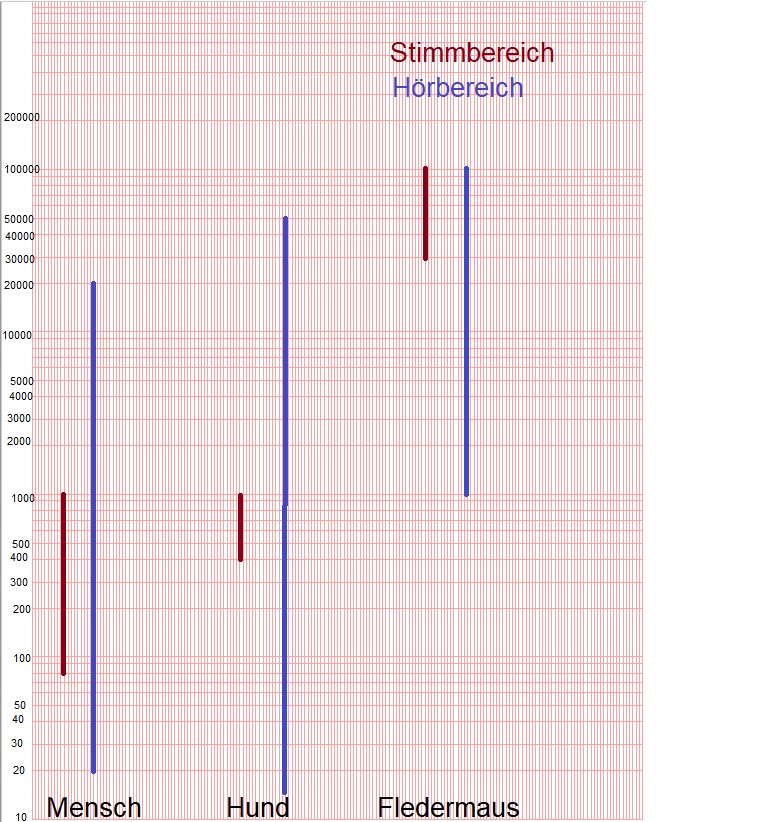
Man kann übrigens alle Zahlen auf der linken Seite, die man in der Aufgabe a) verwendet hat mit derselben Zehnerpotenzen multiplizieren. Die Skalierung bleibt.
107/6
a) Es ist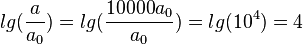 
: von Menschen kaum bemerkbar, eventuell klappern schon Gläser und Teller
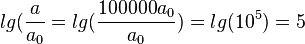: Gläser und Teller klappern, eventuell gibt es schon Risse im Putz von Häusern
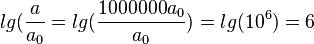: Risse im Putz von Häusern
b)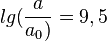 
ergibt 
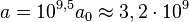, die größte Auslenkung ist über 3 Milliarden mal größer als 
.
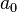Bei einem Erdbeben der Stärke 5 ist die größte Auslenkung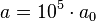 
, Also ist bei ein Beben der Stärke 9,5 die größte Auslenkung 
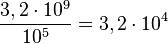, also etwa 3200 mal größer als die größte Auslenkung bei einem Beben der Stärke 5.
c) Dafür spricht: Erdbeben fallen ganz unterschiedlich aus und ihre Wirkungen reichen von "nicht wahrnehmbar" bis "gewaltigste Zerstörung". Dies wird durch Amplitude von registrierten Erschütterungen gemessen und die können ein zig-Tausendfaches der kleinsten Amplitude sein. Um daher ein vernüngtiges Verhältnis darstellen zu können ist es sinnvoll eine logarithmische Skala zu verwenden.
Dagegen spricht: mit kleinen Zahlen (die Zahlen auf der Richter-Skala geben für Beben meist Zahlen < 10 an) werden gewaltige Wirkungen beschrieben und man unterschätzt aufgrund der kleinen Zahlen diese Wirkungen.
Tipp: Auf der Website vom Deutschen Geoforschungszentrum findest du Informationen über Erdbeben und eine aktuelle Karte über (gerade) registrierte Erdbeben.
108/7
a)
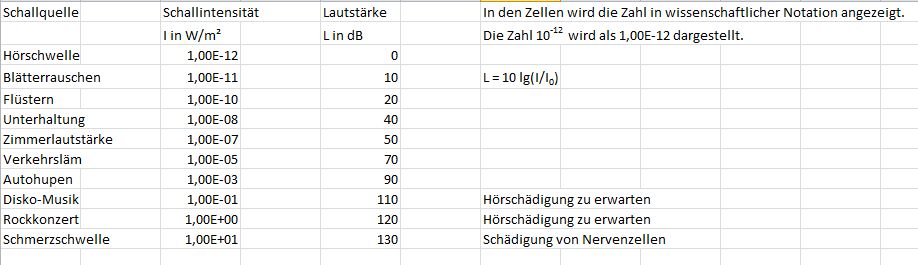
b) Wenn 10 Personen flüstern, addieren sich die Schallintensitäten, die Schallintensität von 10 flüsterneden Personen ist dann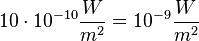 
und die Lautstärke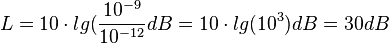 
c) Wenn sich die Schallintensität I verdoppelt, dann ist I = 2I0 und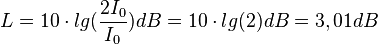 
, also hat sich die Lautstärke um 3 größer geworden.ändert.
d)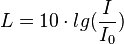 
ist nach 
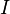aufgelöst: 
.
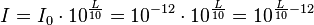L = 1dB ergibt in die Gleichung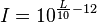 
eingesetzt: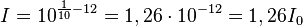 
Die Schallintensität wird um 26% größer.
e) Für L = 95dB ist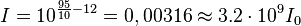 
.
.
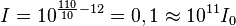