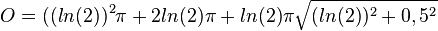M11 Aufgaben zu Logarithmus- und Exponentialfunktionen: Unterschied zwischen den Versionen
| (6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | __NOCACHE__ | ||
Buch S. 151 / 4 | Buch S. 151 / 4 | ||
| Zeile 48: | Zeile 49: | ||
b) Die Tangente in A soll parallel zu einer Geraden h mit Steigung - 0,5 sein. Also ist f'(x<sub>A</sub>) = - 0,5.<br> | b) Die Tangente in A soll parallel zu einer Geraden h mit Steigung - 0,5 sein. Also ist f'(x<sub>A</sub>) = - 0,5.<br> | ||
| − | <math>- 0,5 = -\frac{1}{2}e^{-\frac{x}{2}} \qquad | \cdot (-2)</math> | + | <math>- 0,5 = -\frac{1}{2}e^{-\frac{x}{2}} \qquad | \cdot (-2)</math><br> |
<math>1 =e^{-\frac{x}{2}} \qquad |logarithmieren</math><br> | <math>1 =e^{-\frac{x}{2}} \qquad |logarithmieren</math><br> | ||
<math>ln(1) = -\frac{x}{2}</math> ergibt <math>0 = -\frac{x}{2}</math> und <math> x = 0</math>. <br> | <math>ln(1) = -\frac{x}{2}</math> ergibt <math>0 = -\frac{x}{2}</math> und <math> x = 0</math>. <br> | ||
A(0;1) [[Datei:152-8b 1.jpg|350px]] | A(0;1) [[Datei:152-8b 1.jpg|350px]] | ||
| − | Die Tangente in B soll senkrecht zu einer Geraden k mit Steigung -2 sein. Die Tangente in B an G<sub>g</sub> hat dann die Steigung 0,5. Also ist g'(x<sub>B</sub>) = 0,5.<br< | + | Die Tangente in B soll senkrecht zu einer Geraden k mit Steigung -2 sein. Die Tangente in B an G<sub>g</sub> hat dann die Steigung 0,5. Also ist g'(x<sub>B</sub>) = 0,5.<br> |
| − | <math>0,5=\frac{1}{2}e^{x+1} \qquad |\cdot 2</math< | + | Zwei Geraden g<sub>1</sub>: y = m<sub>1</sub>x+t<sub>1</sub> und g<sub>2</sub>: y = m<sub>2</sub>x + t<sub>2</sub> stehen senkrecht zueinander, wenn m<sub>1</sub>· m<sub>2</sub> = -1 ist. |
| − | <math>1=e^{x+1} \qquad |logarithmieren</math> | + | <math>0,5=\frac{1}{2}e^{x+1} \qquad |\cdot 2</math><br> |
| + | <math>1=e^{x+1} \qquad |logarithmieren</math><br> | ||
<math> 0 = x+1</math> ergibt <math> x = -1</math> <br> | <math> 0 = x+1</math> ergibt <math> x = -1</math> <br> | ||
| − | B(-1;0,5) [[Datei:152-8b 2.jpg | + | B(-1;0,5) [[Datei:152-8b 2.jpg]] |
| + | }} | ||
| − | Buch S. 153 / | + | Buch S. 153 / 14 |
| − | {{Lösung versteckt|1=Graph 1 gehört zu Funktion f (f ist die einzige Funktion mit D = R<sup>+</sup>.)<br> | + | {{Lösung versteckt|1=Graph 1 gehört zu Funktion f (f ist die einzige Funktion mit D = R<sup>+</sup>. Außerdem kann man den Funktionsterm vereinfachen. Es ist f(x) = 2xe<sup>ln(x)</sup>=2x<sup>2</sup> und der Graph ist eine halbe Parabel.)<br> |
| − | Graph 2 gehört zu Funktion d (d hat bei x = 0 eine Polstelle.)<br> | + | Graph 2 gehört zu Funktion d (d hat bei x = 0 eine Polstelle. )<br> |
| − | Graph 3 gehört zu Funktion a (e<sup>x</sup> wird um den Faktor 2 in y-Richtung gestreckt, ebenso in x-Richtung, also ist der Verlauf wie bei "e-Funktion" durch (0;2).)<br> | + | Graph 3 gehört zu Funktion a (e<sup>x</sup> wird um den Faktor 2 in y-Richtung gestreckt, ebenso in x-Richtung, also ist der Verlauf fast wie bei der "e-Funktion" durch (0;2).)<br> |
Graph 4 gehört zu Funktion b (-e<sup>x</sup> ist e<sup>x</sup> an der x-Achse gespiegelt und wird um 3 nach oben verschoben.)<br> | Graph 4 gehört zu Funktion b (-e<sup>x</sup> ist e<sup>x</sup> an der x-Achse gespiegelt und wird um 3 nach oben verschoben.)<br> | ||
Graph 5 gehört zu Funktion c (c ist die einzig verbleibende Funktion mit c(0) = 2.)<br> | Graph 5 gehört zu Funktion c (c ist die einzig verbleibende Funktion mit c(0) = 2.)<br> | ||
Graph 6 gehört zu Funktion e (e hat als einzige Funktion eine Nullstelle bei x = 1.) }} | Graph 6 gehört zu Funktion e (e hat als einzige Funktion eine Nullstelle bei x = 1.) }} | ||
| + | |||
| + | Buch S. 152 / 9 | ||
| + | |||
| + | {{Lösung versteckt|1=Zuerst zeichnet man den Sachverhalt.<br> | ||
| + | [[Datei:152-9.jpg]]<br> | ||
| + | Es ist f'(0) = 1, also ist die Steigung m = 1 der Tangente in (P0;1). Die Tangente hat dann die Gleichung y = x + 1. Sie schneidet die x-Achse in A(-1;0). <br> | ||
| + | Die Normale zur Tangente in P hat dann die Steigung m = -1 und sie hat die Gleichung y = -x +1. Sie schneidet die x-Achse in B(1;0).<br> | ||
| + | Das Dreieck ABP ist ein gleichschenkliges, rechtwinkliges Dreieck. Der Winkel bei P ist 90<sup>o</sup>, die Basiswinkel sind jeweils 45<sup>o</sup>. }} | ||
| + | |||
| + | Buch S. 152 / 12<br> | ||
| + | <center><ggb_applet height="400" width="600" | ||
| + | filename="152-12.ggb" /></center> | ||
| + | |||
| + | {{Lösung versteckt|1=a) Die Koordinaten des Schnittpunkts B liest man gleich aus dem Diagramm ab, da beide Graphen sich bei x = 0 schneiden. Es ist B(0;1).<br> | ||
| + | Die x-Koordinate von A erhält man durch Lösen der Gleichung <math>e^{0,5x} = 4-3e^{-0,5x} </math>.<br> | ||
| + | <math>e^{0,5x} = 4-3e^{-0,5x} \qquad |\cdot e^{0,5x}</math><br> | ||
| + | <math>e^{x} = 4e^{0,5x}-3 \qquad |-4e^{0,5x}+3</math><br> | ||
| + | <math>e^{x} - 4e^{0,5x}+3 = 0 </math><br> | ||
| + | Substituiert man <math>w = e^{0,5x}</math>, dann man hat die quadratische Gleilchung <math>w^2 - 4w + 3 = 0 </math> zu lösen. Es ist <math>w^2 - 4w + 3 = (w-1)(w-3) </math> und daher hat die Gleichung <math>w^2 - 4w + 3 = 0 </math> die zwei Lösungen <math>w_1=1, w_2 = 3</math>. Die Lösung <math>w_1=1</math> führt beim Resubstituieren auf <math>0,5x = ln(1)</math>, also <math> x = 0</math>. (Lösung für B!)<br> | ||
| + | Die zweite Lösung <math>w_2 = 3</math> führt beim Resubstituieren auf <math>0,5x = ln(3)</math> und <math> x = 2\cdot ln(3) = ln(9) \approx 2,19722</math>. Also ist A(ln9; 3). | ||
| + | |||
| + | b) Es ist S(a; e<sup>0,5a</sup>) und T(a;4-3e<sup>-0,5a</sup>) und die Länge der Strecke [ST] ist <math>\overline {ST} = 4-3e^{-0,5a} - e^{0,5a}</math> (T liegt über S, also ist bei y<sub>T</sub> - y<sub>S</sub> die Differenz positiv).<br> | ||
| + | Betrachtet man nun die Funktion <math>s:a\rightarrow 4 - 3e^{-0,5a} - e^{0,5a}</math> für <math>a \in [0;ln(9)]</math>, dann muss man das Maximum von s finden. Dazu setzt man die <math>s'(a)</math> gleich 0 und erhält bei VZW +/- das gesuchte a.<br> | ||
| + | <math>s'(a)= -3e^{-0,5a}\cdot(-0,5) - e^{0,5a}\cdot 0,5 = 1,5e^{-0,5a} - 0,5e^{0,5a}</math><br> | ||
| + | <math>1,5e^{-0,5a} - 0,5e^{0,5a}= 0 \qquad |+0,5e^{0,5a}</math> | ||
| + | <math>1,5e^{-0,5a} = 0,5e^{0,5a} \qquad |\cdot 2</math><br> | ||
| + | <math>3e^{-0,5a} = e^{0,5a} \qquad |\cdot e^{0,5a}</math><br> | ||
| + | <math>3 = e^a \qquad |logarithmieren</math> <br> | ||
| + | <math>a = ln(3) \approx 1,1</math><br> | ||
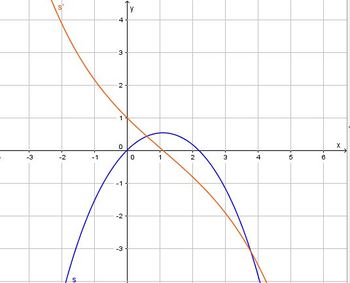
| + | Lässt man sich mit GeoGebra die Graphen von s und s' zeichnen, dann hat man dieses Bild:<br> | ||
| + | [[Datei:152-12b.jpg|350px]]<br> | ||
| + | und man sieht, dass s' bei a = ln(3) eine VZW +/- hat, also hat s bei a = ln(3) ein Maximum. }} | ||
| + | |||
| + | Buch S. 154 / 18 | ||
| + | |||
| + | {{Lösung versteckt|1=<math>f: x \rightarrow 9x\cdot e^{-x}</math> mit D = R.<br> | ||
| + | a) f(0) = 9\cdot 0 \cdot e<sup>0</sup> = 0, also ist (0;0) ein Punkt von G<sub>f</sub>.<br> | ||
| + | b) Es ist <math>9x\cdot e^{-x}=9\cdot \frac{x}{e^x}</math> und nach dem Grenzwert in der [http://www.isb.bayern.de/download/13107/merkhilfe_fuer_das_fach_mathematik_standard.pdf Merkhilfe] für r = 1 ist <math>\lim_{x\to \infty}f(x)=\lim_{x\to \infty}9x\cdot e^{-x}=\lim_{x\to\infty} 9\cdot \frac{x}{e^x}=0</math> | ||
| + | |||
| + | Für den Grenzwert <math>x \to -\infty</math> ist <math>\lim_{x\to -\infty}f(x) =\ </math>" <math>9\cdot(-\infty) \cdot \infty</math> "<math>= -\infty</math> | ||
| + | |||
| + | c) Es ist <math>f'(x)=9e^{-x}+9x\cdot e^{-x}\cdot(-1)=9e^{-x}(1-x)</math><br> | ||
| + | Da stets <math>e^{-x} > 0</math> ist, ist <math>f'(x)=0</math> für 1 - x = 0 und x = 1. <br> | ||
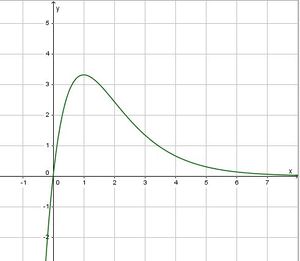
| + | Da y = 1 - x eine fallende Gerade mit Nullstelle x = 1 ist, ist dort der VZW +/- und damit ist bei x = 0 ein Maximum, G<sub>f</sub> hat in (1;<math>\frac{9}{e}</math>) einen Hochpunkt. | ||
| + | |||
| + | d)<br> | ||
| + | [[Datei:154-18.jpg|300px]] | ||
| + | |||
| + | e) Das Bild zu dieser Aufgabe schaut so aus:<br> | ||
| + | [[Datei:154-18e.jpg|300px]]<br> | ||
| + | Aufstellen der Gleichung der Tangente:<br> | ||
| + | <math>f(2) = 18\cdot e^{-2} = \frac{18}{e^2}\approx 2,436</math>. <br> | ||
| + | <math>f'(2)=9e^{-2}(1-2)=\frac{-9}{e^2}\approx 1,218</math>. <br> | ||
| + | Ansatz: <math> y = mx + t</math> mit <math>m = \frac{-9}{e^2}</math> und <math>P(2;\frac{18}{e^2}</math> erhält man<br> | ||
| + | <math> \frac{18}{e^2} = \frac{-9}{e^2}\cdot 2 + t </math><br> | ||
| + | <math> t = \frac{36}{e^2} \approx 4,872</math><br> | ||
| + | Die Gleichung der Tangente t ist <math> y=\frac{-9}{e^2}x + \frac{36}{e^2}</math>. | ||
| + | |||
| + | Der Schnittpunkt mit der y-Achse ist <math>(0;\frac{36}{e^2}</math>), der Schnittpunkt mit der x-Achse ist (4;0) | ||
| + | |||
| + | Der Flächeninhalt <math>a_1</math> des Dreiecks TIP ist <math>A_1=\frac{1}{2}\cdot 2 \cdot (\frac{36}{e^2} - \frac{18}{e^2})\approx 2,436</math><br> | ||
| + | Der Flächeninhalt <math>A</math> des Dreiecks OST ist <math>A=\frac{1}{2}\cdot 4\cdot \frac{36}{e^2}\approx 9,744</math><br> | ||
| + | Das Flächenverhältnis ist <math>\frac{A_1}{A}=\frac{1}{4}</math>, also nimmt die Fläche des Dreicks TIP 25% der Fläche des Dreiecks OST ein.<br> | ||
| + | Diese Aufgabe hätte man auch leichter mit dem Strahlensatz lösen können. Die "kleine waagrechte Strecke" [IP] hat die Länge 2, die "große waagrechte Strecke" [OS] hat die Länge 4. Daher ist der Faktor 2 und für das Verhältnis "Fläche kleines Dreieck" : "Fläche großes Dreieck" = 1 : 2<sup>2</sup> = 1 : 4. Damit hat man das gleiche Ergebnis. | ||
| + | |||
| + | f) Die Situation schaut so aus:<br> | ||
| + | [[Datei:154-18f.jpg|300px]]<br> | ||
| + | Der Flächeninhalt des Dreiecks OLA ist <math>A(s) = \frac{1}{2}\cdot s \cdot f(s) = \frac{1}{2}\cdot s \cdot 9se^{-s}=\frac{9}{2}\cdot s^2\cdot e^{-s}</math><br> | ||
| + | <math>A'(s) = \frac{9}{2}[2se^{-s}+s^2e^{-s}(-1)]=\frac{9}{2}e^{-s}s(2-s)</math> <br> | ||
| + | Es ist <math>\frac{9}{2}e^{-s} > 0</math> und <math>s (2-s)=2s-s^2</math> ist der Term einer nach unten geöffneten Parabel mit den Nullstellen 0 und 2. Da die Parabel nach unten geöffnet ist, ist bei s = 0 ein VZW -/+ und bei s = 2 ein VZW +/-. Daher hat A bei x = 2 ein Maximum und es ist <math>A(2) = 18e^{-2}=\frac{18}{e^2}\approx 2,436</math>. }} | ||
| + | |||
| + | Buch S. 159 / 6 | ||
| + | |||
| + | {{Lösung versteckt|1=<math>f(x) = (1-ln(x))^2</math> D = R<sup>+</sup><br> | ||
| + | Gemeinsame Punkte mit der x-Achse: <math>(1-ln(x))^2=0</math> ist erfüllt für <math>1=ln(x)</math>, also <math>x=e</math>.<br> | ||
| + | <math>f'(x)=2(1-ln(x))\cdot (-\frac{1}{x})=\frac{2(ln(x)-1)}{x}</math><br> | ||
| + | Für x<math>\in</math>R<sup>+</sup> ist der Nenner positiv. Für das Vorzeichen von f' muss man also den Zähler betrachten. <br> | ||
| + | Für x < e ist ln(x) < 1 und ln(x) - 1 < 0, also ist f'(x) < 0 für x < e und f ist in ]0;e] streng monoton abnehmend. <br> | ||
| + | Für x > e ist ln(x) > 1 und ln(x) - 1 > 0, also ist f'(x) > 0 für x > e und f ist in ]e;<math>\infty</math>[ streng monoton zunehmend. <br> | ||
| + | Da x = e die einzige Nullstelle von f' ist und einen VZW -/+ hat ist bei (e;0) ein Minimum und G<sub>f</sub> hat in (e;0) einen Tiefpunkt. <br> | ||
| + | Die positive y-Achse ist Asymptote für <math>x \to 0</math>. }} | ||
| + | |||
| + | Buch S. 160 / 10 | ||
| + | |||
| + | {{Lösung versteckt|1=<math>f(x) = ln(x^2+\frac{1}{4}) - ln(x)</math>, D = R<sup>+</sup><br> | ||
| + | a) Es ist <math>ln(x^2+\frac{1}{4}) - ln(x)=ln \left ( \frac{x^2 + 0,25}{x} \right )</math><br> | ||
| + | Gemeinsame Punkte mit der x-Achse erhält man, wenn <math>f(x) = 0 </math> ist. Es ist <math>ln \left (\frac{x^2+0,25}{x} \right )=0</math> für <math>\frac{x^2+0,25}{x} = 1</math>.<br> | ||
| + | <math>x^2+0,25 = x</math> ist eine quadratische Gleichung.<br> | ||
| + | <math>x^2 - x + 0,25 = 0</math> ergibt mit der binomischen Formel <math>(x-0,5)^2 = 0</math>, also ist x = 0,5 (doppelte) Nullstelle von f. | ||
| + | |||
| + | <math>f'(x) = \frac{1}{x^2+0,25} \cdot 2x - \frac{1}{x}=\frac{2x}{x^2+0,25}-\frac{1}{x}=\frac{2x^2 -(x^2+0,25)}{x(x^2+0,25)}=\frac{x^2-0,25}{x(x^2+0,25)}</math><br> | ||
| + | <math>f'(x) = 0</math> ist <math>\frac{x^2-0,25}{x(x^2+0,25)}=0</math>. Da der Nenner für positive x stets positiv ist, muss man nur den Zähler betrachten. Es ist <math>x^2-0,25=(x+0,5)(x-0,5)</math>. Der Zähler ist 0 für x = - 0,5 und x = 0,5. -0,5 ist nicht in D, also ist <math>f'(x)=0</math> für x = 0,5. <br> | ||
| + | Es ist <math>f(0,5)=ln(\frac{0,5^2+0,25}{0,5})=ln(1)=0</math><br> | ||
| + | Der Zähler ist eine nach oben geöffnete Parabel, die bei der rechten Nullstelle einen VZW -/+ hat. (Der Nenner ist positiv!). Daher hat f' bei x = 0,5 einen VZW -/+ und f hat bei x = 0,5 ein Minimum, G<sub>f</sub> bei (0,5;0) einen Tiefpunkt. | ||
| + | |||
| + | b) <math>\lim_{x\to 0+}[ln(x^2+\frac{1}{4}) - ln(x)]=\infty</math>, da ln(0,25) < 0 und <math>lim_{x\to 0}ln(x)=-\infty</math> ist.<br> | ||
| + | Die positive y-Achse ist für <math>x \to 0+</math> Asymptote. | ||
| + | |||
| + | <math>\lim_{x\to \infty}[ln(x^2+\frac{1}{4}) - ln(x)] =\lim_{x\to \infty}ln(\frac{x^2+0,25}{x}=\infty</math>, da der Grad des Zählerpolynoms 2 ist und damit größer als der Grad des Nennerpolynoms. Der Bruch geht für <math>x\to \infty</math> auch gegen <math>\infty</math>.<br> | ||
| + | Der Graph hat für <math>x\to \infty</math> keine Asymptote. | ||
| + | |||
| + | <math>\lim_{x\to \infty}[ln(x^2+\frac{1}{4}) - ln(x) -ln(x)]=\lim_{x\to \infty}[ln(x^2+0,25)-2ln(x)=\lim_{x\to \infty}\frac{x^2+0,25}{x^2}=ln(1)=0</math>, da der Grad des Zählerpolynoms gleich dem Grad des Nennerpolynoms ist. Damit geht der Bruch für <math>x\to \infty</math> gegen 1 .<br> | ||
| + | Die positive x-Achse ist für <math>x\to \infty</math> Asymptote. | ||
| + | |||
| + | c) <br> | ||
| + | [[Datei:160-10c.jpg|300px]] | ||
| + | |||
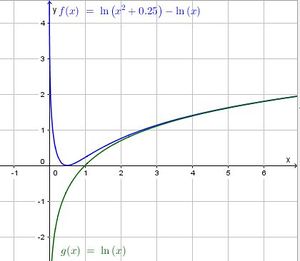
| + | d) g(x) = ln(x). Wenn im Argument 2x steht, dann wird der Graph von g um den Faktor 2 in x-Richtung gestaucht. <br> | ||
| + | [[Datei:160-10d.jpg|300px]]<br> | ||
| + | Den Schnittpunkt von G<sub>h</sub> und G<sub>f</sub> erhält man, wenn man <math>ln(2x) = ln(\frac{x^2+0,25}{x})</math> löst. Wenn die beiden Logarithmen gleich sind, müssen auch ihre Argumente gleich sein und man muss die Gleichung <math>2x = \frac{x^2+0,25}{x}</math> lösen.<br> | ||
| + | <math>2x = \frac{x^2+0,25}{x} \qquad |\cdot x</math> <br> | ||
| + | <math>2x^2 = x^2 + 0,25 \qquad |-x^2</math><br> | ||
| + | <math>x^2 = 0,25</math><br> | ||
| + | <math>x_{1,2}=\pm 0,5</math><br> | ||
| + | Da D = R<sup>+</sup> ist, hat man nur die Lösung x = 0,5 und der Schnittpunkt ist (0,5;0) (x = 0,5 ist Nullstelle, was man in a) gezeigt hat!)<br> | ||
| + | Den Schnittwinkel <math>\varphi</math> erhält man, wenn man <math>tan(\varphi_1)=h'(0,5)</math> und <math>tan(\varphi_2)=f'(0,5)</math> bestimmt und dann <math>\varphi = \varphi_1 - \varphi_2</math> berechnet.<br> | ||
| + | Es ist <math>h'(x)=\frac{1}{x}</math> , <math>tan(\varphi_1)=h'(0,5)=2</math> und <math>\varphi_1=63,4^o</math>.<br> | ||
| + | <math>tan(\varphi_2)=f'(0,5)=0</math> und <math>\varphi_2=0^o</math>. <br> | ||
| + | Also erhält man <math>\varphi = 63,4^o</math>. | ||
| + | |||
| + | e)<br> [[Datei:160-10e.jpg]]<br> | ||
| + | Wenn das Trapez um die x-Ache rotiert entsteht ein Zylinder, bei dem rechts ein Kegel herausgeschnitten ist. Die Grundfläche des Zylinders ist ein Kreis mit Mittelpunkt (0;0) und Radius r = ln(2). Die Höhe des Zylinders ist h = 1, also hat der Zylinder das Volumen <math>V_Z = r^2\pi \cdot h = (ln(2))^2 \pi</math>.<br> | ||
| + | Der Kegel, der recht herausgenommen wird hat ebenfalls den Radius r = ln(2), aber die Höhe h<sub>K</sub> = 0,5. Sein Volumen ist <math>V_K=\frac{1}{3}(ln(2))^2\cdot 0,5 \cdot \pi=\frac{(ln(2))^2}{6}\cdot \pi</math>.<br> | ||
| + | Damit hat der Rotationskörper das Volumen <math>V = V_Z - V_K = (ln(2))^2 \cdot \pi- \frac{(ln(2))^2}{6}\cdot \pi=\frac{5(ln(2))^2}{6}\cdot \pi</math>. | ||
| + | |||
| + | Die Oberfläche des Rotationskörpers setzt sich aus der Grundfläche des Zylinders, seiner Mantelfläche und der Mantelfläche des Kegel zusammen. Es ist <math>G = ((ln(2))^2\pi</math>, <math>M_Z=2r_Z\pi h_Z=2ln(2)\pi</math> und <math>M_K=r_K \pi m=ln(2)\pi\sqrt{(ln(2))^2 + 0,5^2}</math>.<br> | ||
| + | Damit ist <math>O = ((ln(2))^2\pi + 2ln(2)\pi + ln(2)\pi\sqrt{(ln(2))^2 + 0,5^2}</math> | ||
| + | |||
| + | |||
| + | |||
| + | }} | ||
Aktuelle Version vom 20. April 2021, 15:29 Uhr
Buch S. 151 / 4
151 / 4 Da man nur eine Stammfunktion angeben soll, wird auf + C verzichtet.
a) F(x) = ex + x
b) F(x) = - e-x
c) F(x) = 0,5(ex - e-x)
d) F(x) = 0,5x2 + 2x + ex+2
e) F(x) = e1+x
f) F(x) = 2e0,5x
Buch S. 152 / 7a
Es ist P(0;1), Q(2;e2), f'(x) = ex imd f'(0) = 1 und f'(2) = e2.
Gleichung der Tangente t1 in P: y = x + 1
Gleichung der Tangente t2 in Q: y = e2·x - e2. (t erhält man aus der Gleichung e2 = e2·2 - t.)
Den Schnittwinkel der beiden Tangenten erhält man, indem man 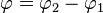 bildet, wenn
bildet, wenn 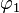 der Schnittwinkel von t1 mit der Waagrechten im Schnittpunkt und
der Schnittwinkel von t1 mit der Waagrechten im Schnittpunkt und 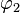 der Schnittwinkel von t2 mit der Waagrechten im Schnittpunkt ist.
der Schnittwinkel von t2 mit der Waagrechten im Schnittpunkt ist.
Es ist 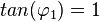 , also ist
, also ist 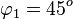 .
.
Es ist 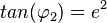 , also ist
, also ist 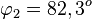
Damit ist 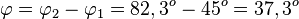 .
.
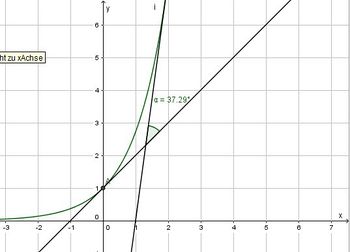
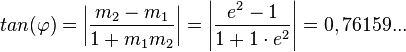 ergibt
ergibt 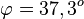 .
.Buch S. 152 / 8
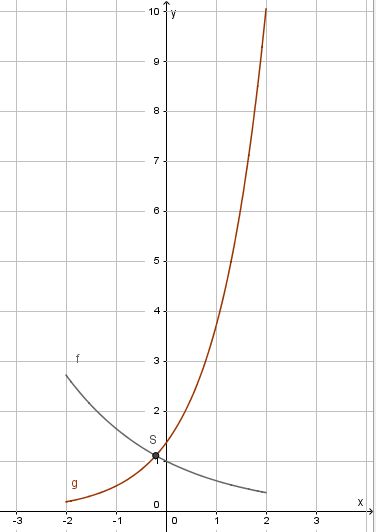
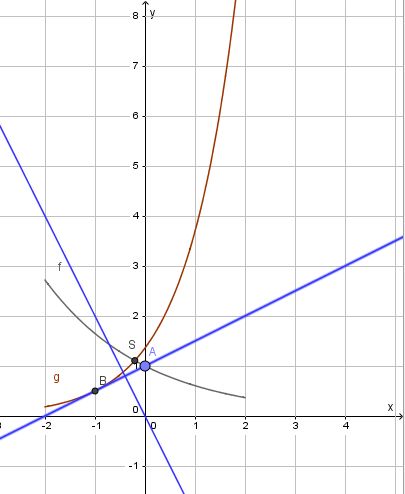
a) Die Koordinaten des Schnittpunkts S der beiden Graphen erhält man, indem man die Funktionsterme gleich setzt.
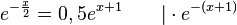
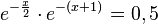
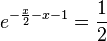
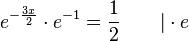
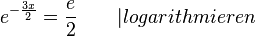
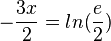
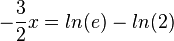
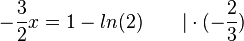
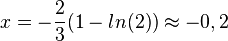
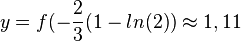 , also S(-0,2; 1,11) (näherungsweise, aber genügend genau!)
, also S(-0,2; 1,11) (näherungsweise, aber genügend genau!)
Den Schnittwinkel zwischen beiden Graphen erhält man, indem man den Schnittwinkel der Tangenten in S an Gf und Gg bestimmt. Dazu muss man nicht die Tangetengleichungen aufstellen. Es reicht, wenn man die Steigungen in S kennt, denn es ist 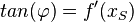 .
.
Man berechnet 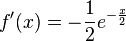 und
und 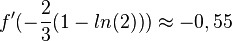 .
.
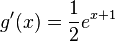 und
und 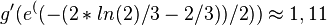 .
.
Für  ist
ist 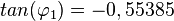 und
und 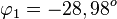 und
und
für  ist
ist 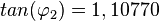 und
und 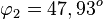 .
.
Damit ist 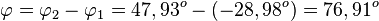 .
.
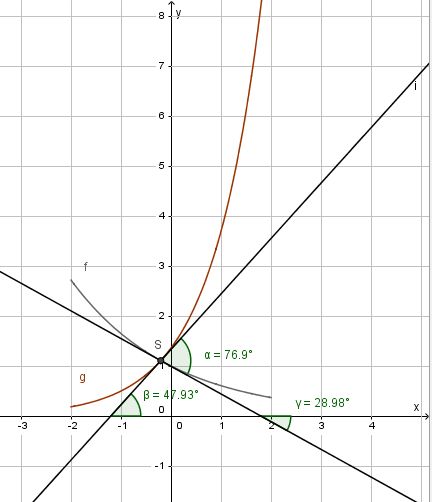
b) Die Tangente in A soll parallel zu einer Geraden h mit Steigung - 0,5 sein. Also ist f'(xA) = - 0,5.
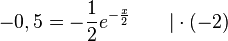
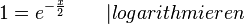
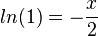 ergibt
ergibt 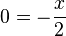 und
und 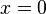 .
.
A(0;1) 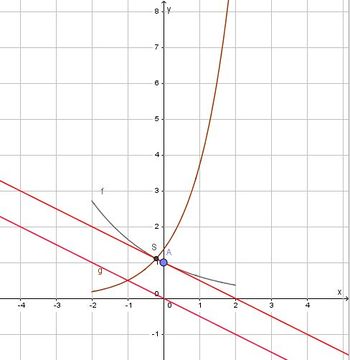
Die Tangente in B soll senkrecht zu einer Geraden k mit Steigung -2 sein. Die Tangente in B an Gg hat dann die Steigung 0,5. Also ist g'(xB) = 0,5.
Zwei Geraden g1: y = m1x+t1 und g2: y = m2x + t2 stehen senkrecht zueinander, wenn m1· m2 = -1 ist.
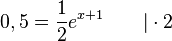
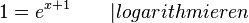
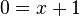 ergibt
ergibt 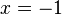
Buch S. 153 / 14
Graph 1 gehört zu Funktion f (f ist die einzige Funktion mit D = R+. Außerdem kann man den Funktionsterm vereinfachen. Es ist f(x) = 2xeln(x)=2x2 und der Graph ist eine halbe Parabel.)
Graph 2 gehört zu Funktion d (d hat bei x = 0 eine Polstelle. )
Graph 3 gehört zu Funktion a (ex wird um den Faktor 2 in y-Richtung gestreckt, ebenso in x-Richtung, also ist der Verlauf fast wie bei der "e-Funktion" durch (0;2).)
Graph 4 gehört zu Funktion b (-ex ist ex an der x-Achse gespiegelt und wird um 3 nach oben verschoben.)
Graph 5 gehört zu Funktion c (c ist die einzig verbleibende Funktion mit c(0) = 2.)
Buch S. 152 / 9
Zuerst zeichnet man den Sachverhalt.
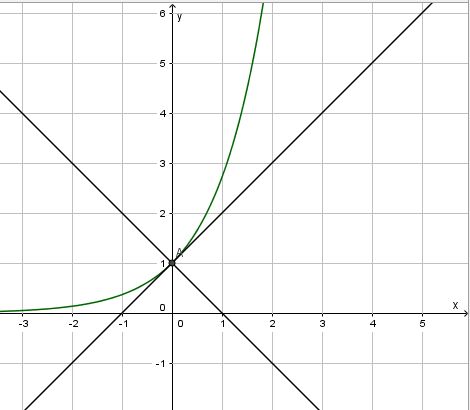
Es ist f'(0) = 1, also ist die Steigung m = 1 der Tangente in (P0;1). Die Tangente hat dann die Gleichung y = x + 1. Sie schneidet die x-Achse in A(-1;0).
Die Normale zur Tangente in P hat dann die Steigung m = -1 und sie hat die Gleichung y = -x +1. Sie schneidet die x-Achse in B(1;0).
Buch S. 152 / 12
a) Die Koordinaten des Schnittpunkts B liest man gleich aus dem Diagramm ab, da beide Graphen sich bei x = 0 schneiden. Es ist B(0;1).
Die x-Koordinate von A erhält man durch Lösen der Gleichung 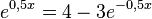 .
.
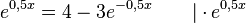

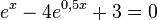
Substituiert man 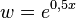 , dann man hat die quadratische Gleilchung
, dann man hat die quadratische Gleilchung 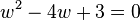 zu lösen. Es ist
zu lösen. Es ist 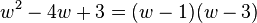 und daher hat die Gleichung
und daher hat die Gleichung 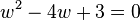 die zwei Lösungen
die zwei Lösungen 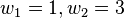 . Die Lösung
. Die Lösung 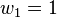 führt beim Resubstituieren auf
führt beim Resubstituieren auf 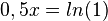 , also
, also 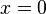 . (Lösung für B!)
. (Lösung für B!)
Die zweite Lösung 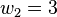 führt beim Resubstituieren auf
führt beim Resubstituieren auf 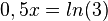 und
und 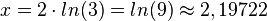 . Also ist A(ln9; 3).
. Also ist A(ln9; 3).
b) Es ist S(a; e0,5a) und T(a;4-3e-0,5a) und die Länge der Strecke [ST] ist 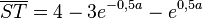 (T liegt über S, also ist bei yT - yS die Differenz positiv).
(T liegt über S, also ist bei yT - yS die Differenz positiv).
Betrachtet man nun die Funktion 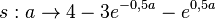 für
für ![a \in [0;ln(9)]](/images/math/6/8/3/683526e7906cfa2c08a68415cb17f301.png) , dann muss man das Maximum von s finden. Dazu setzt man die
, dann muss man das Maximum von s finden. Dazu setzt man die 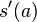 gleich 0 und erhält bei VZW +/- das gesuchte a.
gleich 0 und erhält bei VZW +/- das gesuchte a.
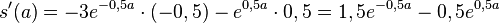
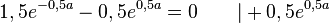
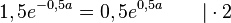
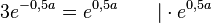
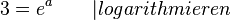
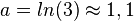
Lässt man sich mit GeoGebra die Graphen von s und s' zeichnen, dann hat man dieses Bild:
Buch S. 154 / 18
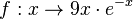 mit D = R.
mit D = R.
a) f(0) = 9\cdot 0 \cdot e0 = 0, also ist (0;0) ein Punkt von Gf.
b) Es ist 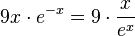 und nach dem Grenzwert in der Merkhilfe für r = 1 ist
und nach dem Grenzwert in der Merkhilfe für r = 1 ist 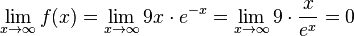
Für den Grenzwert 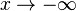 ist
ist 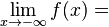 "
" 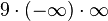 "
"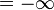
c) Es ist 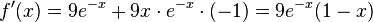
Da stets 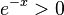 ist, ist
ist, ist 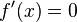 für 1 - x = 0 und x = 1.
für 1 - x = 0 und x = 1.
Da y = 1 - x eine fallende Gerade mit Nullstelle x = 1 ist, ist dort der VZW +/- und damit ist bei x = 0 ein Maximum, Gf hat in (1; ) einen Hochpunkt.
) einen Hochpunkt.
e) Das Bild zu dieser Aufgabe schaut so aus:
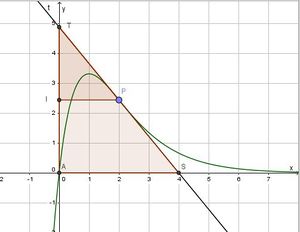
Aufstellen der Gleichung der Tangente:
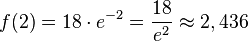 .
.
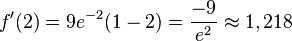 .
.
Ansatz: 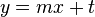 mit
mit 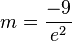 und
und 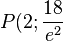 erhält man
erhält man
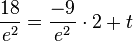
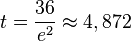
Die Gleichung der Tangente t ist 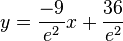 .
.
Der Schnittpunkt mit der y-Achse ist 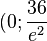 ), der Schnittpunkt mit der x-Achse ist (4;0)
), der Schnittpunkt mit der x-Achse ist (4;0)
Der Flächeninhalt 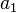 des Dreiecks TIP ist
des Dreiecks TIP ist 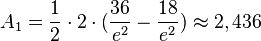
Der Flächeninhalt 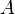 des Dreiecks OST ist
des Dreiecks OST ist 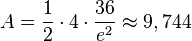
Das Flächenverhältnis ist 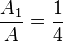 , also nimmt die Fläche des Dreicks TIP 25% der Fläche des Dreiecks OST ein.
, also nimmt die Fläche des Dreicks TIP 25% der Fläche des Dreiecks OST ein.
Diese Aufgabe hätte man auch leichter mit dem Strahlensatz lösen können. Die "kleine waagrechte Strecke" [IP] hat die Länge 2, die "große waagrechte Strecke" [OS] hat die Länge 4. Daher ist der Faktor 2 und für das Verhältnis "Fläche kleines Dreieck" : "Fläche großes Dreieck" = 1 : 22 = 1 : 4. Damit hat man das gleiche Ergebnis.
f) Die Situation schaut so aus:
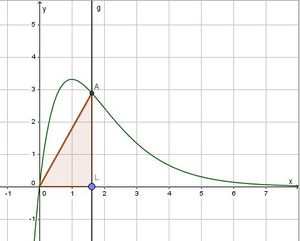
Der Flächeninhalt des Dreiecks OLA ist 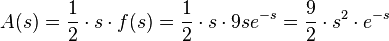
![A'(s) = \frac{9}{2}[2se^{-s}+s^2e^{-s}(-1)]=\frac{9}{2}e^{-s}s(2-s)](/images/math/a/e/8/ae86fa5ca668086e103dc7c83ff73d63.png)
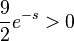 und
und 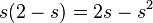 ist der Term einer nach unten geöffneten Parabel mit den Nullstellen 0 und 2. Da die Parabel nach unten geöffnet ist, ist bei s = 0 ein VZW -/+ und bei s = 2 ein VZW +/-. Daher hat A bei x = 2 ein Maximum und es ist
ist der Term einer nach unten geöffneten Parabel mit den Nullstellen 0 und 2. Da die Parabel nach unten geöffnet ist, ist bei s = 0 ein VZW -/+ und bei s = 2 ein VZW +/-. Daher hat A bei x = 2 ein Maximum und es ist 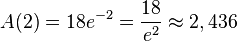 .
.Buch S. 159 / 6
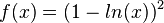 D = R+
D = R+
Gemeinsame Punkte mit der x-Achse: 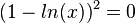 ist erfüllt für
ist erfüllt für 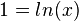 , also
, also 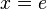 .
.
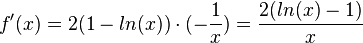
Für x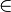 R+ ist der Nenner positiv. Für das Vorzeichen von f' muss man also den Zähler betrachten.
R+ ist der Nenner positiv. Für das Vorzeichen von f' muss man also den Zähler betrachten.
Für x < e ist ln(x) < 1 und ln(x) - 1 < 0, also ist f'(x) < 0 für x < e und f ist in ]0;e] streng monoton abnehmend.
Für x > e ist ln(x) > 1 und ln(x) - 1 > 0, also ist f'(x) > 0 für x > e und f ist in ]e; [ streng monoton zunehmend.
[ streng monoton zunehmend.
Da x = e die einzige Nullstelle von f' ist und einen VZW -/+ hat ist bei (e;0) ein Minimum und Gf hat in (e;0) einen Tiefpunkt.
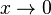 .
.Buch S. 160 / 10
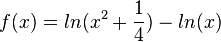 , D = R+
, D = R+
a) Es ist 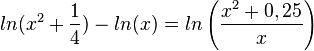
Gemeinsame Punkte mit der x-Achse erhält man, wenn 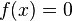 ist. Es ist
ist. Es ist 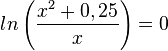 für
für 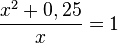 .
.
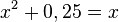 ist eine quadratische Gleichung.
ist eine quadratische Gleichung.
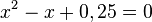 ergibt mit der binomischen Formel
ergibt mit der binomischen Formel 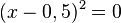 , also ist x = 0,5 (doppelte) Nullstelle von f.
, also ist x = 0,5 (doppelte) Nullstelle von f.
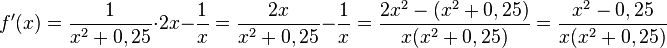
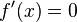 ist
ist 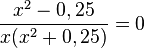 . Da der Nenner für positive x stets positiv ist, muss man nur den Zähler betrachten. Es ist
. Da der Nenner für positive x stets positiv ist, muss man nur den Zähler betrachten. Es ist 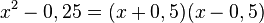 . Der Zähler ist 0 für x = - 0,5 und x = 0,5. -0,5 ist nicht in D, also ist
. Der Zähler ist 0 für x = - 0,5 und x = 0,5. -0,5 ist nicht in D, also ist 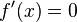 für x = 0,5.
für x = 0,5.
Es ist 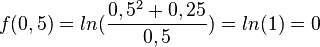
Der Zähler ist eine nach oben geöffnete Parabel, die bei der rechten Nullstelle einen VZW -/+ hat. (Der Nenner ist positiv!). Daher hat f' bei x = 0,5 einen VZW -/+ und f hat bei x = 0,5 ein Minimum, Gf bei (0,5;0) einen Tiefpunkt.
b) ![\lim_{x\to 0+}[ln(x^2+\frac{1}{4}) - ln(x)]=\infty](/images/math/8/f/3/8f35c93b9bb3d1bd559a0409d48ab8b5.png) , da ln(0,25) < 0 und
, da ln(0,25) < 0 und 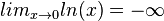 ist.
ist.
Die positive y-Achse ist für 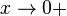 Asymptote.
Asymptote.
![\lim_{x\to \infty}[ln(x^2+\frac{1}{4}) - ln(x)] =\lim_{x\to \infty}ln(\frac{x^2+0,25}{x}=\infty](/images/math/9/7/8/978116f59c7f1c3700f0089f84b2e8f6.png) , da der Grad des Zählerpolynoms 2 ist und damit größer als der Grad des Nennerpolynoms. Der Bruch geht für
, da der Grad des Zählerpolynoms 2 ist und damit größer als der Grad des Nennerpolynoms. Der Bruch geht für  auch gegen
auch gegen  .
.
Der Graph hat für  keine Asymptote.
keine Asymptote.
![\lim_{x\to \infty}[ln(x^2+\frac{1}{4}) - ln(x) -ln(x)]=\lim_{x\to \infty}[ln(x^2+0,25)-2ln(x)=\lim_{x\to \infty}\frac{x^2+0,25}{x^2}=ln(1)=0](/images/math/e/9/9/e99faacae52c6f9b9ac9705815ff1f07.png) , da der Grad des Zählerpolynoms gleich dem Grad des Nennerpolynoms ist. Damit geht der Bruch für
, da der Grad des Zählerpolynoms gleich dem Grad des Nennerpolynoms ist. Damit geht der Bruch für  gegen 1 .
gegen 1 .
Die positive x-Achse ist für  Asymptote.
Asymptote.
d) g(x) = ln(x). Wenn im Argument 2x steht, dann wird der Graph von g um den Faktor 2 in x-Richtung gestaucht.
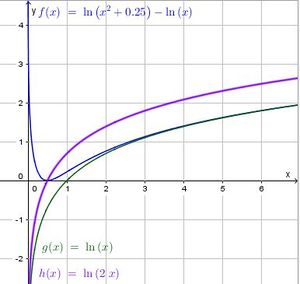
Den Schnittpunkt von Gh und Gf erhält man, wenn man 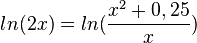 löst. Wenn die beiden Logarithmen gleich sind, müssen auch ihre Argumente gleich sein und man muss die Gleichung
löst. Wenn die beiden Logarithmen gleich sind, müssen auch ihre Argumente gleich sein und man muss die Gleichung 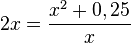 lösen.
lösen.
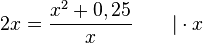
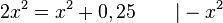
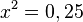
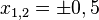
Da D = R+ ist, hat man nur die Lösung x = 0,5 und der Schnittpunkt ist (0,5;0) (x = 0,5 ist Nullstelle, was man in a) gezeigt hat!)
Den Schnittwinkel  erhält man, wenn man
erhält man, wenn man 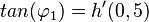 und
und 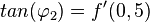 bestimmt und dann
bestimmt und dann 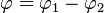 berechnet.
berechnet.
Es ist 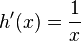 ,
, 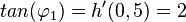 und
und 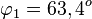 .
.
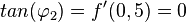 und
und 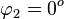 .
.
Also erhält man 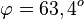 .
.
e)
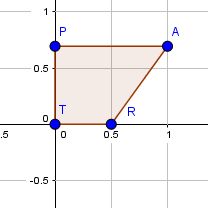
Wenn das Trapez um die x-Ache rotiert entsteht ein Zylinder, bei dem rechts ein Kegel herausgeschnitten ist. Die Grundfläche des Zylinders ist ein Kreis mit Mittelpunkt (0;0) und Radius r = ln(2). Die Höhe des Zylinders ist h = 1, also hat der Zylinder das Volumen 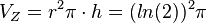 .
.
Der Kegel, der recht herausgenommen wird hat ebenfalls den Radius r = ln(2), aber die Höhe hK = 0,5. Sein Volumen ist 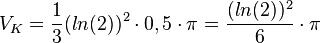 .
.
Damit hat der Rotationskörper das Volumen 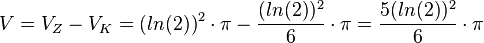 .
.
Die Oberfläche des Rotationskörpers setzt sich aus der Grundfläche des Zylinders, seiner Mantelfläche und der Mantelfläche des Kegel zusammen. Es ist 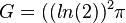 ,
, 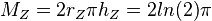 und
und 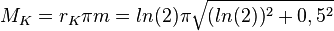 .
.