10c 2012-13: Unterschied zwischen den Versionen
Berny1 (Diskussion | Beiträge) (→Grundwissen wiederholen) |
|||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
=Mathematik= | =Mathematik= | ||
| + | =={{Schrift grün| Stochastik - Wiederholung von Grundbegriffen}}== | ||
| + | * Experiment <br>{{Lösung versteckt|Versuch, bei dem der Ausgang dem Zufall überlassen ist.}} | ||
| + | * Ergebnis<br> {{Lösung versteckt|Ausgang eines einzelnen Experimentes}} | ||
| + | * Ergebnismenge<br> {{Lösung versteckt|Die Menge mit allen möglichen Ergebnissen des Experimentes}} | ||
| + | * Ereignismenge <br>{{Lösung versteckt|Die Menge aller Teilmengen der Ergebnismenge}} | ||
| + | * Ereignis<br> {{Lösung versteckt|ein Element der Ereignismenge}} | ||
| + | * Laplace-Experiment {{Lösung versteckt|Ein Experiment, bei dem jedes Ergebnis von <math>\Omega</math> gleichwahrscheinlich ist.}} | ||
| + | * Sicheres Ereignis<br> {{Lösung versteckt| hat die Wahrscheinlichkeit 100 %}} | ||
| + | * unmögliches Ereignis <br>{{Lösung versteckt|hat die Wahrscheinlichkeit 0 %}} | ||
| + | * Gegenereignis<br> {{Lösung versteckt|hat die Wahrscheinlichkeit 1 - <math>p(Ereignis)</math>}} | ||
| + | |||
| + | {{Aufgabe|[[Datei:Scheibehmxjkl1!.jpg]]<br> | ||
| + | [[Datei:Aufg1s.jpg]] | ||
| + | }} | ||
| + | |||
| + | {{Lösung versteckt|kommt noch}} | ||
| + | <br> | ||
== Grundwissen == | == Grundwissen == | ||
| Zeile 223: | Zeile 240: | ||
== Musikalische Graphen == | == Musikalische Graphen == | ||
* [http://www.didaktik.mathematik.uni-wuerzburg.de/mitarbeiter/anzenhofer/] | * [http://www.didaktik.mathematik.uni-wuerzburg.de/mitarbeiter/anzenhofer/] | ||
| + | *{{#ev:youtube|CRJL1I53mCU|400}} | ||
== Gedanken zur Evolution der Weichtiere == | == Gedanken zur Evolution der Weichtiere == | ||
| Zeile 270: | Zeile 288: | ||
*[http://www.brinkmann-du.de/mathe/aufgabenportal/p3_gr_fkt_t_03/p3_gr_fkt_t_03.htm Übungen Polynomdivision] | *[http://www.brinkmann-du.de/mathe/aufgabenportal/p3_gr_fkt_t_03/p3_gr_fkt_t_03.htm Übungen Polynomdivision] | ||
*[http://www.brinkmann-du.de/mathe/aufgabenportal/p3_gr_fkt_024/p3_gr_fkt_024.htm Übungen Polynomdivision] | *[http://www.brinkmann-du.de/mathe/aufgabenportal/p3_gr_fkt_024/p3_gr_fkt_024.htm Übungen Polynomdivision] | ||
| + | |||
| + | ==Grundwissen== | ||
| + | |||
| + | [[Grundlegende_Kenntnisse_in_Mathematik|Was man am Ende der 10. Klasse wissen sollte]] | ||
Aktuelle Version vom 2. Juli 2013, 13:39 Uhr
Inhaltsverzeichnis |
Mathematik
Stochastik - Wiederholung von Grundbegriffen
- Experiment
- Ergebnis
- Ergebnismenge
- Ereignismenge
- Ereignis
- Laplace-Experiment
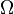gleichwahrscheinlich ist.- Sicheres Ereignis
- unmögliches Ereignis
- Gegenereignis
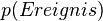
30px Aufgabe
|
Grundwissen
Grundlegende Funktionen Zusammenstellung vom Gymnasium Stein== Kreis- und Kreisteile - Pi-Bestimmung
Aufgaben:
|
|
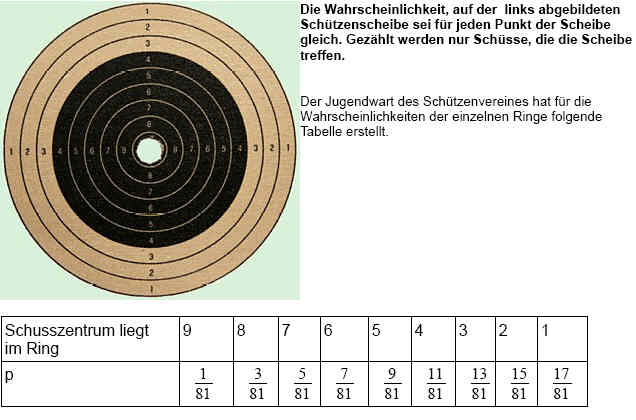
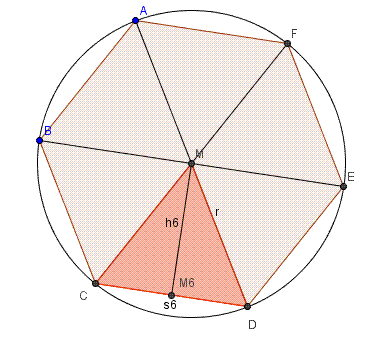
Um die Kreiszahl pi zu bestimmen ist eine Methode einem Kreis reguläre Vielecke ein-/umzubeschreiben wobei mit wachsender Eckenzahl der Umfang des Vielecks gegen den Kreisumfang bzw. die Fläche des Vielecks gegen die Kreisfläche geht im Sinne eines Grenzwertes. Aus dem der Vielecksfläche und dem Quadrat des Radius ergeben sich die (immer genauer werdenden) Näherungswerte für PI. Macht man dies für ein- und umbeschreibene Vielecke, so erhält man eine Intervallschachtelung. |
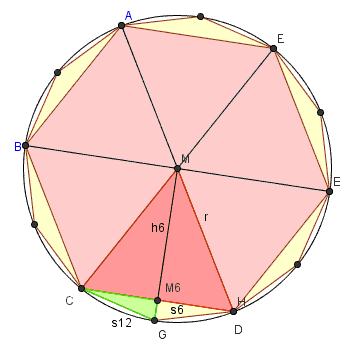
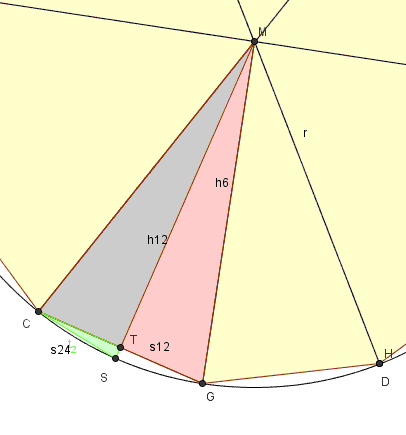
Im folgenden wollen wir ausgehend vom regulären 6-Eck die Flächen des 12-Ecks und des 24-Ecks bestimmen und Näherungswerte für pi berechnen.
|
|
|
Lösung:
|
|
|
Lösung:
|
|
|
Geschichte
Andere Methoden zur Bestimmung der Kreiszahl
Links
Einen ersten Überblick über die Vielfalt der Methoden pi zu bestimmen liefert
Aufgaben
30px Aufgabe
|
Konstruktion:
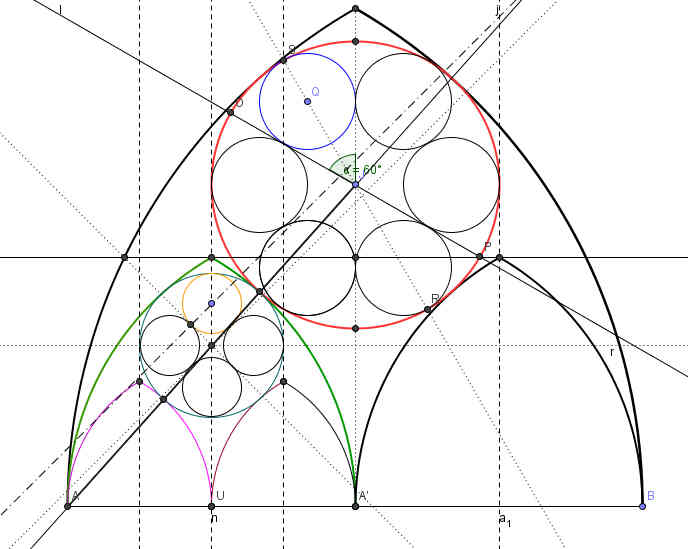
Überlege:
1. Wie groß sind die Radien der inneren gotischen Bögen?
2. Wie groß sind die Radien der Kreise in den Spitzen der gotischen Bögen?
3. Was für Winkel schließen die Tangenten an die Kreise innerhalb der Kreise unter 2 ein?
30px Aufgabe
|
Die Kugel
Aufgaben zum Kugelvolumen und Kugeloberfläche
30px Aufgabe
Überlege Dir sinnvolle Aufgaben zum Berliner Fernsehturm! |
Geometrie am Einheitskreis {von M10}
Das Bogenmaß
Polarkoordinaten
Trigonometrie am Einheitskreis
Arbeitsblätter - bearbeite in der rechten Spalte "Trigonometrie III" den Abschnitt "Der Einheitskreis".
Sinus- und Kosinuswerte am Einheitskreis
Sinus- und Kosinussatz {von M10}
Herleitung des Sinussatzes und Standardaufgabe
Der Sinussatz interaktiv mit Berechnungen
Veranschaulichung des Kosinussatzes
Der Kosinussatz
interaktive Übung
Der Kosinussatz als Verallgemeinerung des Satzes von Pythagoras
Beispielaufgabe zum Sinussatz, Kosinussatz
Einfache Aufgaben mit Lösungen, Aufgaben
Aufgaben und noch mehr Aufgaben und Hinweise zum Vorgehen.
Berechnungen am allgemeinen Dreieck
Sinus- und Kosinusfunktion
Die Sinusfunktion am Einheitskreis
Die allgemeine Sinusfunktion mit Parametern
Lernpfad Trigonometrische Funktionen
Noch ein Lernpfad zu trigonometrischen Funktionen
Experimentelle Mathematik
Musikalische Graphen
Gedanken zur Evolution der Weichtiere
Informationen
Merkhilfe
Die aktualisierte Fassung der Merkhilfe steht auf den Seiten des ISB unter [4] zum Download bereit.
Länderübergreifendes Abitur
Musteraufgabe mit Zusatzinformationen
CAS-Abitur - traditionelles Abitur
Matheabi
unterscheidet sich nur in Geringfügigkeiten vom
CAS-Matheabi
CASIO-Class Pad
Die pdf-Datei kann im Adobe-Reader nach Stichworten durchsucht werden. Also nicht vor der Seitenzahl erschrecken°
- Der Class-Pad im Matheabi von Niedersachsen
- Anwendungsbeispiele
- Arbeitsblätter
- Abeitsblätter von CASIO
Kostenlose Software zum Download CASIO Classpad 330 90-Tage Testversion Download
Grundwissen wiederholen
Kegel, Zylinder, Pyramide - Prinzip von Cavalieri
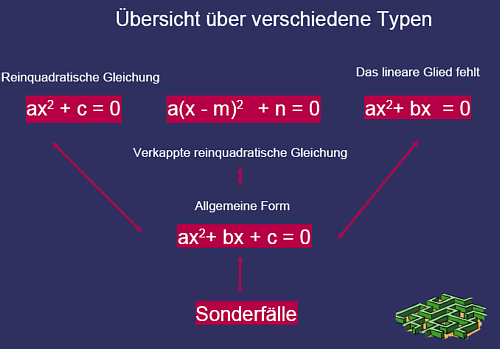
Quadratische Gleichungen geschickt lösen
