2m14.2020: Unterschied zwischen den Versionen
| (4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Hier noch die Überlegungen zur Aufgabe 136/15c: | Hier noch die Überlegungen zur Aufgabe 136/15c: | ||
| − | [[Datei:2m14-20200313.pdf | + | [[Datei:2m14-20200313.pdf|Nachtrag zur Aufgabe 136/15c]] |
| + | Diese Überlegungen in der pdf-Datei habe ich aufgeschrieben, da ich am Ende der Stunde doch etwas gestutzt hatte. Von jeder Punkt im Raum kann man ein Lot auf eine Gerade, die den Punkt nicht enthält machen. Hier war es aber so, dass die in der Aufgabe angegebene Gleichung etwas anderes wissen wollte. Ich hoffe ich habe das ausführlich dargelegt. | ||
| − | + | Es wäre schön, wenn Sie als '''"Hausaufgabe" S. 144/1''' machen. Setzen Sie hierzu, wie wir es im Unterricht gemacht haben, die Geradengleichung in die Normalenform der Ebenengleichung ein und betrachten das Ergebnis. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | Es wäre schön, wenn Sie als "Hausaufgabe" S. 144/1 machen. Setzen Sie hierzu, wie wir es im Unterricht gemacht haben, die Geradengleichung in die Normalenform der Ebenengleichung ein und betrachten das Ergebnis. | + | |
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Bemerkung: Ich verwende statt griechischer Buchstaben deutsche, da sich das leichter schreiben lässt. | Bemerkung: Ich verwende statt griechischer Buchstaben deutsche, da sich das leichter schreiben lässt. | ||
| − | 1a) 2(-2+k) + (2-k) + 2(1+4k)-5 = 0 hat Lösung k = 5/9, also schneidet die Gerade g die Ebene E im Punkt <math>S(-1\frac{4}{9}; 1\frac{4}{9}; | + | 1a) 2(-2+k) + (2-k) + 2(1+4k)-5 = 0 hat Lösung k = 5/9, also schneidet die Gerade g die Ebene E im Punkt <math>S(-1\frac{4}{9}; 1\frac{4}{9}; 3 \frac{2}{9})</math><br> |
b) 6(6k)-2(-4+12k)-3(4k)-8=0 hat Lösung 0 = 0. Die Gleichung ist allgemeingültig, also liegt die Gerade g in der Ebene E.<br> | b) 6(6k)-2(-4+12k)-3(4k)-8=0 hat Lösung 0 = 0. Die Gleichung ist allgemeingültig, also liegt die Gerade g in der Ebene E.<br> | ||
c) 4-2k+2=0 hat als Lösung k = 3, also schneidet die Gerade g die Ebene E im Punkt S(-1;-2;4).<br> | c) 4-2k+2=0 hat als Lösung k = 3, also schneidet die Gerade g die Ebene E im Punkt S(-1;-2;4).<br> | ||
| Zeile 38: | Zeile 18: | ||
Die Gleichung -2(1+k) - 2k + 1-k + 6=0 hat die Lösung k = 1, also schneidet die Gerade g die Ebene E im Punkt S(2;-2;0).<br> | Die Gleichung -2(1+k) - 2k + 1-k + 6=0 hat die Lösung k = 1, also schneidet die Gerade g die Ebene E im Punkt S(2;-2;0).<br> | ||
e) Normalform: x<sub>1</sub>+2x<sub>3</sub>=0<br> | e) Normalform: x<sub>1</sub>+2x<sub>3</sub>=0<br> | ||
| − | Die Gleichung 2-2k +2(3+k)=0 lässt sich umformen zu 6 = 0, also führt zu einer falschen Aussage. Damit ist die Gerade g (echt) parallel zur Ebene E. | + | Die Gleichung 2-2k +2(3+k)=0 lässt sich umformen zu 6 = 0, also führt zu einer falschen Aussage. Damit ist die Gerade g (echt) parallel zur Ebene E. <br> |
f) Normalform: x<sub>2</sub>+3x<sub>3</sub>-5=0<br> | f) Normalform: x<sub>2</sub>+3x<sub>3</sub>-5=0<br> | ||
3+k + 3(5+4k)-5 = 0 hat die Lösung k = -1, also schneidet die Gerade g die Ebene E im Punkt S(-1;2,1).<br> | 3+k + 3(5+4k)-5 = 0 hat die Lösung k = -1, also schneidet die Gerade g die Ebene E im Punkt S(-1;2,1).<br> | ||
| − | Sie erhalten den Schnittpunkt S, indem Sie den Wert von k in die Geradengleichung einsetzen. | + | ''Sie erhalten den Schnittpunkt S, indem Sie den Wert von k in die Geradengleichung einsetzen.'' |
}} | }} | ||
Aktuelle Version vom 16. März 2020, 11:40 Uhr
Hier noch die Überlegungen zur Aufgabe 136/15c:
Diese Überlegungen in der pdf-Datei habe ich aufgeschrieben, da ich am Ende der Stunde doch etwas gestutzt hatte. Von jeder Punkt im Raum kann man ein Lot auf eine Gerade, die den Punkt nicht enthält machen. Hier war es aber so, dass die in der Aufgabe angegebene Gleichung etwas anderes wissen wollte. Ich hoffe ich habe das ausführlich dargelegt.
Es wäre schön, wenn Sie als "Hausaufgabe" S. 144/1 machen. Setzen Sie hierzu, wie wir es im Unterricht gemacht haben, die Geradengleichung in die Normalenform der Ebenengleichung ein und betrachten das Ergebnis.
Bemerkung: Ich verwende statt griechischer Buchstaben deutsche, da sich das leichter schreiben lässt.
1a) 2(-2+k) + (2-k) + 2(1+4k)-5 = 0 hat Lösung k = 5/9, also schneidet die Gerade g die Ebene E im Punkt 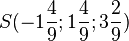
b) 6(6k)-2(-4+12k)-3(4k)-8=0 hat Lösung 0 = 0. Die Gleichung ist allgemeingültig, also liegt die Gerade g in der Ebene E.
c) 4-2k+2=0 hat als Lösung k = 3, also schneidet die Gerade g die Ebene E im Punkt S(-1;-2;4).
d) Die Normalform lässt sich schreiben als -2x1+x2+x3+6=0.
Die Gleichung -2(1+k) - 2k + 1-k + 6=0 hat die Lösung k = 1, also schneidet die Gerade g die Ebene E im Punkt S(2;-2;0).
e) Normalform: x1+2x3=0
Die Gleichung 2-2k +2(3+k)=0 lässt sich umformen zu 6 = 0, also führt zu einer falschen Aussage. Damit ist die Gerade g (echt) parallel zur Ebene E.
f) Normalform: x2+3x3-5=0
3+k + 3(5+4k)-5 = 0 hat die Lösung k = -1, also schneidet die Gerade g die Ebene E im Punkt S(-1;2,1).


