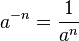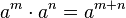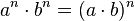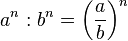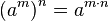M8 Potenzen mit ganzzahligen Exponenten: Unterschied zwischen den Versionen
| Zeile 236: | Zeile 236: | ||
Aber man folgendes machen: <math>\frac{x^{-1} - y^{-1}}{x-y}=\frac{\frac{1}{x}-\frac{1}{y}}{x-y}=\frac{\frac{y}{xy}-\frac{x}{xy}}{x-y}=\frac{\frac{y-x}{xy}}{x-y}=\frac{y-x}{xy\cdot (x-y)} =\frac{-(x-y)}{xy\cdot(x-y)}=\frac{1}{xy}=(xy)^{-1}</math> <br> | Aber man folgendes machen: <math>\frac{x^{-1} - y^{-1}}{x-y}=\frac{\frac{1}{x}-\frac{1}{y}}{x-y}=\frac{\frac{y}{xy}-\frac{x}{xy}}{x-y}=\frac{\frac{y-x}{xy}}{x-y}=\frac{y-x}{xy\cdot (x-y)} =\frac{-(x-y)}{xy\cdot(x-y)}=\frac{1}{xy}=(xy)^{-1}</math> <br> | ||
Und das schaut doch einfacher aus! :-) }} | Und das schaut doch einfacher aus! :-) }} | ||
| + | |||
| + | {{Aufgaben-blau|6|2=Potenzen mit negativen Exponenten treten auch oft in der Physik bei den Einheiten auf und ermöglicht eine neue Schreibweise für Einheiten.<br> | ||
| + | Buch S. 136 / 7 }} | ||
| + | |||
| + | {{Lösung versteckt|1=a) <math>m\cdot s^{-1}=\frac{m}{s}</math> ist die Einheit der Geschwindigkeit.<br> | ||
| + | b) <math>km \cdot h^{-1}=\frac{km}{h}</math> ist auch eine Einheit der Geschwindigkeit.<br> | ||
| + | c) <math>N \cdot m^{-1}=\frac{N}{m}</math> ist die Einheit der Federkonstante D.<br> | ||
| + | d) <math>N \cdot m^{-2}=\frac{N}{m^2}</math> ist die Einheit des Drucks p. <br> | ||
| + | e) <math>N \cdot kg^{-1}=\frac{N}{kg}</math> ist die Einheit des Ortsfaktors g und auch die Einheit der Beschleunigung a.<br> | ||
| + | f) <math>g \cdot cm^{-3}=\frac{g}{cm^3}</math> ist die Einheit der Dichte.}} | ||
Version vom 15. Mai 2020, 17:30 Uhr
In Physik oder Chemie gibt es eine wissenschaftliche Schreibweise für Größen. Man gibt die Größe als Zahl mit Einheit und oftmals ist die Zahl mit Zehnerpotenzen geschrieben. Dies macht man gerne, da man sonst den Zahlenwert nur sehr schwer lesen kann. Zum Beispiel ist die Masse der Erde m = 6000000000000000000000000 kg. Man kann die Zahl durch Dreierbündel der Nullen etwas übersichtlicher gestalten m = 6 000 000 000 000 000 000 000 000 kg. Aber sehr viel einfacher wird es dadurch auch nicht. Daher schreibt man gerne m = 6·1024 kg. Diese Schreibweise schaut doch wenn man ihre Bedeutung kennt sehr viel einfacher aus.
Was heißt 1024?
1024 ist eine Potenz 10 ist die Basis 24 der Exponent. Eine Potenz ist eine Abkürzung für ein Produkt mit lauter gleichen Faktoren.
Hier ist 1024=10·10·10·10·10·10·10·10·10·10·10·10·10·10·10·10·10·10·10·10·10·10·10·10. Der Faktor 10 kommt 24 mal vor.
30px Merke
an ist eine Potenz, a ist die Basis, n der Exponent. |
Potenzen kennst du schon. Meist ist die Basis eine natürliche Zahl, ebenso der Exponent.
Was macht man aber, wenn man eine sehr kleine Zahl hat? Der Atomdurchmesser ist circa 0,0000000001m. Dies ist auch sehr unübersichtlich zu lesen. Kann man diese Zahl auch mit einer Zehnerpotenz schreiben?
|
In dieser Tabelle hat man mit der Zehnerpotenz 105 angefangen. 105 wird durch 10 dividiert und man erhält in der nächsten Zeile 104. 104 wird durch 10 dividiert und man erhält in der nächsten Zeile 103. 103 wird durch 10 dividiert und man erhält in der nächsten Zeile 102. 102 wird durch 10 dividiert und man erhält 101. Wie geht es nun weiter? |
30px Merke
Bei diesem Vorgehen dividiert man eine Zehnerpotenz durch 10 und der Exponent verringert sich dabei um 1, also 10n : 10 = 10n-1. |
Macht man dieses Verfahren nun weiter, so erhält man:
| 102 | :10 |
| 101 | :10 |
| 100 | :10 |
| 10-1 | :10 |
| 10-2 | :10 |
| 10-3 | :10 |
| 10-4 | :10 |
| usw. |
Nun hat man plötzlich Potenzen mit negativen Exponenten. In unserem Fall 10-n. Aber die Werte dieser Potenzen kennt man schon. Es ist:
| 102 =100 | :10 |
| 101=10=:10=10 | :10 |
| 100=10:10=1 | :10 |
| 10-1=1:10=0,1 | :10 |
| 10-2=0,1:10=0,01 | :10 |
| 10-3=0,01:10=0,001 | :10 |
| 10-4=0,001:10=0,0001 | :10 |
| usw. |
30px Merke
Also kann man sagen, 10-n ist eine Dezimalzahl mit n Nachkommastellen. Die letzte Nachkommastelle ist 1, alle anderen sind 0. |
Für unseren Atomdurchmesser 0,0000000001m bedeutet dies, dass die Zahl 10 Nachkommastellen hat und die letze Ziffer ist 1, also ist 0,0000000001m = 10-10m.
|
Merke:
Man definiert Potenzen an mit ganzzahligen Exponenten: |
Beispiele
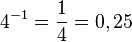
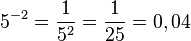
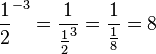
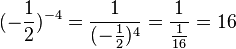
S. 133/1
a) 0,53=0,5·0,5·0,5 = 0,125
0,5-1 = 1/5 = 0,2
(-0,5)-2 = 4
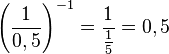
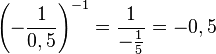
b) 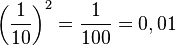
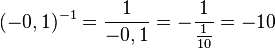
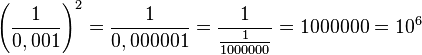
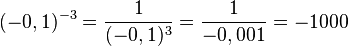
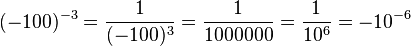
(-0,001)0 = 1
S. 133/4
a) 0,20 + 0,21 + 0,22 + 0,23 + 0,24 = 1 + 0,2 + 0,04 + 0,008 + 0,0016 = 1.2496
a) 149 600 000 km = 1,496·108km
1,52143·108km
1,47057·108km
1,2756·104km = 1,2756·107m
1,2713·104km
5,974·1021t =5,974·1024kg
1,087·1012km3
5,101·108km2
b) 9,1·10-28g = 9,1·10-31kg
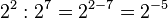 , also allgemein
, also allgemein 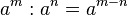 auch für negative Exponenten.
auch für negative Exponenten.
|
Merke:
Auch für Potenzen mit negativen Exponenten gelten weiterhin die Potenzgesetze. Potenzen mit gleicher Basis: Potenzen mit gleichem Exponenten Potenzieren einer Potenz Beachte: Die Potenzgesetze gelten nur beim Multiplizieren und Dividieren von Potenzen. |
Zwei Potenzen mit gleicher Basis werden multipliziert, indem man die Basis beibehält und die Exponenten addiert.
Zwei Potenzen mit gleicher Basis werden dividiert, indem man die Basis beibehält und die Exponenten subtrahiert.
Zwei Potenzen mit gleichem Exponenten werden multipliziert, indem man die Basen multipliziert und den Exponenten beibehält.
Zwei Potenzen mit gleichem Exponenten werden dividiert, indem man die Basen dividiert und den Exponenten beibehält.
Beispiele:
1. x5 · x4 = x5+4 = x9
x5 · x -4 = x 5-4 = x1 = x
4x -5 · x -4 = 4x-5-4 = 4x-9
2. x5 : x -4 = x 5-(-4) = x5+4 = x9
2x -4 : x -7 = 2x-4-(-7) = 2x-4+7 = 2x3
3. (x -2)3 = x -2·3 = x -6
(x -4) -3 = x -4·(-3) = x12
(0,5x -3) -2 = 0,5 -2x -3·(-2) = 4x6
4. a1-m · 21-m = (2a)1-m
(ab)6 : (ac)5 = 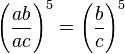
(abc)5 · (-abc)2m+1 = (abc)5 · [-(abc)2m+1] = - (abc)5+2m+1 = - (abc)6+2m
Beachte, dass der Exponent 2m+1 immer ungerade ist. Eine negative Zahl hoch einer ungeraden Zahl ist negativ. Daher wird das - vor die Potenz geschrieben.
5. 5004 = (5 · 100)4 = 54 · 1004 = 625 · (102)4 = 625 · 108 = 6,25 · 1010
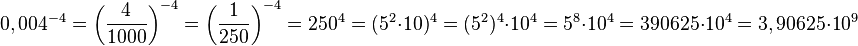
Wenn du mit den Beispielen klar gekommen bist, dann schau dir noch dieses Video an.
Die letze Potenz 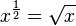 lernst du in der 9. Klasse kennen. Da gibt es dann auch wieder Potenzgesetze.
lernst du in der 9. Klasse kennen. Da gibt es dann auch wieder Potenzgesetze.
S. 135/1
a) -216 <br<
b) -81
c) 16
d) -1000
e) 45
f) 225
g) 135
h) -19
i) 1
j) 4
k) 26 = 64
l) 33 = 27
m) 1,5
n) 1
o) 8
p) 4 + 2,5 - 6,6 = 0
q) 3
S. 135/2
a) y6
b) x-1
c) x-2
d) x-8 · x9 = x
e) 6a-3
f) -x4
S. 135/3
a) 212
b) 2-12 =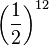
c) 2-12=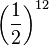 = 0,512
= 0,512
d) 212
e) 2-5 =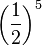 = 0,55
= 0,55
S. 135/4
a) 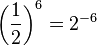
b) 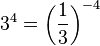
c) 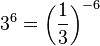
d) 210 = 0,5-10
e) 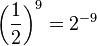
g) 104 = 0,1-4
S. 135/5
a) x4
b) y-3
c) x0 = 1
d) x -4 y4
e) Hier stehen in Zähler und Nenner Differenzen. Man kann Zähler und Nenner nicht in ein Produkt umwandeln. :-(
Aber man folgendes machen: 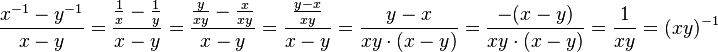
a) 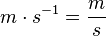 ist die Einheit der Geschwindigkeit.
ist die Einheit der Geschwindigkeit.
b) 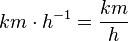 ist auch eine Einheit der Geschwindigkeit.
ist auch eine Einheit der Geschwindigkeit.
c) 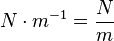 ist die Einheit der Federkonstante D.
ist die Einheit der Federkonstante D.
d) 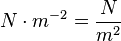 ist die Einheit des Drucks p.
ist die Einheit des Drucks p.
e) 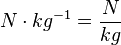 ist die Einheit des Ortsfaktors g und auch die Einheit der Beschleunigung a.
ist die Einheit des Ortsfaktors g und auch die Einheit der Beschleunigung a.
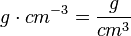 ist die Einheit der Dichte.
ist die Einheit der Dichte.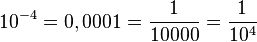
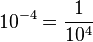 oder allgemein
oder allgemein 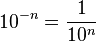

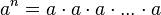 (mit n gleichen Faktoren a),
(mit n gleichen Faktoren a),
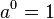 und
und