M9 Quadratische Funktionen und lineare Gleichungssysteme: Unterschied zwischen den Versionen
| Zeile 15: | Zeile 15: | ||
Also erhält man als Parabelgleichung <math>y=-\frac{1}{48}(x-96)^2+192</math><br> | Also erhält man als Parabelgleichung <math>y=-\frac{1}{48}(x-96)^2+192</math><br> | ||
Man bringt diese Gleichung noch auf die normale Form <math>-\frac{1}{48}(x^2-192x+ 96^2)+192=-\frac{1}{48}x^2+4x -192+192=-\frac{1}{48}x^2 + 4x</math>, also <math>y=-\frac{1}{48}x^2 + 4x</math>. }} | Man bringt diese Gleichung noch auf die normale Form <math>-\frac{1}{48}(x^2-192x+ 96^2)+192=-\frac{1}{48}x^2+4x -192+192=-\frac{1}{48}x^2 + 4x</math>, also <math>y=-\frac{1}{48}x^2 + 4x</math>. }} | ||
| + | |||
| + | Wenn der Scheitel S und eine Nullstelle gegeben ist kann man mit der Scheitelform relativ leicht eine Parabelgleichung angeben. | ||
| + | |||
| + | Was macht man aber, wenn man nur drei Punkte A, B und C gegeben hat. | ||
| + | |||
| + | 1. Beispiel: Gegeben sind die drei Punkte A(0;0), B(2;4) und C(3;9).<br> | ||
| + | Da du fit bei den quadratischen Funktionen bist sieht du sofort, dass die Punkte auf dem Graph der Funktion <math>f:x\rightarrow x^2</math>, der Normalparabel liegen.<br> | ||
| + | |||
| + | Wenn du es nicht sofort sieht, dann mach folgende Überlegung mit.<br> | ||
Version vom 9. Februar 2021, 07:58 Uhr
In der 8. Klasse hast du gelernt lineare Gleichungssysteme von zwei Gleichungen mit zwei Unbekannten zu lösen. Schau dir zur Wiederholung wie das geht dieses Video an:
Wir brauchen diese Verfahren um folgendes Problem zu lösen. Wir haben Punkte und wollen schauen, ob die Punkte auf einer Parabel liegen.
Ein Tourist schreibt aus St. Louis (USA) eine Ansichtskarte nach Hause.
Er beschreibt die besonderheit des Gateway Arch, dass die Breite unten am Fuß genauso groß ist wie die Höhe des Bauwerks, nämlich 192m. Und es erinnert ihn sehr an eine Parabel.
Kannst du eine Parabelgleichung für den Bogen angeben?
Legt man in den linken unteren Fußpunkt den Ursprung eines Koordinatensystems, so ist der rechte Fußpunkt bei (192;0) und der Scheitel S(96;192).
Mit der Scheitelform der Parabelgleichung erhält man sofort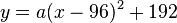 
.
Nun muss man noch a bestimmen. Dazu verwendet man den linken Fußpunkt (0;0). Setzt man die Koordinatenwerte in die Gleichung ein, dann hat man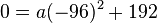 
und es ergibt sich 
.
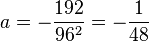Also erhält man als Parabelgleichung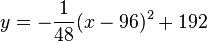 
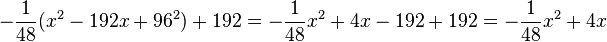, also 
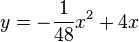.Wenn der Scheitel S und eine Nullstelle gegeben ist kann man mit der Scheitelform relativ leicht eine Parabelgleichung angeben.
Was macht man aber, wenn man nur drei Punkte A, B und C gegeben hat.
1. Beispiel: Gegeben sind die drei Punkte A(0;0), B(2;4) und C(3;9).
Da du fit bei den quadratischen Funktionen bist sieht du sofort, dass die Punkte auf dem Graph der Funktion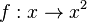 
, der Normalparabel liegen.
Wenn du es nicht sofort sieht, dann mach folgende Überlegung mit.
