M9 Wiederholung in den Faschingsferien: Unterschied zwischen den Versionen
(→Quadratische Funktionen) |
(→Quadratische Funktionen) |
||
| Zeile 32: | Zeile 32: | ||
{{Merke|1=Aus dem Graphen kann man meistens die Parabelgleichung ablesen.<br> | {{Merke|1=Aus dem Graphen kann man meistens die Parabelgleichung ablesen.<br> | ||
Vorgehen: 1. Scheitel ablesen --> x<sub>S</sub> und y<sub>S</sub> für die Scheitelform. <br> | Vorgehen: 1. Scheitel ablesen --> x<sub>S</sub> und y<sub>S</sub> für die Scheitelform. <br> | ||
| − | 2. Von S aus waagrecht 1 nach rechts oder 1 nach links und dann senkrecht bis zur Parabel --> die Länge der senkrechten Strecke ist a.<br> | + | 2. Von S aus waagrecht 1 nach rechts oder 1 nach links und dann senkrecht bis zur Parabel (türkis) --> die Länge der senkrechten Strecke ist a (orange).<br> |
3. a, x<sub>S</sub> und y<sub>S</sub> in die Scheitelform <math>f(x) = a(x-x_S)^2+y_S</math> einsetzen.<br> | 3. a, x<sub>S</sub> und y<sub>S</sub> in die Scheitelform <math>f(x) = a(x-x_S)^2+y_S</math> einsetzen.<br> | ||
4. In der Scheitelform die Klammern auflösen und zusammenfassen. | 4. In der Scheitelform die Klammern auflösen und zusammenfassen. | ||
| Zeile 39: | Zeile 39: | ||
Vorgehen: 1. den Term <math>ax^2+bx+c</math> in die Scheitelform umwandeln <math>f(x) = a(x-x_S)^2+y_S</math> und <math>x_S, y_S, a</math> ablesen.<br> | Vorgehen: 1. den Term <math>ax^2+bx+c</math> in die Scheitelform umwandeln <math>f(x) = a(x-x_S)^2+y_S</math> und <math>x_S, y_S, a</math> ablesen.<br> | ||
2. Im Koordinatensystem S einzeichnen.<br> | 2. Im Koordinatensystem S einzeichnen.<br> | ||
| − | 3. Von S aus waagrecht 1 nach rechts bzw. 1 nach links gehen und dann senkrecht dazu a in y-Richtung antragen. Damit hat man zwei Punkte der Parabel.<br> | + | 3. Von S aus waagrecht 1 nach rechts bzw. 1 nach links gehen und dann senkrecht dazu a in y-Richtung antragen (türkis und orange). Damit hat man zwei Punkte der Parabel.<br> |
4. Wer es genauer haben will, geht von S aus 0,5 waagrecht nach rechts und links und <math>\frac{a}{4}</math> in y-Richtung. --> 2 weitere Punkte der Parabel.<br> | 4. Wer es genauer haben will, geht von S aus 0,5 waagrecht nach rechts und links und <math>\frac{a}{4}</math> in y-Richtung. --> 2 weitere Punkte der Parabel.<br> | ||
Von S aus waagrecht 2 nach rechts und 2 nach links und um 4a in y-Richtung. --> 2 weitere Punkte. <br> | Von S aus waagrecht 2 nach rechts und 2 nach links und um 4a in y-Richtung. --> 2 weitere Punkte. <br> | ||
Version vom 14. Februar 2021, 15:14 Uhr
Die Ferien sollen ja zur Wiederholung und zum Schließen von Wissenlücken genutzt werden.
Daher:
Inhaltsverzeichnis |
Wiederholung aus vorangegangenen Jahrgangsstufen
Wiederholung von Grundwissen aus vorhergehenden Klassen
Auf der Seite des Rhön-Gymnasiums gibt es schöne Zusammenstellungen vom Grundwissen der einzelnen Jahrgangsstufen. Auf der Seite nach unten scrollen bis man bei Grundwissen ankommt.
Grundwissen aller Jahrgangsstufen mit Aufgaben dazu.
Rechnen mit Wurzeln
Das Grundwissen zum Wurzelrechnen ist hier am Anfang zusammengestellt.
Aufgaben mit Lösungen zum Ausdrucken:
Aufgabenblatt 1
Aufgabenblatt 2
Aufgabenblatt 3
Satz des Pythagoras
Binomische Formeln
Aufgabenblatt 1
Aufgabenblatt 2
Quadratische Funktionen
|
Aus dem Graphen kann man meistens die Parabelgleichung ablesen. Umgekehrt kann man für einen quadratischen Term |
Im folgenden Applet kannst du die Werte für xS, yS und a einstellen und am Graphen den Funktionsterm ablesen. Am Graph ist die Scheitelform angegeben, im Fenster eventuell der "normale" Term.
Probiere beide Wege, die in "Merke" angeführt sind aus!
Normalparabel verschieben
Funktionsterme finden und Graphen zeichnen
Quadratische Ergänzung
Die Mitternachtsformel
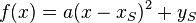 einsetzen.
einsetzen.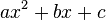 genauso gut die Parabel zeichnen.
genauso gut die Parabel zeichnen.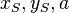 ablesen.
ablesen.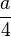 in y-Richtung. --> 2 weitere Punkte der Parabel.
in y-Richtung. --> 2 weitere Punkte der Parabel.
