Ph9 Der freie Fall: Unterschied zwischen den Versionen
| Zeile 63: | Zeile 63: | ||
b) <math>v=4,5\frac{m}{s}</math> ergibt für <math>t = \frac{v}{g}=\frac{4,5\frac{m}{s}}{9,8\frac{m}{s^2}}=0,46s</math> <br> | b) <math>v=4,5\frac{m}{s}</math> ergibt für <math>t = \frac{v}{g}=\frac{4,5\frac{m}{s}}{9,8\frac{m}{s^2}}=0,46s</math> <br> | ||
und für <math>h_0=\frac{1}{2}gt^2=\frac{1}{2}\cdot 9,8\frac{m}{s^2}\cdot (0,46s)^2= 1m</math> }} | und für <math>h_0=\frac{1}{2}gt^2=\frac{1}{2}\cdot 9,8\frac{m}{s^2}\cdot (0,46s)^2= 1m</math> }} | ||
| + | |||
| + | |||
| + | {{Aufgaben-blau|5|2=Wie tief ist der Brunnen? | ||
| + | |||
| + | [[Datei:Nürnberg,_Burg,_Tiefer_Brunnen,_003.jpg|thumb]] | ||
| + | Beim Wandertag geht es nach Nürnberg und bei einer Führung in der Nürnberger Burg kommt man auch zum Brunnenhaus und kann sich den "tiefen Brunnen" ansehen. Ein Theo lässt einen Stein in den Brunnen fallen und stoppt 3,44s für die Zeit, bis er das Auftreffen des Steins hört.<br> | ||
| + | a) Theo berechnet die Tiefe des Brunnens mit der Formel <math>h(t) = \frac{1}{2}gt^2</math>. Welchen Wert für die Tiefe des Brunnens erhält er?<br> | ||
| + | b) Martha wendet zu Theos Rechnung aber ein: "Der Wert kann nicht stimmen, denn er berücksichtigt nicht die Zeit, die der Schall für die Strecke vom Boden des Brunnens bis zu Theos Standort benötigt. Die Gesamtzeit setzt sich aus der Fallzeit des Steins und der Zeit, die der Schall nach oben braucht zusammen." <br> | ||
| + | Wie tief ist der Brunnen, wenn man die Zeit des Schalls mit berücksichtigt?<br> | ||
| + | Die Geschwindigkeit des Schalls in Luft ist <math>v_{Schall}\approx 340\frac{m}{s}</math>. }} | ||
| + | |||
| + | {{Lösung versteckt|1=a) Für den freien Fall eines Körpers kennt man aus der Physik die Formel <math> h = \frac{1}{2}gt^2</math>. Dabei ist g die Erdbeschleunigung <math>g = 9,81\frac{m}{s^2}</math>. <br> | ||
| + | Setzt man die gemessene Zeit t = 3,44s in die Gleichung für h, dann erhält man <math>h=\frac{1}{2}\cdot 9,81\cdot {m}{s^2}\cdot (3,44s)^2=58m</math>. | ||
| + | |||
| + | b) Sophie hat mit ihrem Einwand natürlich Recht. Die gemessene Zeit setzt sich zusammen aus der <br> | ||
| + | * Fallzeit <math>t_{Stein}</math>des Steins und<br> | ||
| + | * der Zeit <math>t_{Schall}</math>, die der Schall vom Boden bis zum Standort <br> | ||
| + | braucht. Es ist <math>3,44s = t_{Stein} + t_{Schall}</math>.<br> | ||
| + | Der Stein und der Schall legen beide jeweils den Weg <math>h</math> zurück. Dabei macht der Stein eine Bewegung mit konstanter Beschleunigung und der Schall eine Bewegung mit konstanter Geschwindigkeit.<br> | ||
| + | Der Stein wird mit konstanter Beschleunigung beschleunigt, dabei ist der zurückgelegte Weg <math>h = \frac{1}{2}gt_{Stein}^2</math>.<br> | ||
| + | Der Schall macht eine Bewegung mit konstanter Geschwindigkeit, dabei ist der zurückgelegte Weg <math>h=c_{Schall}t</math>, wobei <math>c_{Schall} \approx 340\frac{m}{s}</math> ist.<br> | ||
| + | Da in beiden Fällen der gleiche Weg <math>h</math> zurückgelegt wird, kann man die beiden Gleichungen gleich setzen. <br> | ||
| + | <math>\frac{1}{2}gt_{Stein}^2=c_{Schall}t</math><br> | ||
| + | Dies ist eine Gleichung mit zwei Unbekannten <math>t_{Stein}</math> und <math>t_{Schall}</math>.<br> | ||
| + | Von Sophia wissen wir, dass <math>3,44s = t_{Stein} + t_{Schall}</math> ist. Das ist die zweite Gleichung.<br> | ||
| + | Man hat ein Gleichungssystem mit zwei Unbekannten:<br> | ||
| + | (1) <math>\frac{1}{2}gt_{Stein}^2=c_{Schall}t</math><br> | ||
| + | (2) <math>3,44s = t_{Stein} + t_{Schall}</math><br> | ||
| + | Löst man (2) nach <math>t_{Schall}</math> auf und setzt den erhaltenenen Term in (1) ein, dann hat man<br> | ||
| + | <math>\frac{1}{2}gt_{Stein}^2=c_{Schall}(3,44s - t_{Stein})</math><br> | ||
| + | Man erhält eine quadratische Gleichung für <math>t_{Stein}</math>: <math>\frac{1}{2}gt_{Stein}^2+c_{Schall}t_{Stein}-c_{Schall }\cdot 3,44s=0</math><br> | ||
| + | Mit der Lösungsformel erhält man <math>t_{Stein 1,2}=\frac{-c_{Schall} \pm \sqrt {(c_{Schall})^2+4\cdot \frac{1}{2}g\cdot c_{Schall}\cdot 3,44s}}{2\cdot \frac{1}{2}g}= \frac{-340\frac{m}{s} \pm \sqrt {(340\frac{m}{s})^2+4\cdot \frac{1}{2}\cdot 9,81 \frac{m}{s^2} \cdot 340\frac{m}{s}\cdot 3,44s}} {2\cdot \frac{1}{2}9,81\frac{m}{s^2}}</math><br> | ||
| + | Das -Zeichen vor der Wurzel kann man weglassen, da sonst im Zähler etwas Negatives stehen würde und damit die Zeit negativ wäre. Dies kann nicht sein. Also kann man gleich nur mit dem + rechnen. Setzt man die Werte ein, dann erhält man <matsh>t_{Stein}=3,284s<br> und für den Schall <math>t_{Schall}=0,156s</math>.<br> | ||
| + | Damit erhält man für die Tiefe des Brunnens <br> | ||
| + | * bei der Bewegung mit konstanter Beschleunigung des Steins <math>h=\frac{1}{2}\cdot 9,81\frac{m}{s^2}\cdot (3,284s)^2=52,9m</math><br> | ||
| + | * bei der Bewegung des Schalls mit konstanter Geschwindigkeit <math>h=340\ frac{m}{s}\cdot 0,156s=53,0m</math>. }} | ||
Version vom 22. Februar 2021, 18:01 Uhr
1. Der freie Fall ist eine Bewegung mit konstanter Beschleunigung ohne Berücksichtigung der Luftreibung.
2. Beim freien Fall wirkt die Erdanziehungskraft.
3. Die Beschleunigung beim freien Fall ist die Erdbeschleunigung 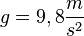 .
.
4. 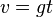 und
und 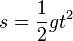 .
.
5. 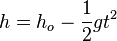 .
.
6. Die Masse m des fallenden Körpers spielt keine Rolle. Galileo Galilei zeigte, dass alle Körper gleich schnell fallen.
7. Im Vakuum fallen alle Körper gleich schnell, da dort keine Luftwiderstandskraft wirkt.
30px Merke
Der freie Fall ist eine Bewegung mit konstanter Beschleunigung (ohne Berücksichtigung des Luftwiderstandes). 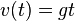 und und 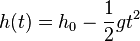 |
a) Nach dem 3. Newtonschen Gesetz sind F1 und F2 Kraft und Gegenkraft. Die beiden Kräfte sind gleich groß, aber entgegengesetzt gerichtet.
b) Die Beschleunigung, die der Ball erfährt ist 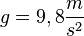 . Diese Beschleunigung ist überall auf der Erdoberfläche gleich.
. Diese Beschleunigung ist überall auf der Erdoberfläche gleich.
Die Erdbeschleunigung bewirkt, dass der Ball beim Fallen schneller wird.
b) Wegen 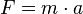 ist die Beschleunigung, die auf die Erde wirkt
ist die Beschleunigung, die auf die Erde wirkt 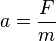 .
.
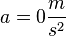 .
.
Die Bewegungsgleichung 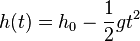 mit
mit 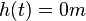 kann man nach t auflösen. Es ist
kann man nach t auflösen. Es ist 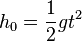 und
und 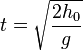 .
.
a) t = 1,01s
b) t = 1,43s
c) t = 2,02s
Mit diesen Zeiten kann man mit der Formel 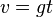 die Auftreffgeschwindigkeit berechnen.
die Auftreffgeschwindigkeit berechnen.
a) 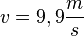
b) 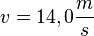
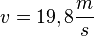
80/3 a) 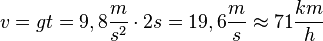
Die Durchschnittsgeschwindigkeit ist 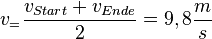 .
.
Die Fallhöhe ist wegen 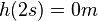 durch die Gleichung
durch die Gleichung 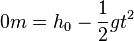 gegeben. Man erhält
gegeben. Man erhält 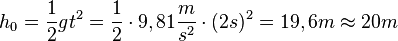
Die Aussage von Hans ist wohl übertrieben. Er spricht vielleicht von "gefühlten" 2s.
b) 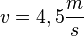 ergibt für
ergibt für 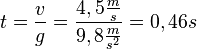
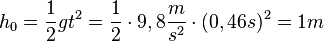
a) Für den freien Fall eines Körpers kennt man aus der Physik die Formel 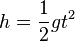 . Dabei ist g die Erdbeschleunigung
. Dabei ist g die Erdbeschleunigung 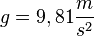 .
.
Setzt man die gemessene Zeit t = 3,44s in die Gleichung für h, dann erhält man 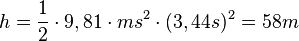 .
.
b) Sophie hat mit ihrem Einwand natürlich Recht. Die gemessene Zeit setzt sich zusammen aus der
- Fallzeit
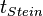 des Steins und
des Steins und
- der Zeit
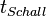 , die der Schall vom Boden bis zum Standort
, die der Schall vom Boden bis zum Standort
braucht. Es ist 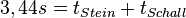 .
.
Der Stein und der Schall legen beide jeweils den Weg 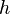 zurück. Dabei macht der Stein eine Bewegung mit konstanter Beschleunigung und der Schall eine Bewegung mit konstanter Geschwindigkeit.
zurück. Dabei macht der Stein eine Bewegung mit konstanter Beschleunigung und der Schall eine Bewegung mit konstanter Geschwindigkeit.
Der Stein wird mit konstanter Beschleunigung beschleunigt, dabei ist der zurückgelegte Weg 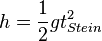 .
.
Der Schall macht eine Bewegung mit konstanter Geschwindigkeit, dabei ist der zurückgelegte Weg 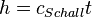 , wobei
, wobei 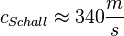 ist.
ist.
Da in beiden Fällen der gleiche Weg 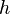 zurückgelegt wird, kann man die beiden Gleichungen gleich setzen.
zurückgelegt wird, kann man die beiden Gleichungen gleich setzen.
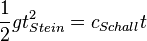
Dies ist eine Gleichung mit zwei Unbekannten 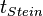 und
und 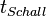 .
.
Von Sophia wissen wir, dass 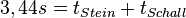 ist. Das ist die zweite Gleichung.
ist. Das ist die zweite Gleichung.
Man hat ein Gleichungssystem mit zwei Unbekannten:
(1) 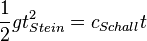
(2) 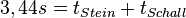
Löst man (2) nach 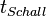 auf und setzt den erhaltenenen Term in (1) ein, dann hat man
auf und setzt den erhaltenenen Term in (1) ein, dann hat man
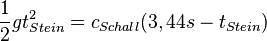
Man erhält eine quadratische Gleichung für 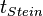 :
: 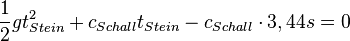
Mit der Lösungsformel erhält man 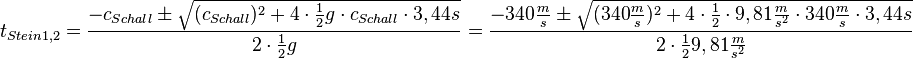
Das -Zeichen vor der Wurzel kann man weglassen, da sonst im Zähler etwas Negatives stehen würde und damit die Zeit negativ wäre. Dies kann nicht sein. Also kann man gleich nur mit dem + rechnen. Setzt man die Werte ein, dann erhält man <matsh>t_{Stein}=3,284s
und für den Schall 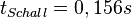 .
.
Damit erhält man für die Tiefe des Brunnens
- bei der Bewegung mit konstanter Beschleunigung des Steins
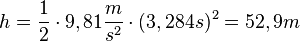
- bei der Bewegung des Schalls mit konstanter Geschwindigkeit
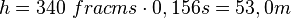 .
.
 , die auf die Erde wirkt und was bewirkt sie?
, die auf die Erde wirkt und was bewirkt sie?
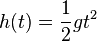 . Welchen Wert für die Tiefe des Brunnens erhält er?
. Welchen Wert für die Tiefe des Brunnens erhält er?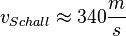 .
.

