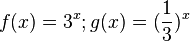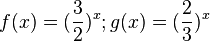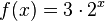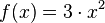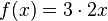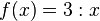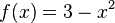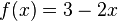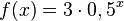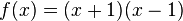M10 Eigenschaften der Exponentialfunktion: Unterschied zwischen den Versionen
(→Aufgaben) |
|||
| Zeile 83: | Zeile 83: | ||
=Aufgaben= | =Aufgaben= | ||
| − | {{Aufgaben-blau|5|2= | + | {{Aufgaben-blau|5|2=1. Zeichne die beiden Graphen G<sub>f</sub> und G<sub>g</sub> für das Intervall [-2;2]. Was stellst du fest? Erkläre deine Beobachtung!<br> |
| + | a) <math>f(x) = 3^x; g(x) = (\frac{1}{3})^x</math><br> | ||
| + | b) <math>f(x) = (\frac{3}{2})^x; g(x) = (\frac{2}{3})^x</math><br> | ||
| + | c) f(x) = 2,5<sup>x</sup>; g(x) = 0,4<sup>x</sup> | ||
| − | + | 2. Gib jeweils an, ob es sich um eine Exponentialfunktion, eine lineare Funktion, eine quadratische Funktion oder eine Bruchfunktion handelt. Zeichne jeweils den groben Verlauf des Graphen. <br> | |
| + | a) <math>f(x) = 3 \cdot 2^x</math><br> | ||
| + | b) <math>f(x) = 3 \cdot x^2</math><br> | ||
| + | c) <math>f(x) = 3 \cdot 2x</math><br> | ||
| + | d) <math>f(x) = 3 : x</math><br> | ||
| + | e) <math>f(x) = 3 - x^2</math><br> | ||
| + | f) <math>f(x) = 3 - 2x</math><br> | ||
| + | g) <math>f(x) = 3 \cdot 0,5^x</math><br> | ||
| + | h) <math>f(x) = (x + 1) (x-1)</math> }} | ||
| − | + | {{Lösung versteckt|1=1. siehe Applet 1 nach der Lösung.<br> | |
| + | Die Graphen sind achsensymmetrisch zur y-Achse. <br> | ||
| + | Begründung: Ersetzt man x durch -x, dann ist <math>f(-x) = a^{-x} = (\frac{1}{a})^x = g(x)</math> | ||
| + | |||
| + | |||
| + | 2.a) Exponentialfunktion <br> | ||
b) quadratische Funktion<br> | b) quadratische Funktion<br> | ||
c) lineare Funktion<br> | c) lineare Funktion<br> | ||
Version vom 20. November 2022, 10:52 Uhr
Inhaltsverzeichnis |
Die Funktion 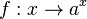
1. Für 0 < a < 1 ist die Exponentialfunktion streng monoton fallend, für a > 1 ist sie streng monoton steigend.
2. Für a = 1 ist die Funktion konstant.
3. Der Graph der Funktion verläuft für alle Werte von a oberhalb der x-Achse.
Die Funktion 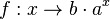
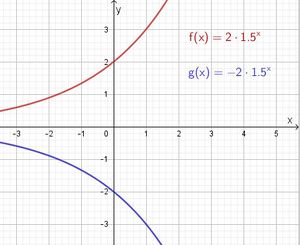
1. Wenn der Faktor b negativ ist, verläuft der Graph der Funktion unterhalb der x-Achse.
Zusammenfassung
95/4a Der Parameter a gibt das Wachstum an. Ist 0 < a < 1, so hat man eine exponentielle Abnahme, für 1 < a eine exponentielle Zunahme.
0 < a < 1: Je kleiner a ist, desto schwächer fällt der Graph. Nähert sich a dem Wert 1, dann fällt der Graph steiler.
1 < a: Je größer a wird, desto steiler wird der Graph.
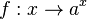 , wenn 0 < b < 1 wird er nach unten in y-Richtung gestaucht, wenn 1 < b ist nach oben in y-Richtung gestreckt. Wenn b negativ ist erfolgt eine Spiegelung an der x-Achse.
, wenn 0 < b < 1 wird er nach unten in y-Richtung gestaucht, wenn 1 < b ist nach oben in y-Richtung gestreckt. Wenn b negativ ist erfolgt eine Spiegelung an der x-Achse.Aufgaben
1. siehe Applet 1 nach der Lösung.
Die Graphen sind achsensymmetrisch zur y-Achse.
Begründung: Ersetzt man x durch -x, dann ist 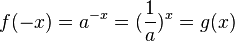
2.a) Exponentialfunktion
b) quadratische Funktion
c) lineare Funktion
d) Bruchfuntkion
e) quadratische Funktion
f) lineare Funktion
g) Exponentialfunktion
h) quadratische Funktion
Applet 1:
Applet 2:

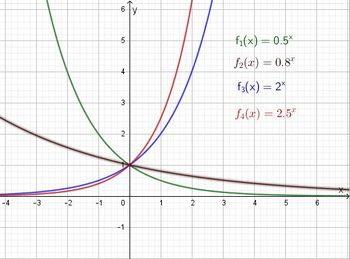
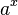 ist stets positiv.
ist stets positiv.
 mit
mit 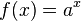 und
und  mit
mit 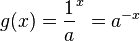 lliegen symmetrisch bezüglich der y-Achse.
lliegen symmetrisch bezüglich der y-Achse.
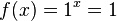 konstant,
konstant,