M11 Verschieben und Spiegeln der Exponentialkurven: Unterschied zwischen den Versionen

Aus RSG-Wiki
Wechseln zu: Navigation, Suche
Zeile 66: Zeile 66:
  
 
96/11 a)<math>3^{x+1}=3\cdot 3^x</math><br>
 
96/11 a)<math>3^{x+1}=3\cdot 3^x</math><br>
−
b)  
+
b) <math>10^{-x}=\left (\frac{1}{10}\right )^x</math><br>
−
}}
+
c) <math>2^{-x-1}=0,5\cdot\left (\frac{1}{2} \right )^x</math><br>
 +
d) <math>2^{-x} - 1=\left ( \frac{1}{2} \right )^x -1</math><br>
 +
e) <math>2^{2x+5}=32\cdot 4^x</math><br>
 +
f) <math>3^{-2x + 5}=243 \cdot \left ( \frac{1}{9} \right )^x</math><br>
 +
g) <math>3^{-2x} + 5=\left ( \frac{1}{9} \right )^x + 5</math><br>
 +
g) <math>4^{\frac{1}{2}x}=(\sqrt 4)^x  =2^x</math> }}

Version vom 26. Februar 2021, 14:10 Uhr

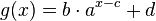Im folgenden Applet kann man mit den Schiebereglern für a, b, c und d die Werte der Parameter der Exponentialfunktion g mit g(x) = b \cdot a^{x-c} +d ändern.

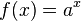Zur Kontrolle ist der Graph der Funktion f mit f(x) = a^x eingezeichnet.


Bleistift 35fach.jpg   Aufgabe 1

1. Verändere mit dem Schieberegler für c den Wert von c. Lass die anderen Schieberegler in ihrer Einstellung.
Was beobachtest du, wenn sich der Wert von c ändert? Notiere deine Beobachtungen.

2. Stelle den Schieberegler von c wieder auf c = 0. Verändere mit dem Schieberegler für d den Wert von d. Lass die anderen Schieberegler in ihrer Einstellung.
Was beobachtest du, wenn sich der Wert von d ändert? Notiere deine Beobachtungen.

3. Stelle den Schieberegler von d wieder auf d = 0. Verändere mit dem Schieberegler für bden Wert von b. Lass die anderen Schieberegler in ihrer Einstellung.
Was beobachtest du, wenn sich der Wert von c ändert? Notiere deine Beobachtungen.

1. Der Graph der Funktion 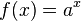f(x) = a^x wird um c in Richtung der x-Achse verschoben.
Ist c > 0, dann erfolgt die Verschiebung nach rechts, ist c < 0, dann erfolgt die Verschiebung nach links in x-Richtung.

2. Der Graph der Funktion 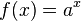f(x) = a^x wird um d in Richtung der y-Achse verschoben.
Ist d > 0, dann erfolgt die Verschiebung nach oben, ist d < 0, dann erfolgt die Verschiebung nach unten in y-Richtung.

3. Ist b > 1, wird der Graph von f in y-Richtung gestreckt.
Ist 0 < b < 1, wird der Graph von f in y-Richtung gestaucht.

Ist b < 0, erfolgt noch eine Spiegelung an der x-Achse.


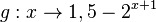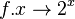Beispiel: Wie erhält man den Graphen der Funktion g:x\to 1,5 - 2^{x+1} aus dem Graphen der Funktion f.x \to 2^x?
1. Im Exponent steht x+1, also wird der Graph von f um -1 in x-Richtung (um 1 nach links) verschoben. Beachte, dass im Exponent x-c steht. Das bedeutet, dass x + 1 = x - (-1) zu betrachten ist und c = -1.
2. Vor der Potenz steht ein -, also wird der Graph von 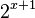2^{x+1} an der x-Achse gespiegelt.
3. Nun wird der Graph noch um d = 1,5 in y-Richtung (um 1,5 nach oben) verschoben.


Bleistift 35fach.jpg   Aufgabe 2

1. Verifiziere die drei Schritte im Applet.

2. Mache ähnliche Schritte für den Graph den Funktion g:x \to 3 - 4\cdot 2^x.

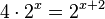Beachte 4\cdot 2^x =2^{x+2} !


Bleistift 35fach.jpg   Aufgabe 3

Buch S. 96 / 8


Bleistift 35fach.jpg   Aufgabe 4

Buch S. 96 / 9, 10, 11

96/9 A) 3x hat den Schnittpunkt (0;1) mit der y-Achse und ist monoton steigend, also Graph f.
B) 3x-1 hat den Schnittpunkt (0; 1/3) mit der y-Achse und ist monoton steigend, also Graph h.
C) -3x hat den Schnittpunkt (0;-1) mit der y-Achse, also Graph m<.
D) 3-x hat den Schnittpunkt (0;1) mit der y-Achse und ist monoton fallend, also Graph g.

96/10 a) Verschiebung um -3 in y-Richtung (3 nach unten).
Waagrechte Asymptote ist die positive Gerade y = -3.
b) Verschiebung um 4 in y-Richtung (4 nach oben).
Waagrechte Asymptote ist die positive Gerade y = 4.
c) Streckung um den Faktor 3 in y-Richtung.
Waagrechte Asymptote ist die positive x-Achse.
d) Stauchung um 1/3 in y-Richtung.
Waagrechte Asymptote ist die positive x-Achse.
e) Spiegelung an der x-Achse.
Waagrechte Asymptote ist die positive x-Achse.
f) Spiegelung an der x-Achse und verschieben um -3 in y-Richtung (3 nach unten).
Waagrechte Asymptote ist die positive Gerade y = -3.
g) Spiegelung an der x-Achse und Verschiebung um 1 in y-Richtung (1 nach oben).
Waagrechte Asymptote ist die positive Gerade y = 1. h) Spiegelung an der x-Achse und Streckung in y-Richtung um den Faktor 3.

96/11 a)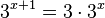3^{x+1}=3\cdot 3^x
b) 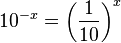10^{-x}=\left (\frac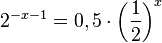{1}{10}\right )^x
c) 2^{-x-1}=0,5\cd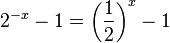ot\le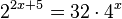f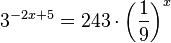t (\frac{1}{2} \rig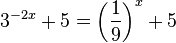ht )^x
d) 2^{-x} - 1=\left ( \frac{1}{2} \right )^x -1
e) 2^{2x+5}=32\cdot 4^x
f) 3^{-2x + 5}=243 \cdot \left ( \frac{1}{9} \right )^x
g) 3^{-2x} + 5=\left ( \frac{1}{9} \right )^x + 5

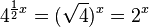
g) 4^{\frac{1}{2}x}=(\sqrt 4)^x =2^x
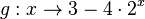Von „http://rsg.zum.de/index.php?title=M11_Verschieben_und_Spiegeln_der_Exponentialkurven&oldid=11447“