M10 Aufgaben zum Logarithmus: Unterschied zwischen den Versionen
| Zeile 25: | Zeile 25: | ||
b,c)<br> | b,c)<br> | ||
[[Datei:106-5.jpg]]<br> | [[Datei:106-5.jpg]]<br> | ||
| + | Man kann übrigens alle Zahlen auf der linken Seite, die man in der Aufgabe a) verwendet hat mit derselben Zehnerpotenzen multiplizieren. Die Skalierung bleibt. <br> | ||
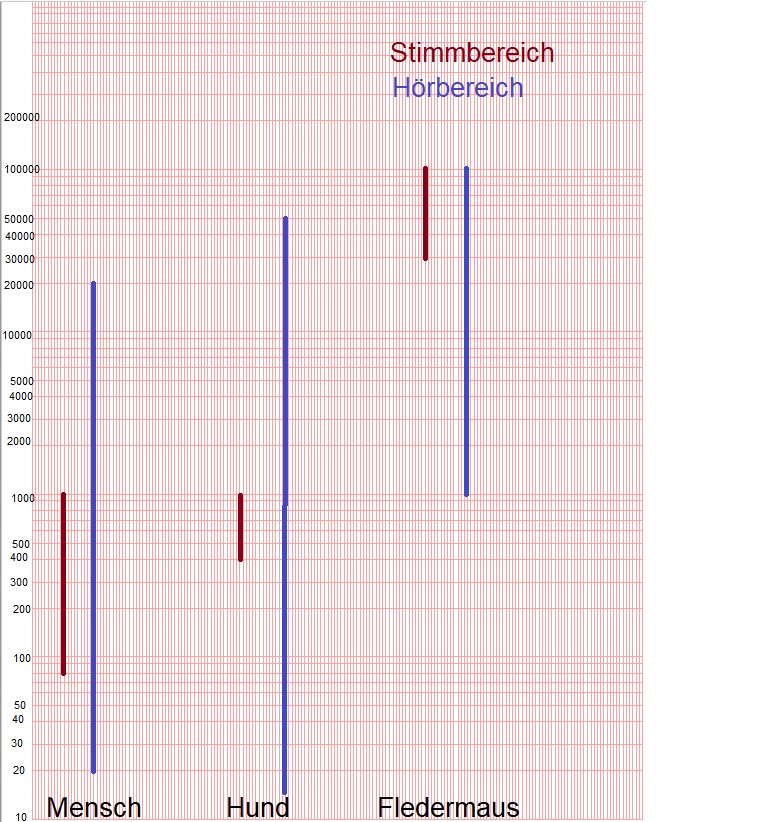
d) Da sich der Hörbereich des Hundes mit dem Stimmbereich der Fledermaus überschneidet, hört der Hund Schreie einer Fledermaus. }} | d) Da sich der Hörbereich des Hundes mit dem Stimmbereich der Fledermaus überschneidet, hört der Hund Schreie einer Fledermaus. }} | ||
{{Aufgaben-blau|4|2=Buch S. 107 / 6 (Richter-Skala)<br> | {{Aufgaben-blau|4|2=Buch S. 107 / 6 (Richter-Skala)<br> | ||
Buch S. 108 / 7 (Lautstärke) }} | Buch S. 108 / 7 (Lautstärke) }} | ||
Version vom 14. April 2021, 08:22 Uhr
Bei einem Logarithmuspapier sind eine oder beide Achsen mit einer logarithmischen Skala versehen.
Mehr zum Logarithmuspapier findest du auf dieser Seite bei Wikipedia
Sachverhalte, die durch ein logarithmisches oder Exponentialgesetz gegeben sind lassen sich als Geraden darstellen. In einem Diagramm kann man Geraden leichter identifizieren als die vorgegebene Funktion.
106/5
a) man unterteilt eine Strecke von 5cm in Teile und beschriftet sie mit 1, 2, 3, ..., 10. Die Teile erhält man, indem man den untersten (1-ten Strich bei 0cm ) mit 1 beschriftet und den obersten Strich (bei 5cm) mit 10 beschriftet. Die anderen Beschriftungen für x = 1, 2, 3, ... 9 erhält man indem man lg(x) berechnet, den Wert mit 5cm multipliziert und diesen Wert im Abstand von unten mit der Beschriftung x anträgt.
Das macht man dann für die nächsten 5cm genauso, nur, dass man nun für x die Zahlen 20, 30, 40, ... 100 nimmt, dann lg(x) bildet, mit 5cm multipliziert und diese Länge von der untersten Linie (bei 0cm) aus anträgt. ...
b,c)
Man kann übrigens alle Zahlen auf der linken Seite, die man in der Aufgabe a) verwendet hat mit derselben Zehnerpotenzen multiplizieren. Die Skalierung bleibt.

