M11 Aufgaben zu Logarithmus- und Exponentialfunktionen: Unterschied zwischen den Versionen
| Zeile 14: | Zeile 14: | ||
{{Lösung versteckt|1=Es ist P(0;1), Q(2;e<sup>2</sup>), f'(x) = e<sup>x</sup> imd f'(0) = 1 und f'(2) = e<sup>2</sup>. <br> | {{Lösung versteckt|1=Es ist P(0;1), Q(2;e<sup>2</sup>), f'(x) = e<sup>x</sup> imd f'(0) = 1 und f'(2) = e<sup>2</sup>. <br> | ||
Gleichung der Tangente t<sub>1</sub> in P: y = x + 1<br> | Gleichung der Tangente t<sub>1</sub> in P: y = x + 1<br> | ||
| − | Gleichung der Tangente t<sub>2</sub> in Q: y = e<sup>2</sup>·x - e<sup>2</sup> | + | Gleichung der Tangente t<sub>2</sub> in Q: y = e<sup>2</sup>·x - e<sup>2</sup>. (t erhält man aus der Gleichung e<sup>2</sup> = e<sup>2</sup>·2 - t.)<br> |
| − | (t erhält man aus der Gleichung e<sup>2</sup> = e<sup>2</sup>·2 - t.)<br> | + | |
Den Schnittwinkel der beiden Tangenten erhält man, indem man <math>\varphi = \varphi_2 - \varphi_1</math> bildet, wenn <math>\varphi_1</math> der Schnittwinkel von t<sub>1</sub> mit der Waagrechten im Schnittpunkt und <math>\varphi_2</math> der Schnittwinkel von t<sub>2</sub> mit der Waagrechten im Schnittpunkt ist.<br> | Den Schnittwinkel der beiden Tangenten erhält man, indem man <math>\varphi = \varphi_2 - \varphi_1</math> bildet, wenn <math>\varphi_1</math> der Schnittwinkel von t<sub>1</sub> mit der Waagrechten im Schnittpunkt und <math>\varphi_2</math> der Schnittwinkel von t<sub>2</sub> mit der Waagrechten im Schnittpunkt ist.<br> | ||
| − | Es ist <math>tan(\varphi_1) = 1</math>, also ist <math>\varphi_1 = 45^o<math>. <br> | + | Es ist <math>tan(\varphi_1) = 1</math>, also ist <math>\varphi_1 = 45^o</math>. <br> |
Es ist <math>tan(\varphi_2) = e^2</math>, also ist <math>\varphi_2=82,3^o</math><br> | Es ist <math>tan(\varphi_2) = e^2</math>, also ist <math>\varphi_2=82,3^o</math><br> | ||
Damit ist <math>\varphi = \varphi_2 - \varphi_1 = 82,3^o - 45^o = 37,3^o</math>.<br> | Damit ist <math>\varphi = \varphi_2 - \varphi_1 = 82,3^o - 45^o = 37,3^o</math>.<br> | ||
| Zeile 38: | Zeile 37: | ||
<math>x = -\frac{2}{3}(1-ln(2))\approx -0,2</math> | <math>x = -\frac{2}{3}(1-ln(2))\approx -0,2</math> | ||
| − | <math>y = f(-\frac{2}{3}(1-ln(2 | + | <math>y = f(-\frac{2}{3}(1-ln(2)) \approx 1,11</math>, also S(-0,2; 1,11) (näherungsweise, aber genügend genau!) |
Den Schnittwinkel zwischen beiden Graphen erhält man, indem man den Schnittwinkel der Tangenten in S an G<sub>f</sub> und G<sub>g</sub> bestimmt. Dazu muss man nicht die Tangetengleichungen aufstellen. Es reicht, wenn man die Steigungen in S kennt, denn es ist <math>tan(\varphi) = f'(x_S)</math>.<br> | Den Schnittwinkel zwischen beiden Graphen erhält man, indem man den Schnittwinkel der Tangenten in S an G<sub>f</sub> und G<sub>g</sub> bestimmt. Dazu muss man nicht die Tangetengleichungen aufstellen. Es reicht, wenn man die Steigungen in S kennt, denn es ist <math>tan(\varphi) = f'(x_S)</math>.<br> | ||
| Zeile 54: | Zeile 53: | ||
A(0;1) [[Datei:152-8b 1.jpg|350px]] | A(0;1) [[Datei:152-8b 1.jpg|350px]] | ||
| − | Die Tangente in B soll senkrecht zu einer Geraden k mit Steigung -2 sein. Die Tangente in B an G<sub>g</sub> hat dann die Steigung 0,5. Also ist g'(x<sub>B</sub>) = 0,5.<br> | + | Die Tangente in B soll senkrecht zu einer Geraden k mit Steigung -2 sein. Die Tangente in B an G<sub>g</sub> hat dann die Steigung 0,5. Also ist g'(x<sub>B</sub>) = 0,5.<br<sup>> |
| − | <math>0,5=\frac{1}{2}e^{x+1} \qquad |\cdot 2</math> | + | <math>0,5=\frac{1}{2}e^{x+1} \qquad |\cdot 2</math</sup>> |
<math>1=e^{x+1} \qquad |logarithmieren</math> | <math>1=e^{x+1} \qquad |logarithmieren</math> | ||
<math> 0 = x+1</math> ergibt <math> x = -1</math> <br> | <math> 0 = x+1</math> ergibt <math> x = -1</math> <br> | ||
B(-1;0,5) [[Datei:152-8b 2.jpg|350px]] }} | B(-1;0,5) [[Datei:152-8b 2.jpg|350px]] }} | ||
| + | |||
| + | Buch S. 153 / 4 | ||
| + | |||
| + | {{Lösung versteckt|1=Graph 1 gehört zu Funktion f (f ist die einzige Funktion mit D = R<sup>+</sup>.)<br> | ||
| + | Graph 2 gehört zu Funktion d (d hat bei x = 0 eine Polstelle.)<br> | ||
| + | Graph 3 gehört zu Funktion a (e<sup>x</sup> wird um den Faktor 2 in y-Richtung gestreckt, ebenso in x-Richtung, also ist der Verlauf wie bei "e-Funktion" durch (0;2).)<br> | ||
| + | Graph 4 gehört zu Funktion b (-e<sup>x</sup> ist e<sup>x</sup> an der x-Achse gespiegelt und wird um 3 nach oben verschoben.)<br> | ||
| + | Graph 5 gehört zu Funktion c (c ist die einzig verbleibende Funktion mit c(0) = 2.)<br> | ||
| + | Graph 6 gehört zu Funktion e (e hat als einzige Funktion eine Nullstelle bei x = 1.) }} | ||
Version vom 15. April 2021, 17:49 Uhr
Buch S. 151 / 4
151 / 4 Da man nur eine Stammfunktion angeben soll, wird auf + C verzichtet.
a) F(x) = ex + x
b) F(x) = - e-x
c) F(x) = 0,5(ex - e-x)
d) F(x) = 0,5x2 + 2x + ex+2
e) F(x) = e1+x
f) F(x) = 2e0,5x
Buch S. 152 / 7a
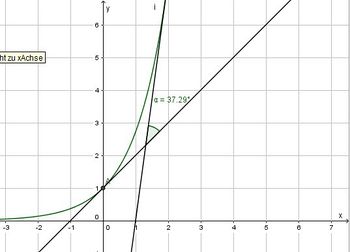
Es ist P(0;1), Q(2;e2), f'(x) = ex imd f'(0) = 1 und f'(2) = e2.
Gleichung der Tangente t1 in P: y = x + 1
Gleichung der Tangente t2 in Q: y = e2·x - e2. (t erhält man aus der Gleichung e2 = e2·2 - t.)
Den Schnittwinkel der beiden Tangenten erhält man, indem man 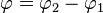 bildet, wenn
bildet, wenn 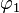 der Schnittwinkel von t1 mit der Waagrechten im Schnittpunkt und
der Schnittwinkel von t1 mit der Waagrechten im Schnittpunkt und 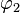 der Schnittwinkel von t2 mit der Waagrechten im Schnittpunkt ist.
der Schnittwinkel von t2 mit der Waagrechten im Schnittpunkt ist.
Es ist 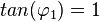 , also ist
, also ist 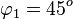 .
.
Es ist 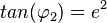 , also ist
, also ist 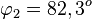
Damit ist 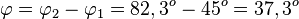 .
.
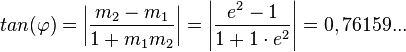 ergibt
ergibt 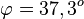 .
.Buch S. 152 / 8
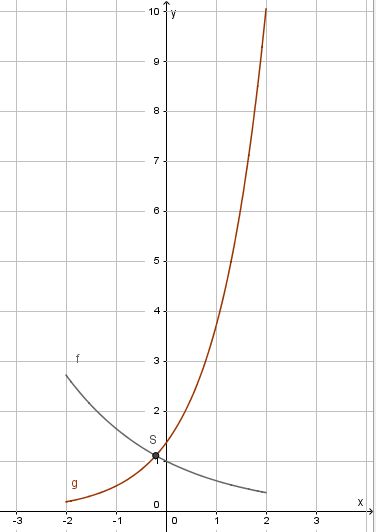
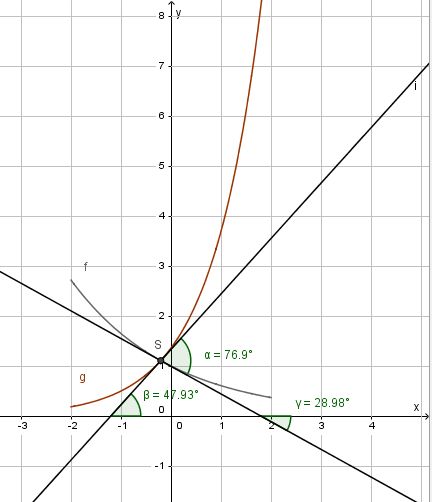
a) Die Koordinaten des Schnittpunkts S der beiden Graphen erhält man, indem man die Funktionsterme gleich setzt.
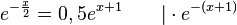
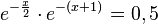
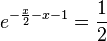
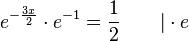
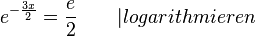
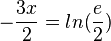
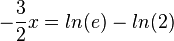
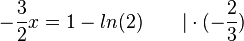
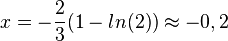
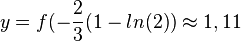 , also S(-0,2; 1,11) (näherungsweise, aber genügend genau!)
, also S(-0,2; 1,11) (näherungsweise, aber genügend genau!)
Den Schnittwinkel zwischen beiden Graphen erhält man, indem man den Schnittwinkel der Tangenten in S an Gf und Gg bestimmt. Dazu muss man nicht die Tangetengleichungen aufstellen. Es reicht, wenn man die Steigungen in S kennt, denn es ist 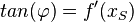 .
.
Man berechnet 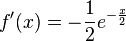 und
und 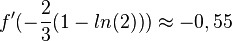 .
.
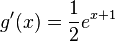 und
und 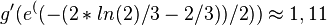 .
.
Für  ist
ist 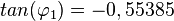 und
und 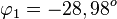 und
und
für  ist
ist 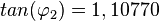 und
und 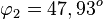 .
.
Damit ist 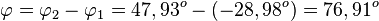 .
.
b) Die Tangente in A soll parallel zu einer Geraden h mit Steigung - 0,5 sein. Also ist f'(xA) = - 0,5.
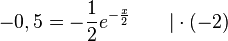
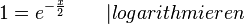
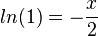 ergibt
ergibt 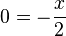 und
und 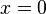 .
.
A(0;1) 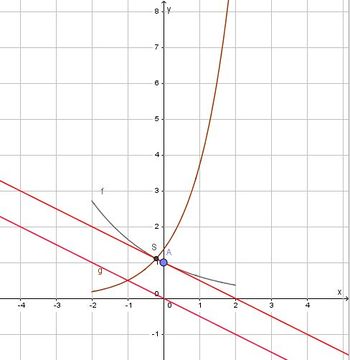
Die Tangente in B soll senkrecht zu einer Geraden k mit Steigung -2 sein. Die Tangente in B an Gg hat dann die Steigung 0,5. Also ist g'(xB) = 0,5.<br>
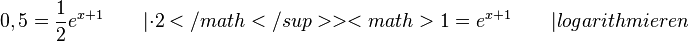
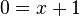 ergibt
ergibt 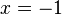
B(-1;0,5) 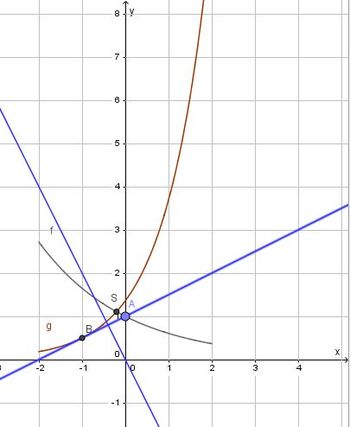 </div>
</div>
Buch S. 153 / 4
Graph 1 gehört zu Funktion f (f ist die einzige Funktion mit D = R+.)
Graph 2 gehört zu Funktion d (d hat bei x = 0 eine Polstelle.)
Graph 3 gehört zu Funktion a (ex wird um den Faktor 2 in y-Richtung gestreckt, ebenso in x-Richtung, also ist der Verlauf wie bei "e-Funktion" durch (0;2).)
Graph 4 gehört zu Funktion b (-ex ist ex an der x-Achse gespiegelt und wird um 3 nach oben verschoben.)
Graph 5 gehört zu Funktion c (c ist die einzig verbleibende Funktion mit c(0) = 2.)

