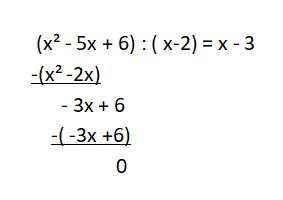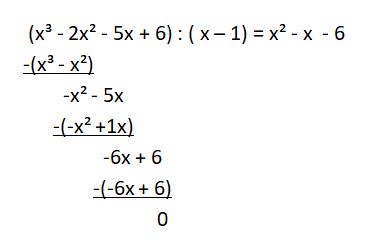M10 Nullstellen von Polynomfunktionen: Unterschied zwischen den Versionen
| Zeile 67: | Zeile 67: | ||
a) f(x) = x<sup>3</sup> - 2x<sup>2</sup> - 4x + 8<br> | a) f(x) = x<sup>3</sup> - 2x<sup>2</sup> - 4x + 8<br> | ||
b) f(x) = 3x<sup>3</sup> - 10x<sup>2</sup> + 7x - 12<br> | b) f(x) = 3x<sup>3</sup> - 10x<sup>2</sup> + 7x - 12<br> | ||
| − | c) f(x) = x<sup>4</sup> + 2x< | + | c) f(x) = x<sup>4</sup> + 2x<sup>3</sup> - 4x<sup>2</sup> - 10x - 5<br> |
}} | }} | ||
Aktuelle Version vom 23. Juli 2021, 12:51 Uhr
Für quadratische Funktionen hat man mit der Lösungsformel ein probates Mittel Nullstellen der Funktion zu bestimmen.
a) Es ist x2 - 5x + 6 = (x-2)(x-3), also sind die Nullstelle x1 = 2, x2 = 3.
b) 3x2 - 5x -2 = 0 hat die Lösungen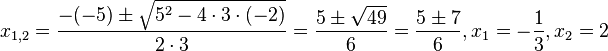 
Für Polynomfunktionen höheren Grades gibt es keine Lösungsformel. Wenn man Nullstellen "erraten" kann, dann hat man mit Hilfe der Polynomdivision die Möglichkeit den Grad des Polynoms, das weiter zu untersuchen ist, zu vermindern.
Bevor wir die Polynomodivision kennenlernen, wollen wir die Division bei Zahlen betrachten. Dazu betrachten wir den Quotienten 736 : 32.
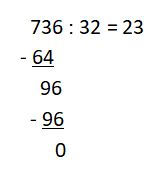
1. Zuerst schaut man wie oft 32 in 73 geht, dazu dividiert man 73 : 32 und erhält, das 32 zweimal in 73 erhalten ist. Man hat dividiert.
2. Nun multipliziert man 32 mit 2 und erhält 64. Man hat multipliziert.
3. 64 zieht man von 73 ab und schreibt als Ergebnis 9. Man hat subtrahiert.
4. Nun holt man 6 herunter und macht das gleiche Verfahren (1. - 3.) für 96 und 32.
...
Man hat für die Division bei Zahlen ein Schema aus dividieren - multiplizieren - subtrahieren.
Dieses Schema lässt sich auf die Division von Polynomen übertragen. Die Zahl 736 ist eine Dezimalsystem und lässt sich schreiben mit den Stufenzahlen 7·102 + 3·10 + 6. Ersetzt man 10 durch x, dann entspricht der Zahl 736 das Polynom 7x2 + 3x + 6.
32 entspricht dann dem Polynom 3x + 2 und die Division 736 : 32 entspricht der Division (7x2 + 3x + 6) : (3x + 2) der Terme (7x2 + 3x + 6) und (3x + 2).
Da die Terme Polynome sind spricht man von der Polynomdivision.
Um eine Polynomdivision durchzuführen, benötigt man den Term und eine Nullstelle dieses Terms. Wenn man die Nullstelle nicht sieht, so kann man die Zahlen 1, 2, 3, 0, -1, -2, -3 ausprobieren.
Beim Polynom x2 - 5x + 6 findet man durch Probieren die Nullstelle 2. Damit hat man die Polynomdivision (x2 - 5x + 6) : (x - 2).
Mit dem Schema dividieren - multiplizieren - subtrahieren geht man hier folgendermaßen vor:
1. Man dividiert x² durch x und erhält x² : x = x (dividieren)
2. Man multipliziert den Divisor x - 2 mit x, also x² - 2x. (multiplizieren).
3. Man subtrahiert x² - 2x von x² - 5x und erhält -3x (subtrahieren).
4. Nun holt man zu den -3x die Zahl 6 herunter und hat -3x + 6.
5. Nun dividiert man -3x durch x und erhält -3 (dividieren).
6. Nun multipliziert den Divisor x - 2 mit -3 und erhält -3x + 6 (multiplizieren).
7. Nun subtrahiert man -3x + 6 von -3x + 6 und erhält 0 (subtrahieren).
Zur Sicherheit kann man die Probe machen: (x - 2)(x - 3) = x2 - 5x + 6
Dies führt dann dazu, dass das quadratische Polynom x2 - 5x + 6 die zwei Nullstellen x1 = 2 und x2 = 3 hat.
Bei Polynomen vom Grad 2 hat man ja mit der Lösungsformel eine Möglichkeit die Nullstellen (oder auch keine) zu finden. Für Polynome vom Grad größer als 2 gibt es keine Lösungsformel. Wie schaut es nun bei einem Polynom vom Grad 3 aus?
Für das Polynom 3. Grades x3 - 2x2 - 5x + 6 findet man durch Probieren als Nullstelle x = 1.
Die weiteren Nullstellen des Polynoms x² - x - 6 erhält man etwa mit der Lösungsformel zu x2 = -2 und x3 = 3.
Weitere Beispiele:
a) Durch Provieren findet man x1 = 2 als Nullstelle.
(x3 - 2x2 - 4x + 8) : (x - 2) = x2 - 4
Das Polynom x2 - 4 hat die zwei Nullstellen x2 = -2 und x3 = 2.
f hat also zwei Nullstellen x = 2 als zweifache Nullstelle und x = -2 als einfache Nullstelle.
Der Term der Polynomfuntkion lässt sich schreiben x3 - 2x2 - 4x + 8 = (x - 2)2 (x+2)
b) Man findet durch Probieren die Nullstelle x = 3.
(3x3 - 10x2 + 7x - 12) : (x - 3) = 3x2 - x + 4
Die quadratische Gleichung 3x2 - x + 4 = 0 hat die Diskriminante D = 1 - 4·3·4 = -47 und f hat damit keine weiteren Nullstellen.
f hats also nur eine Nullstelle, nämlich x = 3.
c) Durch Probieren findet man die Nullstelle x1 = -1.
(x4 + 2x3 - 4x2 - 10x - 5) : (x-1) = x3 + x2 - 5x - 5
Durch Probieren findet man für das Polynom 3. Grades x3 + x2 - 5x - 5 die Nullstelle x = -1.
x = -1 ist also eine zweifache Nullstelle von f(x).
(x3 + x2 - 5x - 5) : (x + 1) = x2 - 5
Die Gleichung x2 - 5 = 0 hat die Lösungen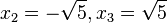 
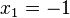als zweifache Nullstelle und .
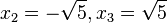