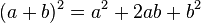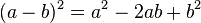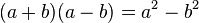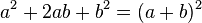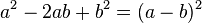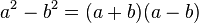Version vom 6. März 2023, 10:01 Uhr

Die binomischen Formeln erleichtern einem Termumformungen, sowohl von Summe in Produkt, als auch umgekehrt Produkt in Summe. Eigentlich braucht man sie nicht unbedingt. Wer sich mit dem Rechnen rund um Klammern gut auskennt kommt leicht ohne sie aus. Für alle anderen erleichtern die binomischen Formeln das Umformen und damit das Leben. Sie stellen eine Abkürzung da und wer geht nicht gerne einen leichteren Weg. Man muss sie allerdings einmal lernen.

Inhaltsverzeichnis

1 Die binomischen Formeln
2 Veranschaulichung der binomischen Formeln
3 Beispiele
4 Umgekehrt: Mache aus einer Summe/Differenz ein Produkt
- 4.1 Klapptests
- 4.2 Und wer noch nicht genug hat: Weitere Aufgaben mit Lösungen

Die binomischen Formeln

Merke

Die drei binomische Formeln lauten:

1. binomische Formel: $(a + b)^2 = a^2 + 2ab+b^2$

2. binomische Formel: $(a - b)^2 = a^2 - 2ab +b^2$

3. binomische Formel: $(a + b ) (a - b) = a^2 - b^2$

Alle drei binomischen Formeln lassen sich durch Termumformung leicht herleiten:

1. binomische Formel: 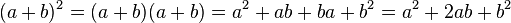$(a+b)^2 = (a+b)(a+b)=a^2+ab+ba+b^2=a^2+2ab+b^2$

2. binomische Formel: 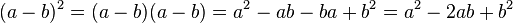$(a-b)^2 = (a-b)(a-b)=a^2-ab-ba+b^2=a^2-2ab+b^2$

3. binomische Formel: 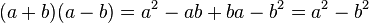$(a+b)(a-b) = a^2-ab+ba-b^2=a^2-b^2$

Für das Zahlenrechnen gelten sie natürlich auch, sind aber eher uninteressant. Es ist 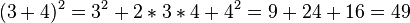$(3+4)^2=3^2+2*3*4+4^2=9+24+16=49$ was sich natürlich leichter durch 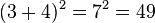$(3+4)^2=7^2=49$ berechnet.

Kommen Buchstaben vor, dann erleichtern die binomischen Formeln das Leben!

Veranschaulichung der binomischen Formeln

1. Binomische Formel: (a + b)² = a² + 2ab + b² : Plusformel

2. Binomische Formel: (a - b)² = a² - 2ab + b² : Minusformel

3. Binomische Formel: (a + b) (a - b) = a² - b² : Plusminusformel

Beispiele

Tipp: Schaut in die binomische Formel und macht euch klar, was a und b ist. Und dann setzt ihr für a und b die Zahlen oder Buchstaben ein. Vergleicht die Formel mit dem was oben steht, dann sollte es klar sein!

1. binomischen Formel

Zuerst verwandeln wir ein Quadrat in eine Summe.
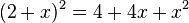
$(2+x)^2 = 4 + 4x +x^2$
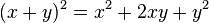
$(x+y)^2 = x^2 + 2xy+y^2$
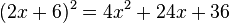
$(2x + 6)^2=4x^2+24x+36$
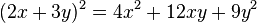
$(2x + 3y)^2=4x^2+12xy+9y^2$
Natürlich geht es auch umgekehrt.
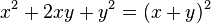
$x^2 + 2xy + y^2= (x+y)^2$
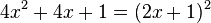
$4x^2 + 4x + 1= (2x+1)^2$
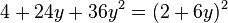
$4 +24y+36y^2=(2+6y)^2$
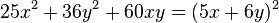$25x^2+36y^2+60xy=(5x+6y)^2$ Zuerst den Term in die richtige Reihenfolge bringen!

2. binomischen Formel

Zuerst verwandeln wir wieder ein Quadrat in eine Summe.
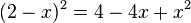
$(2-x)^2 = 4 - 4x +x^2$
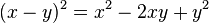
$(x-y)^2 = x^2 - 2xy+y^2$
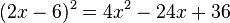
$(2x - 6)^2=4x^2-24x+36$
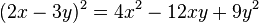
$(2x - 3y)^2=4x^2-12xy+9y^2$
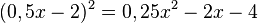
$(0,5x - 2)^2=0,25x^2-2x-4$
Und nun verwandeln wir eine Summe in ein Quadrat.
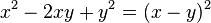
$x^2 - 2xy + y^2= (x-y)^2$
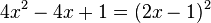
$4x^2 - 4x + 1= (2x-1)^2$
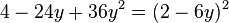
$4 -24y+36y^2=(2-6y)^2$
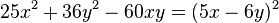$25x^2+36y^2-60xy=(5x-6y)^2$ Auch hier wieder zuerst den Term in die richtige Reihenfolge bringen!
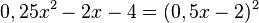
$0,25x^2-2x-4=(0,5x - 2)^2$

3. binomischen Formel

Zuerst verwandeln wir ein Produkt in eine Differenz.
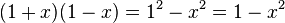
$(1+x)(1-x)=1^2-x^2=1-x^2$
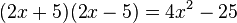
$(2x+5)(2x-5)=4x^2-25$
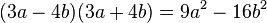
$(3a-4b)(3a+4b)=9a^2-16b^2$
Eine Differenz aus Quadraten lässt sich einfach in ein Produkt verwandeln:
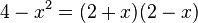
$4-x^2=(2+x)(2-x)$
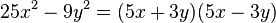
$25x^2-9y^2=(5x+3y)(5x-3y)$
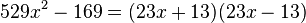
$529x^2 - 169=(23x+13)(23x-13)$
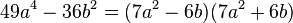
$49a^4-36b^2=(7a^2-6b)(7a^2+6b)$

Umgekehrt: Mache aus einer Summe/Differenz ein Produkt

Die binomischen Formeln sind Gleichungen, die man nicht nur von links nach rechts lesen kann, sondern auch von rechts nach links. Man kann also eine passende Summe oder Differenz in ein Produkt umwandeln, was manchmal sehr hilfreich ist - etwa beim Kürzen von Brüchen.

Merke

Die drei binomische Formeln lauten:

1. binomische Formel: $a^2 + 2ab+b^2 = (a + b)^2$

2. binomische Formel: $a^2 - 2ab +b^2 = (a - b)^2$

3. binomische Formel: $a^2 - b^2 = (a + b ) (a - b)$

Aufgaben
Einfache Übung zum Erkennen von binomischen Termen]
Faktorisieren von binomischen Termen
Faktorisieren von binomischen Termen
Faktorisieren von binomischen Termen - etwas schwerer
Faktorisieren von binomischen Termen - noch etwas schwerer

Multiple Choice Test zu binomischen Termen

Das Faktorisieren wird hier nochmals ausführlich erklärt.
Eine häufige Fehlerquelle ist das mittlere Glied.
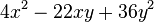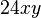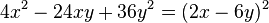$4x^2-22xy+36y^2$ lässt sich durch eine binomische Formel nicht in ein Produkt umwandeln! Das gemische Glied müsste $24xy$ lauten, denn es ist $4x^2-24xy+36y^2=(2x-6y)^2$ .

Klapptests

1. und 2. binomische Formel - Ausmultiplizieren: Test 1, Test 2, Test 3, [1]
1. und 2. biomische Formel - Faktorisieren: Test 1, Test 2, Test 3, Test 4
3. binomische Formel: Test 1 Verwandle den Term auf der linken Seite mit der 3. binomischen Formel in ein Produkt.

@@ Zeile 112: / Zeile 112: @@
 *http://www.brinkmann-du.de/mathe/aufgabenportal/p0_binform_01/p0_binform_01.htm
-*http://www.strobl-f.de/ueb710.pdf mit Lösungen: http://www.strobl-f.de/lsg710.pdf
+*http://www.strobl-f.de/ueb73.pdf mit Lösungen: http://www.strobl-f.de/lsg73.pdf
 *http://www.realmath.de/Mathematik/Mathepage/binomei.html
 *http://www.frustfrei-lernen.de/mathematik/binomische-formeln-aufgaben-uebungen-mathematik.html
 *http://www.abfrager.de/gymnasium/klasse8/mathematik/binomischeformeln.htm
 *http://www.zum.de/dwu/depothp/hp-math/hpmbf01.htm (Zuordnungstest)

Binomische Formeln: Unterschied zwischen den Versionen

Version vom 6. März 2023, 10:01 Uhr

Inhaltsverzeichnis

Die binomischen Formeln

Veranschaulichung der binomischen Formeln

Beispiele

1. binomischen Formel

2. binomischen Formel

3. binomischen Formel

Umgekehrt: Mache aus einer Summe/Differenz ein Produkt

Klapptests

Und wer noch nicht genug hat: Weitere Aufgaben mit Lösungen

Navigationsmenü

Meine Werkzeuge

Namensräume

Varianten

Ansichten

Aktionen

Suche

Navigation

Fächer

Hilfen

Werkzeuge