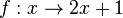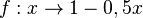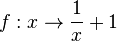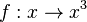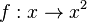Umkehrfunktion Beispiele: Unterschied zwischen den Versionen
Aus RSG-Wiki
| Zeile 1: | Zeile 1: | ||
| − | {{Aufgabe|Bestimme die Umkehrfunktion graphisch und | + | Um das bisher behandelte zu üben beginnen wir mit ähnlichen Beispielen, also linearen Funktionen |
| + | |||
| + | {{Aufgabe|Bestimme die Umkehrfunktion graphisch und algebraisch der Funktion | ||
# <math>f: x \rightarrow 2x + 1</math> | # <math>f: x \rightarrow 2x + 1</math> | ||
# <math>f: x \rightarrow 1 -0,5x</math> | # <math>f: x \rightarrow 1 -0,5x</math> | ||
| − | + | }} | |
| − | + | ||
| − | + | {{Lösung versteckt| | |
| + | |||
| + | }} | ||
| + | |||
| + | Nun wollen wir auch andere Funktionstypen untersuchen: | ||
| + | |||
| + | {{Aufgabe|Bestimme die Umkehrfunktion graphisch und algebraisch der Funktion | ||
| + | <math>f: x \rightarrow \frac{1}{x}+1</math> | ||
| + | }} | ||
| + | |||
| + | {{Lösung versteckt| | ||
| + | |||
| + | }} | ||
| + | |||
| + | {{Aufgabe|Bestimme die Umkehrfunktion durch Wertetabelle, graphisch und algebraisch der Funktion | ||
| + | <math>f: x \rightarrow x^3</math> | ||
| + | }} | ||
| + | |||
| + | {{Lösung versteckt| | ||
| + | |||
| + | }} | ||
| + | |||
| + | {{Aufgabe|Bestimme die Umkehrfunktion graphisch und algebraisch der Funktion | ||
| + | <math>f: x \rightarrow x^2</math> | ||
}} | }} | ||
Version vom 22. Mai 2012, 20:49 Uhr
Um das bisher behandelte zu üben beginnen wir mit ähnlichen Beispielen, also linearen Funktionen
30px Aufgabe
Bestimme die Umkehrfunktion graphisch und algebraisch der Funktion |
Nun wollen wir auch andere Funktionstypen untersuchen:
30px Aufgabe
Bestimme die Umkehrfunktion graphisch und algebraisch der Funktion
|
30px Aufgabe
Bestimme die Umkehrfunktion durch Wertetabelle, graphisch und algebraisch der Funktion
|
30px Aufgabe
Bestimme die Umkehrfunktion graphisch und algebraisch der Funktion
|