Einfluss von Parametern auf den Funktionsgraph: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
| − | Oft ist es notwendig Parameter im Funktionsterm zu haben, um die Lösung für ein Problem zu finden. Was verändern Parameter <math> a, b, c, d \in \mathbb R</math>, wenn man sie im Funktionsterm <math>g(x) = a f(b(x-c))+d</math> variiert? | + | Oft ist es notwendig Parameter im Funktionsterm zu haben, um die Lösung für ein Problem zu finden. Was verändern Parameter <math> a, b, c, d \in \mathbb R</math> die Funktion bzw. ihren Graphen, wenn man sie im Funktionsterm <math>g(x) = a f(b(x-c))+d</math> variiert? |
Verändere dazu im Applet mit den Schiebereglern die Werte von <math>a, b, c, d</math> und beobachte die Auswirkungen auf den Graphen von <math>g</math>. | Verändere dazu im Applet mit den Schiebereglern die Werte von <math>a, b, c, d</math> und beobachte die Auswirkungen auf den Graphen von <math>g</math>. | ||
Aktuelle Version vom 12. Juli 2014, 06:58 Uhr
Oft ist es notwendig Parameter im Funktionsterm zu haben, um die Lösung für ein Problem zu finden. Was verändern Parameter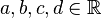 
die Funktion bzw. ihren Graphen, wenn man sie im Funktionsterm 
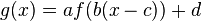variiert?
Verändere dazu im Applet mit den Schiebereglern die Werte von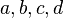 
und beobachte die Auswirkungen auf den Graphen von 
.
- Verschiebung der Funktionsgraphen
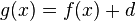
Der Parameter d bewirkt ein Verschieben des Graphen der Funktion f um |d| in Richtung der y-Achse und zwar für d > 0 nach oben und für d < 0 nach unten.
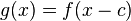
Der Parameter c bewirkt ein Verschieben des Graphen der Funktions f um |c| in Richtung der x-Achse und zwar für c > 0 nach rechts und für c < 0 nach links.
- Strecken und Stauchen des Funktionsgraphen
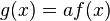
Der Parameter a bewirkt ein Strecken bzw. Stauchen des Graphen der Funktion f in Richtung der y-Achse und zwar für a > 1 ein Strecken bzw. für 0 < a < 1 ein Stauchen.
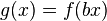
Der Parameter b bewirkt ein Strecken bzw. Stauchen des Graphen der Funktion f in Richtung der x-Achse mit dem Faktor 
und zwar für 0 < b < 1 ein Strecken bzw. für b > 1 ein Stauchen.
- Spiegeln des Funktionsgraphen
Für a = -1 wird der Graph der Funktion f an der x-Achse gespiegelt.
Für b = -1 wird der Graph der Funktion f an der y-Achse gespiegelt.
Für a = -1 und b = -1 wird der Graph der Funktion f am Ursprung gespiegelt.
