1m13 2014-15: Unterschied zwischen den Versionen
(→Die Ableitungsfunktion) |
(→Die Ableitungsfunktion) |
||
| Zeile 41: | Zeile 41: | ||
Gegeben ist die Polynomfunktion <math> f: x \rightarrow \frac{1}{24}(x^4-16x^2)</math>.<math>A(x,y)</math> ist ein Punkt auf dem Graphen von <math>f</math>. In <math>A</math> ist die Tangente an den Graphen von <math>f</math>, diese hat die Steigung <math>m</math>. Trägt man über jeden x-Wert von <math>A</math> den Steigungswert <math>m</math> an, so erhält man den Punkt <math>M(x,m)</math>. Bewegt man nun den Punkt <math>A</math> auf dem Graphen von <math>f</math> so variiert auch der Punkt <math>M</math> und die Spur des Punktes <math>M</math> gibt den Graphen der Ableitungsfunktion <math>f'</math> wieder. | Gegeben ist die Polynomfunktion <math> f: x \rightarrow \frac{1}{24}(x^4-16x^2)</math>.<math>A(x,y)</math> ist ein Punkt auf dem Graphen von <math>f</math>. In <math>A</math> ist die Tangente an den Graphen von <math>f</math>, diese hat die Steigung <math>m</math>. Trägt man über jeden x-Wert von <math>A</math> den Steigungswert <math>m</math> an, so erhält man den Punkt <math>M(x,m)</math>. Bewegt man nun den Punkt <math>A</math> auf dem Graphen von <math>f</math> so variiert auch der Punkt <math>M</math> und die Spur des Punktes <math>M</math> gibt den Graphen der Ableitungsfunktion <math>f'</math> wieder. | ||
| + | |||
| + | |||
| + | [http://wiki.zum.de/Mathematik-digital/Zusammenhang_zwischen_Graph_einer_Funktion_und_Ableitung Zusammenhang zwischen Funktion und 1. Ableitung]<br> | ||
[http://www.matheprisma.uni-wuppertal.de/Module/Ableitung/Seite10.htm Überblick über die Ableitungsregeln mit Beispielen]<br> | [http://www.matheprisma.uni-wuppertal.de/Module/Ableitung/Seite10.htm Überblick über die Ableitungsregeln mit Beispielen]<br> | ||
| Zeile 46: | Zeile 49: | ||
[http://www.mathe-online.at/tests/diff1/poldiff.html multiple-choice]<br> | [http://www.mathe-online.at/tests/diff1/poldiff.html multiple-choice]<br> | ||
[http://www.mathe-online.at/tests/diff1/ablerkennen.html Ableitungspuzzle]<br> | [http://www.mathe-online.at/tests/diff1/ablerkennen.html Ableitungspuzzle]<br> | ||
| − | |||
| − | |||
[http://www.frustfrei-lernen.de/mathematik/ableitung-produktregel-quotientenregel-ableitungsregel.html Produkt- und Quotientenregel]<br> | [http://www.frustfrei-lernen.de/mathematik/ableitung-produktregel-quotientenregel-ableitungsregel.html Produkt- und Quotientenregel]<br> | ||
Version vom 7. November 2014, 15:03 Uhr
Inhaltsverzeichnis |
Wiederholung
Grundlegende Fertigkeiten, die man zu Beginn der Oberstufe haben sollte
Tafelmitschriften
14. , 16. und 17.10, 
21.10. , 
23.10.
24.10. , 
4.11. , 
6.11.
7.11.
Gebrochen-rationale Funktionen
Wiederholung rationalen Funktionen: rationale Funktionen, Hyperbeln
Die Ableitungsfunktion
Von der Sekantensteigung zur Tangentensteigung:
Mit dem Schieberegler für h kann man den x-Abstand h des Punktes B vom Punkt A ändern. Geht h gegen 0 so wird aus der Sekante [AB] die Tangente in A an den Graphen der Funktion f.
Lernpfad: Einführung in die Differentialrechnung
Wissen:Ableitung, Differentialquotient
Die Ableitungsfunktion f'
Gegeben ist die Polynomfunktion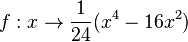 
.
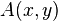ist ein Punkt auf dem Graphen von 
. In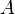 
ist die Tangente an den Graphen von , diese hat die Steigung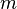 
. Trägt man über jeden x-Wert von 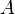den Steigungswert 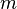an, so erhält man den Punkt 
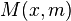. Bewegt man nun den Punkt 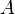auf dem Graphen von so variiert auch der Punkt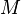 
und die Spur des Punktes 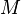gibt den Graphen der Ableitungsfunktion 
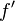wieder.
Zusammenhang zwischen Funktion und 1. Ableitung
Überblick über die Ableitungsregeln mit Beispielen
multiple-choice
Ableitungspuzzle
Produkt- und Quotientenregel
Aufgaben zur Quotientenregel
