Rechnen mit Größen: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Auf dieser Seite kannst du das Rechnen mit Größen üben. Eine Größe ist ein Produkt aus einer Zahl und ihrer Einheit. <br> Größen bestehen also immer …“) |
|||
| Zeile 10: | Zeile 10: | ||
Beispiele: <math>s = v \cdot t,</math>, <math>F = m \cdot a,</math> <math>E_B = \frac{1}{2} \cdot m \cdot v^2</math> | Beispiele: <math>s = v \cdot t,</math>, <math>F = m \cdot a,</math> <math>E_B = \frac{1}{2} \cdot m \cdot v^2</math> | ||
| − | Man muss beim Rechnen mit Größen richtig mit den Zahlen und mit den Einheiten umgehen. Bei Aufgaben in der Physik hat man oft eine Gleichung mit den Buchstaben der vorkommenden Größen. Man löst diese Gleichung allgemein nach dem Buchstaben der gesuchten Größe auf und setzt dann erst die Zahlen mit ihren Einheiten ein. Es ist immer sinnvoll die Einheiten mitzunehmen und auch damit zu rechnen, da man dann an der Einheit des Ergebnisses schon erkennt, ob man wohl richtig gerechnet hat. Stimmt die Einheit des Ergebnisses nicht, dann ist irgendwo ein Fehler. | + | Man muss beim Rechnen mit Größen richtig mit den Zahlen und mit den Einheiten umgehen. Bei Aufgaben in der Physik hat man oft eine Gleichung mit den Buchstaben der vorkommenden Größen. Man löst diese Gleichung allgemein nach dem Buchstaben der gesuchten Größe auf und setzt dann erst die Zahlen mit ihren Einheiten ein. Es ist immer sinnvoll die Einheiten mitzunehmen und auch damit zu rechnen, da man dann an der Einheit des Ergebnisses schon erkennt, ob man wohl richtig gerechnet hat. Stimmt die Einheit des Ergebnisses nicht, dann ist irgendwo in der Rechnung ein Fehler. |
| + | |||
| + | |||
| + | Umrechnen von Einheiten: [http://www.walter-fendt.de/m14d/umrechnung.htm Das Riesenrad] und [http://www.arndt-bruenner.de/mathe/scripts/einheitenueben.htm Üben] | ||
Version vom 5. April 2016, 16:54 Uhr
Auf dieser Seite kannst du das Rechnen mit Größen üben.
Eine Größe ist ein Produkt aus einer Zahl und ihrer Einheit.
Größen bestehen also immer aus zwei Bestandteilen, einem Zahlenwert und aus der Einheit der Größe.
In der Physik sind Größen messbare Eigenschaften eines Objektes.
Beispiele: 1 und 2
Größen werden oft durch Buchstaben abgekürzt. Zwischen Größen bestehen Zusammenhänge, welche durch Gleichungen beschrieben werden.
Beispiele: 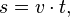 ,
, 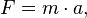
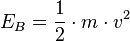
Man muss beim Rechnen mit Größen richtig mit den Zahlen und mit den Einheiten umgehen. Bei Aufgaben in der Physik hat man oft eine Gleichung mit den Buchstaben der vorkommenden Größen. Man löst diese Gleichung allgemein nach dem Buchstaben der gesuchten Größe auf und setzt dann erst die Zahlen mit ihren Einheiten ein. Es ist immer sinnvoll die Einheiten mitzunehmen und auch damit zu rechnen, da man dann an der Einheit des Ergebnisses schon erkennt, ob man wohl richtig gerechnet hat. Stimmt die Einheit des Ergebnisses nicht, dann ist irgendwo in der Rechnung ein Fehler.
Umrechnen von Einheiten: Das Riesenrad und Üben

