M8 Bruchgleichungen: Unterschied zwischen den Versionen
| Zeile 184: | Zeile 184: | ||
Bei Level 8 sind Funktionsgraphen gegeben. Da musst du zuerst die zum Funktionsterm passenden Graphen finden und dann den Schnittpunkt angeben.}} | Bei Level 8 sind Funktionsgraphen gegeben. Da musst du zuerst die zum Funktionsterm passenden Graphen finden und dann den Schnittpunkt angeben.}} | ||
| − | Bruchgleichungen kommen auch häufig in Knobelaufgaben oder Textaufgaben vor. | + | |
| + | Bruchgleichungen kommen auch häufig in Knobelaufgaben oder Textaufgaben vor. Also auch hierzu ein paar Aufgaben. | ||
{{Aufgaben-blau|8|2=1. Auf [http://ne.lo-net2.de/selbstlernmaterial/m/s1al/lbg/lbg_zr_kt1.pdf dieser Seite] sind ein paar Knobelaufgaben als Klapptest. Bearbeite dort die Aufgaben 1 bis 4. Drucke dir die Seite aus. Falte die Seite entlang der Linie. Löse die Aufgaben und vergleiche dann mit den Lösungen auf dem rechten, umgeklappten Teil der Seite. | {{Aufgaben-blau|8|2=1. Auf [http://ne.lo-net2.de/selbstlernmaterial/m/s1al/lbg/lbg_zr_kt1.pdf dieser Seite] sind ein paar Knobelaufgaben als Klapptest. Bearbeite dort die Aufgaben 1 bis 4. Drucke dir die Seite aus. Falte die Seite entlang der Linie. Löse die Aufgaben und vergleiche dann mit den Lösungen auf dem rechten, umgeklappten Teil der Seite. | ||
| Zeile 193: | Zeile 194: | ||
5. Die Lösungen sind 4 und <math>-\frac{5}{9}</math>. Da die gegebenen Zahlen natürliche Zahlen sind, kommt nur 4 in Frage.<br> | 5. Die Lösungen sind 4 und <math>-\frac{5}{9}</math>. Da die gegebenen Zahlen natürliche Zahlen sind, kommt nur 4 in Frage.<br> | ||
6. Die Lösungen sind -8 und 2. }} | 6. Die Lösungen sind -8 und 2. }} | ||
| + | |||
| + | {{Aufgaben-blau|9|Buch S. 127/7 }} | ||
| + | |||
| + | {{Lösung versteckt|1=[[Datei:127-7.jpg|400px]]<br> | ||
| + | a) Die Graphen von f und g1 schneiden sich in (-1;-1) und (1;1), die Graphen von h und g2 schneiden sich in (-1;1) und (1;-1). <br> | ||
| + | [[Datei:127-7a.jpg|400px]]<br> | ||
| + | Seitenlänge des Quadrats a = 2 LE; Flächeninhalt A = 4 FE; Umfangslänge u = 8 LE<br> | ||
| + | b) Die Graphen von f und g3 schneiden sich in (-2;-0,5) und (2;0,5), die Graphen von h und g4 schneiden sich in (-2;0,5) und (2;0,5).<br> | ||
| + | [[Datei:127-7b.jpg|400px]]<br> | ||
| + | Seitenlängen des Rechtecks l = 4 LE und b = 1 LE; Flächeninhalt A = 4 FE; Umfangslänge u = 10 LE<br> | ||
| + | <center>[[Datei:127-7b2.jpg|400px]]</center><br> | ||
| + | 50% des Flächeninhalts des Rechtecks aus b) liegen außerhalb des Rechtecks aus a). | ||
| + | }} | ||
| + | |||
| + | {{Aufgaben-blau|10|2=Buch S.127/8<br> | ||
| + | Buch S. 127/9 }} | ||
| + | |||
| + | {{Lösung versteckt|1=S. 127/8<br> | ||
| + | a) Ist x = 0, dann ist der Zähler 6x = 0, also a = 0.<br> | ||
| + | b) Ist x = 3, dann hat der Bruch den Wert <math>\frac{18}{9}=2</math>, also ist a = 2.<br> | ||
| + | c) Ist x = -6, dann hat der Bruch den Wert <math>\frac{-36}{9}=-4</math>, also ist a = -4.<br> | ||
| + | d) Ist x = -1, dann hat der Bruch den Wert <math>\frac{-6}{1}=-6</math>, also ist a = -6.<br> | ||
| + | e) Für x = -1,5 ist der Bruch nicht definiert, also hat die Gleichung keine Lösung. a kann hier beliebige Werte annehmen. | ||
| + | |||
| + | S. 127/9<br> | ||
| + | Die Gleichung <math>\frac{x}{x-1}=1+\frac{1}{x-1}</math> kann man umformen, indem man die rechte Seite der Gleichung als einen Bruch schreibt. Es ist <math>1+\frac{1}{x-1}=\frac{x-1}{x-1}+\frac{1}{x-1}=\frac{x-1+1}{x-1}=\frac{x}{x-1}=</math>. Damit hat man auf der linken und rechten Seite der Gleichung denselben Term, die Gleichung ist für alle <math>x \in D</math> richtig und es ist D = Q\{1}.<br> | ||
| + | <center>[[Datei:127-9.jpg|400px]]</center><br> | ||
| + | a) Die Graphen schneiden sich bei x = -1.<br> | ||
| + | b) Die Graphen schneiden sich bei x = 0.<br> | ||
| + | c) Die Graphen schneiden sich bei x = 0.<br> | ||
| + | d) Die Graphen schneiden sich bei x = 2. }} | ||
| + | |||
| + | |||
| + | '''Ausblick:''' | ||
| − | |||
<center>[[Datei:Schnitt zwei Hyperbeln.jpg|Schnitt zweier Hyperbeln]]</center><br> | <center>[[Datei:Schnitt zwei Hyperbeln.jpg|Schnitt zweier Hyperbeln]]</center><br> | ||
Die zwei Graphen schneidet sich in zwei Punkten. Die Koordinaten des rechten Schnittpunkts S kann man ablesen. Es ist S(2;1). Die Koordinaten des zweiten Schnittpunkte T kann man nicht so leicht ablesen. Es könnte T(0,5;-2) sein. Aber ist man sich sicher?<br> | Die zwei Graphen schneidet sich in zwei Punkten. Die Koordinaten des rechten Schnittpunkts S kann man ablesen. Es ist S(2;1). Die Koordinaten des zweiten Schnittpunkte T kann man nicht so leicht ablesen. Es könnte T(0,5;-2) sein. Aber ist man sich sicher?<br> | ||
Version vom 4. Mai 2020, 17:08 Uhr
Zu Beginn der Bruchterme haben wir gebrochen-rationale Funktionen betrachtet. Im folgenden Bild sind die zwei Graphen der Funktionen 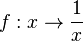 und
und 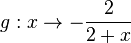 gezeichnet.
gezeichnet.
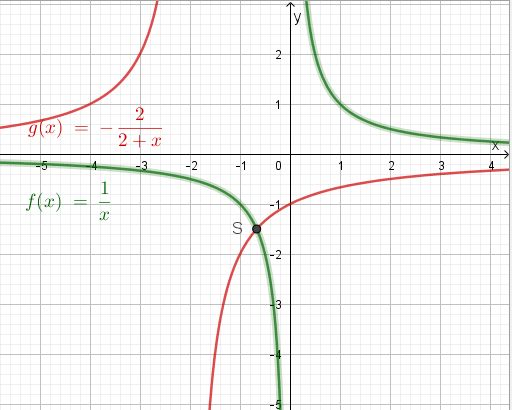
Die zwei Graphen schneidet sich in einem Punkt. Die Koordinaten des Schnittpunkts S kann man ablesen. Das Ablesen der x-Koordinate ist vage, die y-Koordinate ist besser zu erkennen. Es ist S(-0,7;-1,5). Aber ist man sich sicher?
Bei der Behandlung linearer Funktionen hatten wir auch schon den Schnittpunkt zweier Geraden. Wir haben die Geraden gezeichnet und aus dem Diagramm den Schnittpunkt abgelesen. Wir haben aber auch den Schnittpunkt berechnet, indem wir die zwei Geradengleichungen gleichgesetzt haben. Dieses Rechenverfahren wollen wir nun hier bei unseren zwei Hyperbeln auch anwenden. Im Schnittpunkt haben beide Funktionsgraphen den gleichen x- und den gleichen y-Wert. Wir setzen die beiden Funktionsterme (gleiche y-Werte) gleich 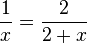 . Nun muss man diese Gleichung lösen und erhält die x-Koordinate des Schnittpunktes.
. Nun muss man diese Gleichung lösen und erhält die x-Koordinate des Schnittpunktes.
|
Merke:
Eine Bruchgleichung ist eine Gleichung mit mindestens einem Bruch, der die Unbekannte im Nenner enthält. |
Wie löst man nun die Bruchgleichung 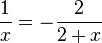 ? Wie löst man überhaupt eine Bruchgleichung?
? Wie löst man überhaupt eine Bruchgleichung?
1, Immer wenn man Bruchterme hat muss man sich zuerst überlegen, welche Zahlen man für x einsetzen darf. Das liefert die Definitionsmenge der Bruchgleichung. Hier stehen die Terme x und 2+x in den Nennern. Nenner dürfen nicht Null werden, also darf man x = 0 und x = -2 nicht einsetzen. Die Definitionsmenge hier ist also D = Q\{-2;0}.
2. Nun mulitpliziert man die Gleichung mit dem Term 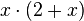 , dann erhält man
, dann erhält man
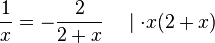
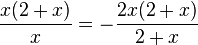
Beim Bruch auf der linken Seite der Gleichung haben Zähler und Nenner den gleichen Faktor x, beim Bruch auf der rechten Seite der Gleichung haben Zähler und Nenner den gleichen Faktor 2+x. Gleiche Faktoren kann man bei Brüchen kürzen.
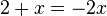
Diese Gleichung löst man und erhält als Lösung 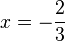 .
.
3. Nun gibt man noch die Lösungsmenge an. 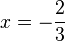 ist ein Element der Definitionsmenge (in D sind nur 0 und -2 herausgenommen). L=Q\
ist ein Element der Definitionsmenge (in D sind nur 0 und -2 herausgenommen). L=Q\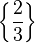 }
}
Beachte:
S. 125 b) Hier musst du erst eine Gleichung herstellen, die zwei Brüche auf den beiden Seiten des = - Zeichens hat.
Bemerkung
In den Beispielen konntest du die Bruchgleichung meist mit dem Produkt der Nenner multiplizieren. Durch Kürzen fielen die Nenner weg und du konntest eine "normale" Gleichung lösen.
Wir betrachten die Bruchgleichung: 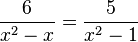 und bestimmen als Definitionsmenge D = Q\{-1;0;1}
und bestimmen als Definitionsmenge D = Q\{-1;0;1}
Wenn du die Bruchgleilchung 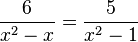 mit dem Produkt der Nenner (x2-x)(x2-1) multiplizierst, dann erhältst du:
mit dem Produkt der Nenner (x2-x)(x2-1) multiplizierst, dann erhältst du:
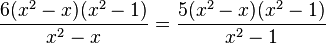 und gekürzt:
und gekürzt:
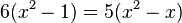 Man kann nun Vereinfachen:
Man kann nun Vereinfachen: 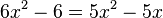 und
und 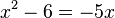 oder
oder 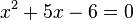 .
.
Dies ist eine quadratische Gleichung, die du nicht lösen kannst! Das lernst du erst in der 9. Klasse.
Man kann hier den Hauptnenner zum Multiplizieren der Gleichung finden, indem man sein kgV (kleinstes gemeinsame Vielfache) bestimmt.
Den Hauptnenner findest du immer als kgV (kleinstes gemeinsame Vielfache) der einzelnen Nenner.
Die Terme 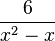 und
und 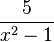 haben die Nenner x2-x und x2-1.
Beide Nenner kann man in ein Produkt umwandeln:
haben die Nenner x2-x und x2-1.
Beide Nenner kann man in ein Produkt umwandeln:
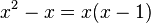 und
und 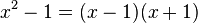
Die zweite Differenz x2-1 kann man tatsächlich so zerlegen. Überprüfe es, indem du das Produkt (x-1)(x+1) ausmultiplizierst.
Nun nimmt man alle Faktoren des nenners des Bruches auf der linken Seite, also x(x-1). Bei den Faktoren des Nenners des Bruches der rechten Seite kommt (x-1) bereits vor. Deshalb nimmt man nun nur noch (x+1) als Faktor hinzu, so dass man die Bruchgleichung mit dem Produkt x(x-1)(x+1) multipliziert.
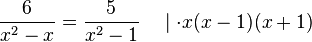
Man erhält nun diese Gleichung, dabei werden die Nenner als Produkte (, die wir uns gerade überlegt hatten) geschrieben.
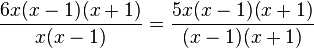
Nun kann man beim linken Bruch die gemeinsamen Faktoren x(x-1) und beim rechten Bruch die gemeinsamen Faktoren (x-1)(x+1) kürzen.
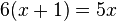 Diese Gleichung lässt sich lösen:
Diese Gleichung lässt sich lösen: 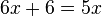 und es ist
und es ist 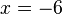 .
.
Damit erhält man tatsächlich eine Lösung, die in D enthalten ist. L = {-6}.
Du kannst gerne die Probe machen, indem du für x die gefundene Zahl -6 einsetzt:
linke Seite: 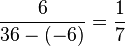 und rechte Seite:
und rechte Seite: 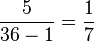
Auf beiden Seiten erhält man das gleiche Ergebnis!
Dadurch dass wir die einzelnen Bruchnenner faktorisiert haben und die Faktoren nur so oft verwendet haben wie sie in
den einzelnen Nennern vorkamen, konnten wir die Aufgabe lösen.
Du kennst diese Verfahren bereits vom Rechnen mit Brüchen. Um die Brüche 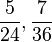 und
und 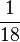 zu addieren bestimmt du auch das kgV(24,36,18) = 72 als Hauptnenner und erweiterst die Brüche nicht auf den Nenner 24·36·18=15552. Man zerlegt die Nenner in Faktoren 24 = 2·2·2·3, 36 = 2·2·3·3 und 72 = 2·2·2·3·3 und erhält als Hauptnenner 2·2·2·3·3=72.
Es ist dann
zu addieren bestimmt du auch das kgV(24,36,18) = 72 als Hauptnenner und erweiterst die Brüche nicht auf den Nenner 24·36·18=15552. Man zerlegt die Nenner in Faktoren 24 = 2·2·2·3, 36 = 2·2·3·3 und 72 = 2·2·2·3·3 und erhält als Hauptnenner 2·2·2·3·3=72.
Es ist dann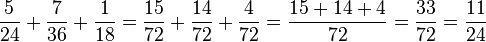 . Mit Hauptnenner 15552 muss natürlich das gleiche Ergebnis am Ende herauskommen!
. Mit Hauptnenner 15552 muss natürlich das gleiche Ergebnis am Ende herauskommen!
30px Merke
Du findest den Hauptnenner mit dem du die Bruchgleichung multiplizierst, indem du alle Faktoren der einzelnen Bruchnenner so oft für den Hauptnenner verwendest wie sie in den einzelnen Nennern vorkommen. 1. Die Nenner |
a) Der 1. Nenner ist x, der zweite Nenner ist faktorisiert (x-1)(x+1) und der dritte Nenner ist faktorisiert x(x-1).
Für den Hauptnenner verwendet man vom 1. Nenner x, vom zweiten Nenner (x-1) und (x+1) als Faktoren und hat dann x(x-1)(x+1). Nun muss man noch den dritten Nenner ansehen. Dessen zwei Faktoren x und (x+1) sind bereits vorhanden, also müssen sie nicht hinzugenommen werden.
Der Hauptnenner ist x(x-1)(x+1).
b) Man faktorisiert zurerst die Nenner: 1.Nenner 2x = 2·x, 2.Nenner x2+x = x·(x+1) und 3. Nenner x2-2x=x·(x-2)
Für den Hauptnenner verwendet man vom 1. Nenner 2·x, vom zweiten Nenner ist x schon vorhanden und man nimmt nur noch (x+1) hinzu und vom dritten Nenner ist x auch schon vorhanden und es kommt noch (x-2) dazu.
Auf dieser Seite ist das Lösen von Bruchgleichungen nochmals an Beispielen erklärt.
Beachte, dass man bei Mengen die kleinere Zahl immer zuerst schreibt!<br>
Zum Beispiel {-6; -4; -2,3; -0,7;0;0,3;1,1;1,7;2,3;2,4;9}
S. 126/1
a) D = Q\{-5}; multiplziere die Gleichung mit (x+5). Du erhältst 4 = x+5 und als x = -1; L={-1}
b) D=Q\{3}; x = 6,5; L={6,5}
c) D=Q\/-1,5}; x = -1; L={-1}
d) D=Q\{1,5}; x = 1,45; L={1,45}
e) Hauptnenner ist 2x. Multipliziere die Gleichung mit 2x. Es ist dann 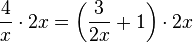
Vereinfache beide Seiten: 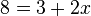 und
und 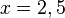 . L={2,5}
. L={2,5}
f) Dies ist keine Bruchgleichung! Also einfaches Lösen ergibt x = 100.
g) D=Q\{0;2}; Hauptnenner ist x(x-2); x = 2; 2 ist kein Element von D, also L={}
h) D=Q\{0}; x = 1; L={1}
i) keine Bruchgleichung; x = 15
j) D=Q\[-5}; x = 3; L={3}
k) D=Q\{-4;3}; 7 = 7 (allgemeingültige Gleichung, also L=Q\{-4;3}
l) D=Q\{-3;0}, x = -2,5; L ={-2,5}
m) D=Q\{-2;-1}; x=0,5; L={0,5}
n) D=Q\{0}; x = ±1; L={-1;1}
o) D=Q\-1;0}; Hauptnenner ist 4x(x+1); x = 1,4; L={1,4}
p) D=Q\{0}; x=0; L={}
S. 126/2
Hier sind Zahlen gemeint, die man erst gar nicht einsetzen darf, bei denen der Nenner den Wert 0 annehmen würde.
a) 0 ist keine Lösung der Gleichung. Ist 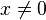 , dann kann man die Gleichung nach x auflösen und erhält
, dann kann man die Gleichung nach x auflösen und erhält 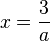 . Dies ist, da
. Dies ist, da 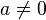 ist stets eine Lösung.
ist stets eine Lösung.
b) 1 ist keine Lösung der Gleichung. Ist 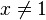 , dann kann man die Gleichung nach x auflösen und erhält
, dann kann man die Gleichung nach x auflösen und erhält 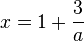 . Dies ist, da
. Dies ist, da 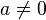 ist stets eine Lösung.
ist stets eine Lösung.
c) 5 ist keine Lösung der Gleichung. Ist 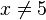 , dann kann man die Gleichung nach x auflösen und erhält
, dann kann man die Gleichung nach x auflösen und erhält 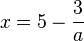 . Dies ist, da
. Dies ist, da 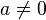 ist stets eine Lösung.
ist stets eine Lösung.
d) 0 und 1 sind keine Lösungen der Gleichung. Ist 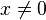 und
und 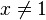 , dann kann man die Gleichung nach x auflösen und erhält
, dann kann man die Gleichung nach x auflösen und erhält 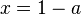 . Dies ist stets eine Lösung.
. Dies ist stets eine Lösung.
e) -2 ist keine Lösung der Gleichung. Ist 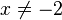 , dann kann man die Gleichung nach x auflösen und erhält
, dann kann man die Gleichung nach x auflösen und erhält 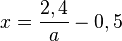 . Dies ist, da
. Dies ist, da 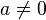 ist stets eine Lösung.
ist stets eine Lösung.
S. 126/3
Für alle Aufgaben ist D=Q\{-1}.
a) x = 0, L={0}
b) falsche Aussage 0=1, also L={}
c) x = -0,5; L={-0,5}
d) x=0, also L={0}
S. 126/4
a) D=Q\{-6;-4}; Multiplikation mit dem Hauptnenner (6+x)(x+4) liefert (4+x)2=(6+x)2 und ausmultipliziert
16 + 8x + x^2 = 36 + 12x + x^2 .
Vereinfacht erhält man -4x = 20 und x = -5, also L={-5}
b) D=Q; x = 144; L={144}
c) D=Q\{0}; x = 90000, L={90000}
 , was nicht erlaubt ist. x = 7,5; L={7,5}
, was nicht erlaubt ist. x = 7,5; L={7,5}
S. 126/5
a) Damit der Bruch den Wert 1 hat, muss der Nenner des Bruches 6 sein, also x = 5.
b) Damit der Bruch den Wert 2 hat, muss der Nenner des Bruches 3 sein, also x = 3.
c) Damit der Bruch den Wert 3 hat, muss der Nenner des Bruches 2 sein, also x = 1.
d) Damit der Bruch den Wert 4 hat, muss der Nenner des Bruches 1,5 sein, also x = 0,5.
e) Damit der Bruch den Wert 6 hat, muss der Nenner des Bruches 1 sein, also x = 0.
f) Damit der Bruch den Wert 12 hat, muss der Nenner des Bruches 0,5 sein, also x = -0,5.
g) Damit der Bruch den Wert 60 hat, muss der Nenner des Bruches 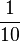 sein, also
sein, also 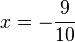 .
.
h) Ein Bruch hat den Wert 0, wenn der Zähler des Bruches den Wert 0 hat.
Der Zähler hat den Wert 60, also kann der Bruch nie den Wert 0 haben.
S. 126/6
Ein Produkt hat den Wert 0, wenn ein Faktor den Wert 0 hat!
a) Der 1. Faktor hat für x = 3 den Wert 0, der zweite Faktor hat für x = 2 den Wert 0, also hat das Produkt für x = 3 oder x = 2 den Wert 0. L={2;3}
b) Der 1. Faktor hat für x = 2 den Wert 0, der zweite Faktor hat für x = 8 den Wert 0, also hat das Produkt für x = 2 oder x = 8 den Wert 0. L={2;8}
c) Der 1. Faktor hat für x = -4 den Wert 0, der zweite Faktor hat für x = 4 den Wert 0, also hat das Produkt für x = -4 oder x = 4 den Wert 0. L={-4;4}
Ein Bruch hat den Wert 0, wenn der Zähler den Wert 0 hat.
d) D=Q\{-2}. Der Zähler hat für x = 0 den Wert 0. L={0}
e) D=Q\{0}. Der Zähler hat für x = ±6 den Wert 0. L={-6;6}
f) D=Q\{-3;3}. Der Zähler hat nie 0 den Wert 0 (Es ist x2+1 ≥ 1.). L={}
Bruchgleichungen kommen auch häufig in Knobelaufgaben oder Textaufgaben vor. Also auch hierzu ein paar Aufgaben.
1. Bei den Aufgaben 5 und 6 erhältst du eine quadratische Gleichung, die du noch nicht lösen kannst.
5. Die Lösungen sind 4 und 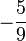 . Da die gegebenen Zahlen natürliche Zahlen sind, kommt nur 4 in Frage.
. Da die gegebenen Zahlen natürliche Zahlen sind, kommt nur 4 in Frage.
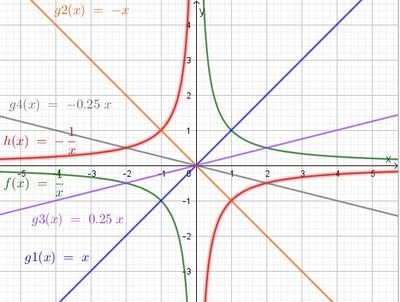
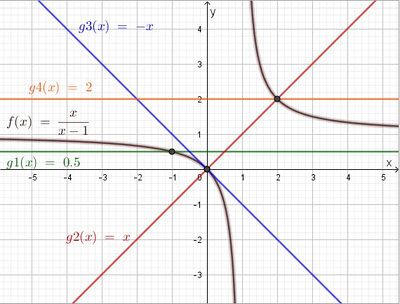
a) Die Graphen von f und g1 schneiden sich in (-1;-1) und (1;1), die Graphen von h und g2 schneiden sich in (-1;1) und (1;-1).
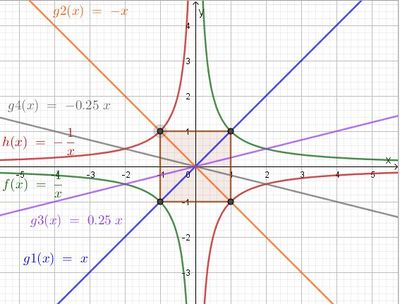
Seitenlänge des Quadrats a = 2 LE; Flächeninhalt A = 4 FE; Umfangslänge u = 8 LE
b) Die Graphen von f und g3 schneiden sich in (-2;-0,5) und (2;0,5), die Graphen von h und g4 schneiden sich in (-2;0,5) und (2;0,5).
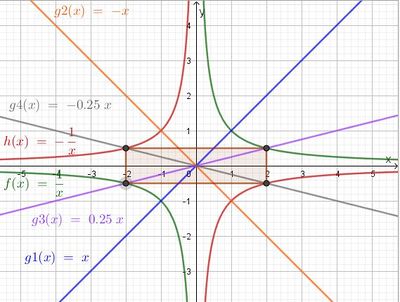
Seitenlängen des Rechtecks l = 4 LE und b = 1 LE; Flächeninhalt A = 4 FE; Umfangslänge u = 10 LE
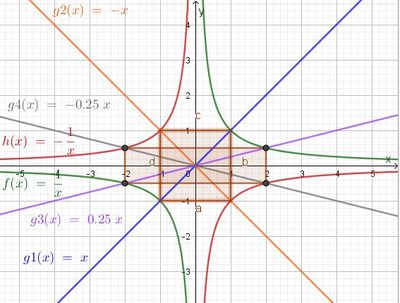
50% des Flächeninhalts des Rechtecks aus b) liegen außerhalb des Rechtecks aus a).
S. 127/8
a) Ist x = 0, dann ist der Zähler 6x = 0, also a = 0.
b) Ist x = 3, dann hat der Bruch den Wert 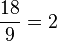 , also ist a = 2.
, also ist a = 2.
c) Ist x = -6, dann hat der Bruch den Wert 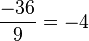 , also ist a = -4.
, also ist a = -4.
d) Ist x = -1, dann hat der Bruch den Wert 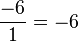 , also ist a = -6.
, also ist a = -6.
e) Für x = -1,5 ist der Bruch nicht definiert, also hat die Gleichung keine Lösung. a kann hier beliebige Werte annehmen.
S. 127/9
Die Gleichung 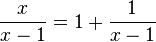 kann man umformen, indem man die rechte Seite der Gleichung als einen Bruch schreibt. Es ist
kann man umformen, indem man die rechte Seite der Gleichung als einen Bruch schreibt. Es ist 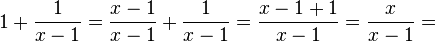 . Damit hat man auf der linken und rechten Seite der Gleichung denselben Term, die Gleichung ist für alle
. Damit hat man auf der linken und rechten Seite der Gleichung denselben Term, die Gleichung ist für alle 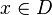 richtig und es ist D = Q\{1}.
richtig und es ist D = Q\{1}.
a) Die Graphen schneiden sich bei x = -1.
b) Die Graphen schneiden sich bei x = 0.
c) Die Graphen schneiden sich bei x = 0.
Ausblick:
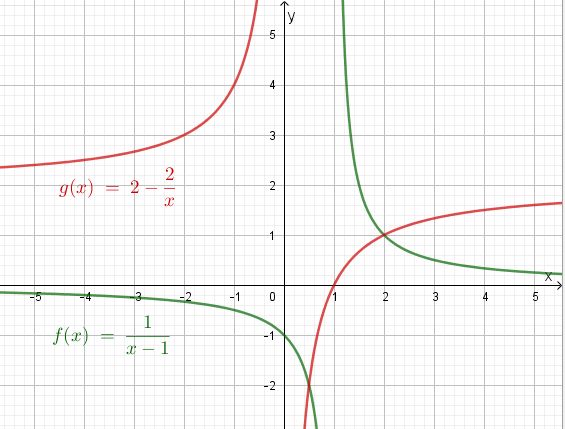
Die zwei Graphen schneidet sich in zwei Punkten. Die Koordinaten des rechten Schnittpunkts S kann man ablesen. Es ist S(2;1). Die Koordinaten des zweiten Schnittpunkte T kann man nicht so leicht ablesen. Es könnte T(0,5;-2) sein. Aber ist man sich sicher?
Eine Überprüfung wäre hier durch Einsetzen von x im Funktionsterm möglich. Wenn der richtige y-Wert herauskommt, dann hat man die richtigen Koordinaten des Schnittpunkts. Es ist f(2)= 1 = g(2) und f(0,5) = -1 = g(0,5). Also richtig abgelesen!
Bei der Behandlung linearer Funktionen hatten wir auch schon den Schnittpunkt zweier Geraden. Wir haben die Geraden gezeichnet und aus dem Diagramm den Schnittpunkt abgelesen. Wir haben aber auch den Schnittpunkt berechnet, indem wir die zwei Geradengleichungen gleichgesetzt haben. Dieses Rechenverfahren wollen wir nun hier bei unseren zwei Hyperbeln auch anwenden. Im Schnittpunkt haben beide Funktionsgraphen den gleichen x- und den gleichen y-Wert. Wir setzen die beiden Funktionsterme (gleiche y-Werte) gleich 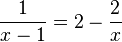 . Nun muss man diese Gleichung lösen und erhält die x-Koordinate des Schnittpunktes.
. Nun muss man diese Gleichung lösen und erhält die x-Koordinate des Schnittpunktes.
Man muss die Glelichung 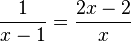 lösen.
lösen.
1. Man bestimmt die Definitionsmenge. In den Nennern stehen die Terme x-1 und x. Nenner dürfen nicht Null werden, also darf man x = 1 und x = 0 nicht einsetzen. Die Definitionsmenge hier ist also D = Q\{0;1}.
Nun kann man daran gehen die Gleichung 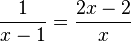 zu lösen. Was bei Bruchgleichungen immer stört sind die Brüche. Mulitpliziert man die Gleichung mit dem Term (x-1)x, dann erhält man
zu lösen. Was bei Bruchgleichungen immer stört sind die Brüche. Mulitpliziert man die Gleichung mit dem Term (x-1)x, dann erhält man
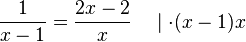
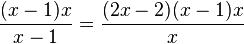
Im Zähler und Nenner des Bruchs auf der linken Seite der Gleichung steht der gleiche Faktor x-1 und auf der rechten Seite der
Gleichung der gleiche Faktor x. Gleiche Faktoren kann man kürzen!
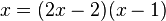
Dies ist eine Gleichung, die man nun lösen muss.
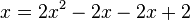
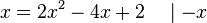
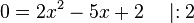
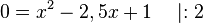
Diese Art von Gleichung lernst du in der 9. Klasse zu lösen. Aber wir haben ja schon zwei Lösungen x = 2 und x = 0,5.
Setzt man für x diese Werte ein, dann ist die Gleichung richtig.
Man kann den Term 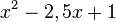 auch als Produkt schreiben:
auch als Produkt schreiben: 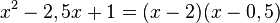 .
.
(Multipliziere das Produkt 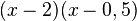 aus, dann erhältst du den Term auf der linken Seite
aus, dann erhältst du den Term auf der linken Seite 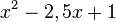
Ein Produkt hat den Wert 0, wenn ein Faktor den Wert 0 annimmt. Der erste Faktor x-2 hat für x = 2 den Wert 0,
der zweite Faktor x-0,5 hat für x = 0,5 den Wert 0. Das sind unsere beiden Lösungen vom Ablesen am Graphen.
Zuletzt gibt man noch die Lösungsmenge an: L = {0,5; 2}

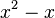 und
und 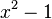 werden faktorisiert:
werden faktorisiert: 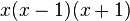 .
.

