M9 Quadratische Gleichungen: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „__NOCACHE__ Bei den linearen Funktionen war es nützlich die Schnittpunkte des Graphen mit den Koordinatenachsen zu bestimmen. Der Schnittpunkt mit der y-Achse…“) |
Version vom 5. Januar 2021, 09:40 Uhr
Bei den linearen Funktionen war es nützlich die Schnittpunkte des Graphen mit den Koordinatenachsen zu bestimmen. Der Schnittpunkt mit der y-Achse war der y-Abschnitt t und mit Hilfe der Nullstelle (Schnittpunkt mit der x-Achse) konnte man leicht die Steigung mbestimmen.
Bei den quadratischen Funktionen geht dies ähnlich. Der Schnittpunkt mit der y-Achse ist durch f(0) gegeben. Die Nullstelle/Nullstellen erhält man durch Lösen der Gleichung f(x) = 0.
Bei den Übungen zu den quadratischen Funktionen hast du bei Aufgabe 1 und Aufgabe 2 gesehen, dass eine Parabel zwei Nullstellen oder keine Nullstelle haben kann. Von der Normalparabel kennst du, dass sie eine Nullstelle hat.
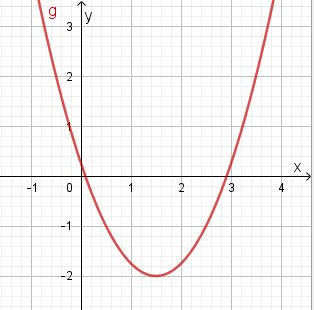
Manchmal kann man aus dem Graph die Nullstellen direkt ablesen. Man spricht dann vom graphischen Lösen der quadratischen Gleichung. Bei der quadratischen Funktion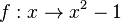 
hast du folgenden Graph
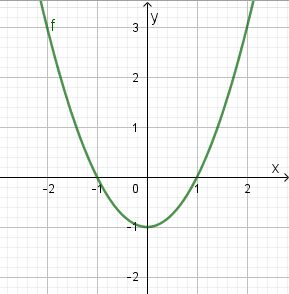
Du liest hier problemlos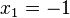 
und 
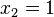als Nullstellen der Funktion ab.
%5E2-1.jpg)
%5E2%2B1.jpg)
%5E2-2.jpg)
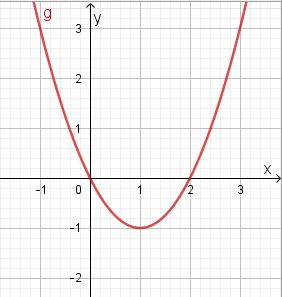
a) x1 = 0 und x2 = 2, y = (x-1)2-1
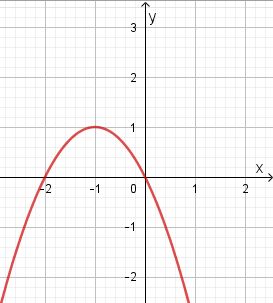
b) x1 = -2 und x2 = 0, y = -(x+1)2+1
