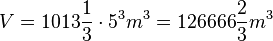M11 Aufgabe zu dreimensionalem Koordinatensystem: Unterschied zwischen den Versionen

Aus RSG-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Buch S. 88 / 1 {{Lösung versteckt|1=F liegt in der x<sub>1</sub>x<sub>2</sub>-Ebene (x<sub>3</sub>-Koordinate ist 0) und hat die Entfernung 5 zum Ursprung.<b…“)
 
Zeile 37: Zeile 37:
 
Die Höhe des Tetraeder hat die Länge <math>2 \sqrt 6</math>, da die Punkte R I und S in der x<sub>1</sub>x<sub>2</sub>-Ebene liegen und der Abstand von S von der x<sub>1</sub>x<sub>2</sub>-Ebene ist seine x<sub>3</sub>-Koordinate.<br>
 
Die Höhe des Tetraeder hat die Länge <math>2 \sqrt 6</math>, da die Punkte R I und S in der x<sub>1</sub>x<sub>2</sub>-Ebene liegen und der Abstand von S von der x<sub>1</sub>x<sub>2</sub>-Ebene ist seine x<sub>3</sub>-Koordinate.<br>
 
<math>O \approx 62,85</math>}}
 
<math>O \approx 62,85</math>}}
 +
 +
Buch S. 89 / 9
 +
 +
{{Lösung versteckt|1=a) A(0;-4;0), R(-4;0,0), L(0;24;0), T(-4;20;0), I(0;20;10)<br>
 +
b) <math>\alpha = 68^o</math>, <math>V = 1013 \frac{1}{3} \cdot 5^3 m^3 =126666 \frac{2}{3} m^3</math> }}

Version vom 9. Januar 2021, 15:31 Uhr

Buch S. 88 / 1

F liegt in der x1x2-Ebene (x3-Koordinate ist 0) und hat die Entfernung 5 zum Ursprung.
E liegt auf der xx-Achse und hat die Entfernung 4 zum Ursprung.
R liegt auf der x3-Achse und hat die Entfernung 8 zum Ursprung.
M liegt in der x2x3-Ebene und hat die Entfernung 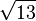\sqrt {13} zum Ursprung.
A liegt in der x1x3-Ebene und hat die Entfernung 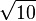\sqrt {10} zum Ursprung.
T liegt auf der x1-Achse und hat die Entfernung 5 zum Ursprung.

A ist dem Ursprung am nächsten und R am weitesten entfernt.

Buch S. 88 / 4

a) Die Punkte P liegen wegen x3=0 in der x1x2-Ebene. Die x1-Koordinate ist a, die x2Koordinate ist 2a. Eretzt man nun in der x2-Koordinate a durch x1, so ist x2 = 2x1. Mit den Bezeichnungen der Mittelstufe ist dies y = 2x, also in der x1x2-Ebene die Gerade mit der Gleichung x2 = 2x1.

b) Die Punkte P liegen, da x1=0 ist, in der x2x3-Ebene. Ersetzt man hier bei x3=x2 a durch x2, so ist x3=x22. Dies ist in der x2x3-Ebene eine Normalparabel.

c) Die Punkte P liegen wegen x1=0 in der x2x3-Ebene. Ersetzt man in x3= 1/a a durch x2 so erhält man 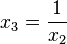x_3=\frac{1}{x_2}. Dies ist in der x2x3-Ebene eine Hyperbel.

d) Die Punkte P liegen wegen x2=0 in der x1x3-Ebene. Ersetzt man in x3=2a-1 a durch x1 so erhält man x3=21-1. Dies ist in der x1x3-Ebene eine Gerade.

Buch S.89 / 5

R(2;-2;0), H(2;2;0), A(-2;2;0), E(-2;-2;0) T((2;-2;4), H(2;2;4), A(-2;2;4), E(-2;-2;4), S(0;0;7)
V = VWürfel + VPyramide = 43 + 1/2· 42 ·3=80 (VE)

b) S(4;-4;0), T(4;4,0), E(0;4;0), V(0;-4;0), I(0;-4,3), N(0;4;3)
S*(-4;4;0), T*(-4;4;0)
O = 8·8 + 2·(8·5) + 2·(0,5·(8·3))=168 (FE)

V = 0,5·8·3·8 96

Buch S. 89 / 7

Jede Kante hat die Länge 6.
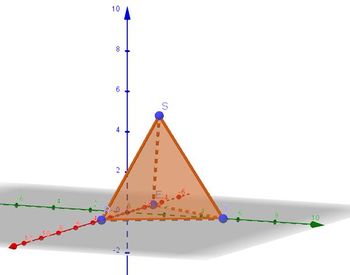
89-7.jpg
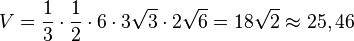
V=\frac{1}{3} \cdot \frac{1}{2}\cdot 6 \cdot 3 \sqrt 3 \cdot 2 \sqrt 6 = 18 \sqrt 2 \approx 25,46
Die Höhe des Tetraeder hat die Länge 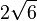2 \sqrt 6, da die Punkte R I und S in der x1x2-Ebene liegen und der Abstand von S von der x1x2-Ebene ist seine x3-Koordinate.

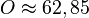
O \approx 62,85

Buch S. 89 / 9

a) A(0;-4;0), R(-4;0,0), L(0;24;0), T(-4;20;0), I(0;20;10)

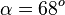b) \alpha = 68^o, V = 1013 \frac{1}{3} \cdot 5^3 m^3 =126666 \frac{2}{3} m^3
Von „http://rsg.zum.de/index.php?title=M11_Aufgabe_zu_dreimensionalem_Koordinatensystem&oldid=10817“