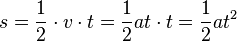Ph9 tx- und tv- Abhängigkeiten: Unterschied zwischen den Versionen
| Zeile 112: | Zeile 112: | ||
}} | }} | ||
| − | {{Aufgaben-blau|6|2=1. Schaue dir [https://www.leifiphysik.de/mechanik/lineare-bewegung-gleichungen/grundwissen/zeit-orts-diagramm auf dieser Seite] | + | {{Aufgaben-blau|6|2=1. Schaue dir das Applet [https://www.leifiphysik.de/mechanik/lineare-bewegung-gleichungen/grundwissen/zeit-orts-diagramm auf dieser Seite] zur Entstehung eines Zeit-Ort-Diagramms an und erkläre was ein ts-Diagramm ist. <br> |
2. Buch S. 65 / 1, 2 }} | 2. Buch S. 65 / 1, 2 }} | ||
| − | {{Lösung versteckt|1=1. In einem ts-Diagramm werden Zeit-Ort-Wertepaaren (t,s) dargestellt. Für jedes t im Zeitintervall wird der entsprechende Ort darüber aufgetragen.<br> | + | {{Lösung versteckt|1=1. In einem ts-Diagramm werden Zeit-Ort-Wertepaaren (t,s) dargestellt. Für jedes t im Zeitintervall wird der entsprechende Ort darüber aufgetragen, dabei wird die Zeit nach rechts und der Weg nach oben angetragen.<br> |
2. S.65/1 Zugrunde liegt das th-Diagramm Bild 5 auf S. 65. <br> | 2. S.65/1 Zugrunde liegt das th-Diagramm Bild 5 auf S. 65. <br> | ||
| Zeile 141: | Zeile 141: | ||
Man hat für die 0,1s-Intervalle die Durchschnittsgeschwindigkeit berechnet. Dies bedeutet, dass man in diesem Intervall mit konstanter Geschwindigkeit, eben dieser Durchschnittsgeshwindigkeit, fährt. Daher ergibt sich im Graph so eine Treppenfunktion. <br> | Man hat für die 0,1s-Intervalle die Durchschnittsgeschwindigkeit berechnet. Dies bedeutet, dass man in diesem Intervall mit konstanter Geschwindigkeit, eben dieser Durchschnittsgeshwindigkeit, fährt. Daher ergibt sich im Graph so eine Treppenfunktion. <br> | ||
e) Es ist Beschleunigung <math>a = \frac{\Delta v}{\Delta t}</math>.<br> | e) Es ist Beschleunigung <math>a = \frac{\Delta v}{\Delta t}</math>.<br> | ||
| − | <math>a_1=\frac{}{}</math> | + | <math>a_1=\frac{150cm/s - 50 cm/s}{0,1}= \frac{100cm/s}{0,1s}=1000 cm\s^2=10m/s^2</math><br> |
| + | <math>a_2=\frac{350cm/s - 50 cm/s}{0,3}= \frac{300cm/s}{0,3s}=1000 cm\s^2=10m/s^2</math><br> | ||
| + | <math>a_1=\frac{350cm/s - 250 cm/s}{0,1}= \frac{100cm/s}{0,1s}=1000 cm\s^2=10m/s^2</math><br> | ||
| + | Egal welche Kombination man wählt es kommt immer a = 10m/s² heraus.<br> | ||
| + | f) Aus c) weiß man t = 0,53s Er wird mit einer Geschwindigkeit 480 cm/s aufkommen (Dreisatz). }} | ||
| − | }} | + | {{Aufgaben-blau|7|2=Bearbeite das Quiz zu<br> |
| + | 1. [https://www.leifiphysik.de/mechanik/lineare-bewegung-gleichungen/aufgabe/quiz-zu-zeit-orts-diagrammen Zeit-Ort-Diagramm ]<br> | ||
| + | 2. [https://www.leifiphysik.de/mechanik/lineare-bewegung-gleichungen/aufgabe/reisezeiten Reisezeiten] }} | ||
Version vom 22. Januar 2021, 14:01 Uhr
Ihr habt schon zwei Arten von Bewegungen kennengelernt:
- Bewegung mit konstanter Geschwindigkeit und
- Bewegung mit konstanter Beschleunigung
Für beide Bewegungen sammeln wir zuerst unsere bisherigen Kenntnisse:
1. Gleichförmige Bewegung:
 Merke
Bei einer gleichförmigen Bewegung bewegt sich ein Körper geradlinig mit konstanter Geschwindigkeit v = konstant. 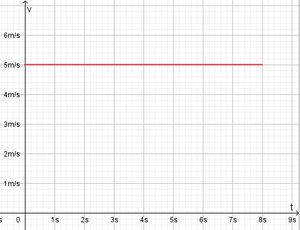 Im ts-Diagramm wird auch nach rechts die Zeit t aber nach oben der zurückgelegte Weg s aufgetragen. 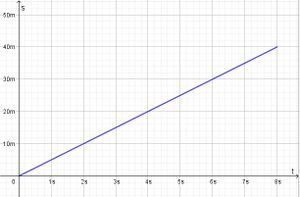 Die Strecke beginnt im Ursprung und steigt linear an. Formeln:
 |
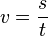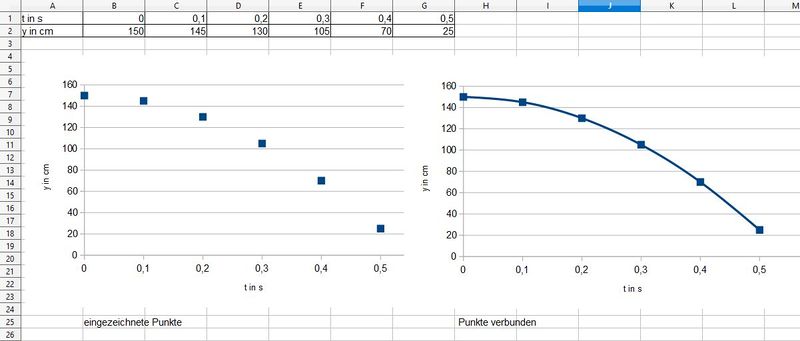
Die Fläche unter der Kurve im tv-Diagramm ist eine Rechtecksfläche und berechnet sich als v·t.
Sie stellt den zurückgelegten Weg s dar.
a) Die Bewegung verläuft für 0s ≤ t ≤ 8s ab.
v = 5 m/s
Der insgesamt zurückgelegte Weg ist s = 40m.
2. Gleichmäßig beschleunigte Bewegung:
| Merke
Bei einer gleichmäßig beschleunigten Bewegung bewegt sich ein Körper geradlinig und wird mit konstanter Beschleunigung beschleunigt. 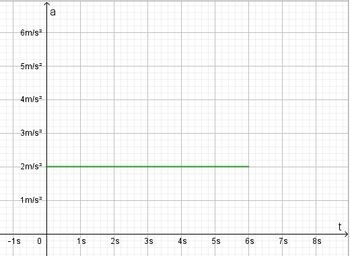 Im tv-Diagramm wird nach rechts die Zeit t und nach oben die Geschwindigkeit v aufgetragen. 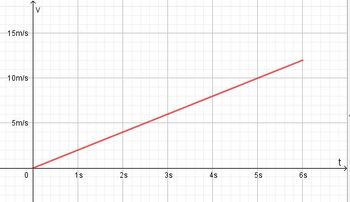 Beschleunigung 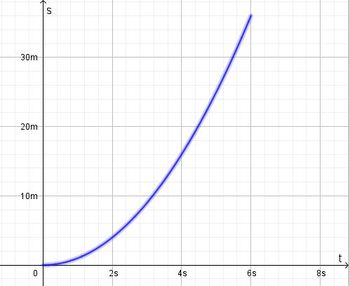 Auch hier stellt die Fläche unter dem Graph im tv-Diagramm den zurückgelegtn Weg s dar. Es ist Formeln:
 |
.
.
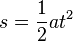a) Die Bewegung verläuft für 0s ≤ t ≤ 6s ab.
a=2m/s²
Die mach 6s erreichte Geschwindigkeit ist v = 12 m/s
Der insgesamt zurückgelegte Weg ist s = 36m.
Beachte: Die Bewegungsgleichung s = v·t darf man nicht bei der Bewegung mit konstanter Beschleunigung verwenden!
61/3 Es handelt sich um Bewegungen mit konstanter Geschwindigkeit. Im ts-Diagramm sind das Geraden. Die Geschwindigkeit gibt die Steigung der Geraden an. Je steiler die Gerade, desto größer ist die Geschwindigkeit.
a) Zeit bergab ist genauso lang wie Zeit bergauf (t-Achse), bergab steiler als bergauf --> Diagramm III
b) Strecke bergauf ist genauso lang wie Strecke bergab (s-Achse), bergauf nicht so steil wie bergab ---> Diagramm II
c) Zeit bergauf ist genauso lang wie Zeit bergab (t-Achse), bergauf nicht so steil wie bergab ---> Diagramm IV
d) Strecke bergab ist genauso lang wie Strecke bergauf (s-Achse), bergab steiler als bergauf ---> Diagramm I
61/4
Bei a) und c) jeweils gleiche Zeiten, bei b) und d) gleiche Strecken!
61/5
1. In einem ts-Diagramm werden Zeit-Ort-Wertepaaren (t,s) dargestellt. Für jedes t im Zeitintervall wird der entsprechende Ort darüber aufgetragen, dabei wird die Zeit nach rechts und der Weg nach oben angetragen.
2. S.65/1 Zugrunde liegt das th-Diagramm Bild 5 auf S. 65.
a) Nach 17s ist der Fahrstuhl in der Höhe h = 31m,
b) Bei t = 7,5s und t = 15,8s ist der Fahrstuhl bei h = 42m.
c) (3s,12m), (9s,51m) hat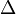 
h=39m.
In dem Intervall [3s,9s] ist der Graph eine Gerade, daher stimmt Momentangeschwindigkeit mit Durchschnittsgeschwindigkeit überein.
d) (9s, 51m), (11s,60m); 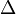h=9m und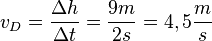 
e) Die Fahrt ist am schnellsten wo der Graph am steilsten ist (am steilsten kann auch der fallende Teil ab 14s sein.) Man legt das Geodreieck entlang des Graphen an und erkennt, dass es am steilsten t = 18,8s und t = 20s ist.
Die Plattform ist in Ruhe für 11s ≤ t ≤ 13,9s und 17,2s ≤ t ≤17,8s.
f) Graph waagrecht: es gibt keine Ortsänderungs, der Fahrstuhl ist in Ruhe
Graph geradlinig ansteigend: der Fahrstuhl fährt mit konstanter Geschwindigkeit hoch
Graph geradlinig absteigend: der Fahrstuhl fährt mit konstanter Geschwindigkeit runter
g) Graph steiler: Momentangeschwindigkeit wird größer
Graph flacher: Momentangeschwindigkeit wird kleiner
S.65/2
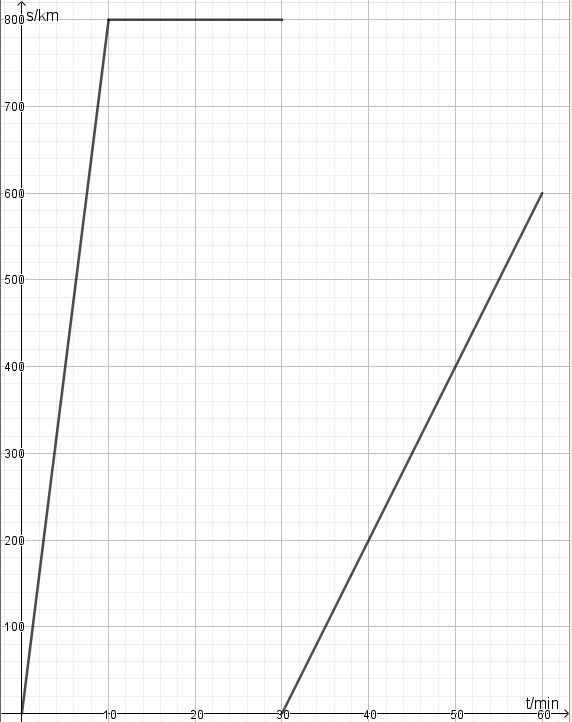
Die Punkte verbindet man im Heft, indem man sich das Heft so hinlegt, dass man mit einem Strich "aus dem Handgelenk" die Punkte
schön verbinden kann. Es sollen nicht Punkte miteinander verbunden werden, sondern es soll eine glatte Kurve ergeben.
b) Bei y = 1m geht man waagrecht nach rechts bis man den Graph trifft. Im Treffpunkt geht man dann senkrecht nach unten und liest auf der t-Achse t = 0,31 s ab.
c) Bei t = 0,15s geht man senkrecht nach oben bis man den Graph trifft. Im Treffpunkt geht man dann waagrecht nach links und liest auf der y-Achse y = 140m ab.
Verlängert man den Graph nach rechts bis man er die t-Achse trifft, dann schneidet er sie bei t=0,53 s.
d)
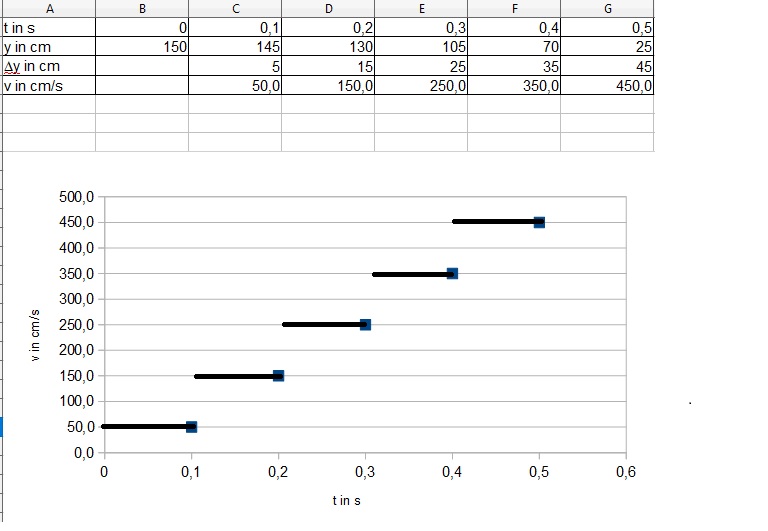
Man hat für die 0,1s-Intervalle die Durchschnittsgeschwindigkeit berechnet. Dies bedeutet, dass man in diesem Intervall mit konstanter Geschwindigkeit, eben dieser Durchschnittsgeshwindigkeit, fährt. Daher ergibt sich im Graph so eine Treppenfunktion.
e) Es ist Beschleunigung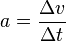 
.
Fehler beim Parsen(Unbekannte Funktion „\s“): a_1=\frac{150cm/s - 50 cm/s}{0,1}= \frac{100cm/s}{0,1s}=1000 cm\s^2=10m/s^2
Fehler beim Parsen(Unbekannte Funktion „\s“): a_2=\frac{350cm/s - 50 cm/s}{0,3}= \frac{300cm/s}{0,3s}=1000 cm\s^2=10m/s^2
Fehler beim Parsen(Unbekannte Funktion „\s“): a_1=\frac{350cm/s - 250 cm/s}{0,1}= \frac{100cm/s}{0,1s}=1000 cm\s^2=10m/s^2
Egal welche Kombination man wählt es kommt immer a = 10m/s² heraus.
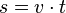
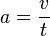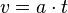