M9 Quadratische Funtkionen und Extremwerte: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „__NOCACHE__ Einem gleichseitigen Dreieck der Seitenlänge 6cm wird ein Rechteck so einbeschrieben, dass eine Rechteckseite l auf einer Dreieckseite liegt und d…“) |
Version vom 7. Februar 2021, 14:13 Uhr
Einem gleichseitigen Dreieck der Seitenlänge 6cm wird ein Rechteck so einbeschrieben, dass eine Rechteckseite l auf einer Dreieckseite liegt und die anderen Eckpunkte des Rechtecks auf den beiden anderen Dreieckseiten liegen. Im folgenden Applet ist die Situation dargestellt. Die Rechteckseite l liegt auf der Dreieckseite [AB].
Den Punkt E kann man auf der Dreieckseite [AB] bewegen. Dadurch ändert sich das Rechteck der Aufgabe. Über dem Wert der Rechteckseite l wird der Flächeninhalt 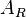 des Rechtecks aufgetragen. Dies ergibt im Applet den Punkt
des Rechtecks aufgetragen. Dies ergibt im Applet den Punkt 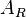 . Wenn man die Lage des Punktes E ändert, ändert sich auch die Rechteckfläche und der Punkt
. Wenn man die Lage des Punktes E ändert, ändert sich auch die Rechteckfläche und der Punkt 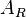 wandert. Der Punkt
wandert. Der Punkt 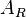 hat die Koordinaten
hat die Koordinaten 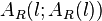
Das Rechteck hat Flächeninhalt 0, wenn l = 0 oder l = 6 ist. Gibt es ein Rechteck mit größtem Flächeninhalt?
Für den Punkt 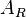 im Applet kann man die Spur anzeigen, die sich ergibt, wenn E bewegt wird. Man sieht, dass die Spur eine Parabel ergibt, deren Scheitel bei l = 3 liegt. Man kann auch den Wert von
im Applet kann man die Spur anzeigen, die sich ergibt, wenn E bewegt wird. Man sieht, dass die Spur eine Parabel ergibt, deren Scheitel bei l = 3 liegt. Man kann auch den Wert von 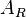 zu
zu 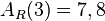 ablesen.
ablesen.
Da der Flächeninhalt 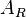 des einbeschriebenen Rechtecks von der Seitenlänge l abhängt, kann man eine Funktion
des einbeschriebenen Rechtecks von der Seitenlänge l abhängt, kann man eine Funktion 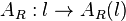 angeben, die für jeden Wert von
angeben, die für jeden Wert von ![l \in [0;6]](/images/math/f/e/8/fe8d7a0d06e68fce822e2fc4f5896284.png) den Wert
den Wert 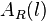 angibt. Für diese Funktion gilt es nun den Funktionsterm zu bestimmen.
angibt. Für diese Funktion gilt es nun den Funktionsterm zu bestimmen.
Der Punkt E kann vom Ursprung bis zum Mittelpunkt der Dreiecksseite [AB] gehen. Seine Koordinaten sind daher 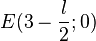 .
.
Die Dreiecksseite [AC] ist Teil einer Gerade, deren Geradengleichung y = mx + t wir bestimmen wollen. Da sie durch den Ursprung geht ist t = 0. Also müssen wir noch die Steigung m der Geraden bestimmen. Da das Dreieck ABC ein gleichseitiges Dreieck ist, wissen wir seit wir den Satz des Pythagoras kennen, dass die Höhe im gleichseitigen Dreieck mit der Seitenlänge a 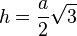 ist.
ist.
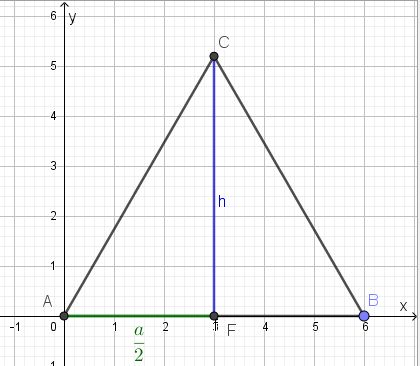
Die Steigung m ist dann 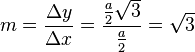
Die Gerade hat also die Gleichung 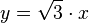 .
.
Damit können wir zur Länge l des Rechtecks nun die Breite b angeben. b geht von E senkrecht nach oben bis zur Dreiecksseite [AC]. b hat also den Wert 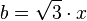 , wobei hier x die x-Koordinate des Punktes E ist, für die sich oben
, wobei hier x die x-Koordinate des Punktes E ist, für die sich oben 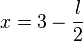 ergeben hat.
ergeben hat.
Die Rechtecksfläche ist dann 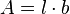 . Nun ist
. Nun ist 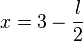 und damit
und damit 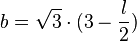 und damit
und damit 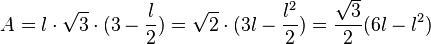 . Dies ist die Gleichung einer nach unten geöffneten Parabel, die ihre größten Wert im Scheitel annimmt.
. Dies ist die Gleichung einer nach unten geöffneten Parabel, die ihre größten Wert im Scheitel annimmt.
Die Nullstellen des Terms 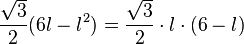 sind
sind 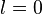 und
und 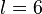 . Das hatten wir uns schon oben überlegt.
. Das hatten wir uns schon oben überlegt.
Der Scheitel der Parabel liegt genau in der Mitte zwischen den Nullstellen, also hier bei x = 3 und der Flächeninhalt des größten Rechtecks ergibt sich zu 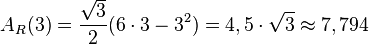 .
.
|
Merke:
Kennt man die Nullstellen x1 und x2 einer Parabel mit der Gleichung y = ax2 + bx + c, dann liegt ihr Scheitel genau in der Mitte zwischen den Nullstellen. |
Wenn man den Punkt auf der schrägen Strecke bewegt, sieht man wie sich das Rechteck ändert. Die Fläche des Rechtecks wird angezeigt und man stellt fest, dass der Flächeninhalt A des Rechtsecks am größten ist, wenn x = 85 ist und es ist A = 3400cm2.
Der obere, rechte Eckpunkt bewegt sich auf einer Geraden mit der Gleichung 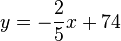 .
x kann nur Werte von 60 bis 85 annehmen, also
.
x kann nur Werte von 60 bis 85 annehmen, also ![x \in [60;85]](/images/math/b/2/8/b286be4ebb99bcd363e6d80f41d40cd1.png) .
.
Der Flächeninhalt A ist 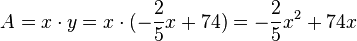 . Der Funktionsterm ist der Term einer Gleichung einer nach unten geöffneten Parabel.
. Der Funktionsterm ist der Term einer Gleichung einer nach unten geöffneten Parabel.
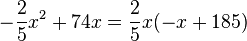 . An diesem Term sieht man leicht seine Nullstellen. Es ist
. An diesem Term sieht man leicht seine Nullstellen. Es ist 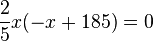 für
für 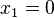 und
und 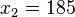 , also schneidet die Parabel die x-Achse in
, also schneidet die Parabel die x-Achse in 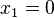 und
und 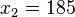 . Ihr Scheitel liegt bei
. Ihr Scheitel liegt bei 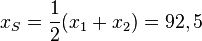 . Dieser x-Wert liegt nicht in der Definitionsmenge [60;85] für x. Da es sich um eine nach unten geöffnete Parabel handelt und die x-Werte von 60 bis 85 links vom Scheitel liegen, nehmen die Parabelwerte zum Scheitel hin zu und der größte Wert auf der Parabel ist bei x = 85 erreicht.
. Dieser x-Wert liegt nicht in der Definitionsmenge [60;85] für x. Da es sich um eine nach unten geöffnete Parabel handelt und die x-Werte von 60 bis 85 links vom Scheitel liegen, nehmen die Parabelwerte zum Scheitel hin zu und der größte Wert auf der Parabel ist bei x = 85 erreicht.
Es ist eine ähnliche Aufgabe zu Aufgabe 2, nur die Maße der Tischplatte und der abgebrochenen Ecke sind anders. Wenn man den Punkt P auf der schrägen Strecke bewegt, sieht man wie sich das Rechteck ändert. Die Fläche des Rechtecks wird angezeigt und man stellt fest, dass der Flächeninhalt A des Rechtecks, wenn P ganz oben ist A = 8100cm2 und wenn P ganz unten ist A=8400cm2 ist. Und dazwischen gibt es größere Werte als 8400cm2.
Der Punkt P sich auf einer Geraden mit der Gleichung 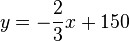 .
Die x-Koordinate von P kann nur Werte von 90 bis 120 annehmen, also
.
Die x-Koordinate von P kann nur Werte von 90 bis 120 annehmen, also ![x \in [60;85]](/images/math/b/2/8/b286be4ebb99bcd363e6d80f41d40cd1.png) .
.
Der Flächeninhalt A ist 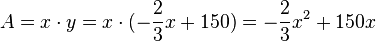 . Der Funktionsterm ist der Term einer Gleichung einer nach unten geöffneten Parabel.
. Der Funktionsterm ist der Term einer Gleichung einer nach unten geöffneten Parabel.
Der Term lässt sich umformen in 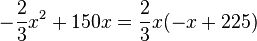 . An diesem Term sieht man leicht seine Nullstellen. Es ist
. An diesem Term sieht man leicht seine Nullstellen. Es ist 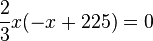 für
für 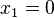 und
und 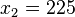 , also schneidet die Parabel die x-Achse in
, also schneidet die Parabel die x-Achse in 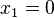 und
und 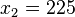 .
.
Die x-Koordinate des Scheitels 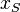 der Parabel liegt genau in der Mitte von 0 und 225, also
der Parabel liegt genau in der Mitte von 0 und 225, also 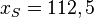 . Im Scheitel nimmt eine nach unten geöffnete Parabel ihren größen y-Wert an. Setzt man
. Im Scheitel nimmt eine nach unten geöffnete Parabel ihren größen y-Wert an. Setzt man 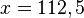 in die Gleichung
in die Gleichung 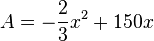 , dann erhält man
, dann erhält man 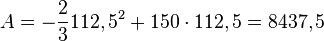 .
.


