Ph9 Der freie Fall: Unterschied zwischen den Versionen
| Zeile 19: | Zeile 19: | ||
{{Merke|1=Der freie Fall ist eine Bewegung mit konstanter Beschleunigung (ohne Berücksichtigung des Luftwiderstandes). <br> | {{Merke|1=Der freie Fall ist eine Bewegung mit konstanter Beschleunigung (ohne Berücksichtigung des Luftwiderstandes). <br> | ||
| − | Die Beschleunigung ist die Erdbeschleunigung (Ortsfaktor) <math> g = 9,8\frac{m}{s^2}</math>.<br> | + | Die Beschleunigung ist die Erdbeschleunigung (Ortsfaktor) und beträgt auf der Erdoberfläche <math> g = 9,8\frac{m}{s^2}</math>.<br> |
Die Bewegungsgleichungen sind für einen freien Fall aus der Höhe h<sub>o</sub><br> | Die Bewegungsgleichungen sind für einen freien Fall aus der Höhe h<sub>o</sub><br> | ||
| − | <center><math>v(t) = gt</math> und <math>h(t) = h_0 - \frac{1}{2}gt^2</math></center><br> | + | <center><math>v(t) = gt</math> und <math>h(t) = h_0 - \frac{1}{2}gt^2</math></center><br> }} |
| − | }} | + | |
| + | {{Aufgaben-blau|2|2=Zwischen einem Ball und der Erde wirken Gravitationskräfte. Der Ball wird von der Erde angezogen, die Erde wird aber auch vom Ball angezogen. <br> | ||
| + | a) Was weiß man über die beiden Kräfte F<sub>1</sub> mit der die Erde den Ball anzieht und F<sub>2</sub> mit der der Ball die Erde anzieht?<br> | ||
| + | b) Wie groß ist die Beschleunigung, die auf den Ball auf der Erdoberfläche wirkt?<br> | ||
| + | Was bewirkt dies beim Fallen des Balles?<br> | ||
| + | c) Wie groß ist die Beschleunigung <math>a</math>, die auf die Erde wirkt und was bewirkt sie? }} | ||
| + | |||
| + | {{Lösung versteckt|1=a) Nach dem 3. Newtonschen Gesetz sind F<sub>1</sub> und F<sub>2</sub> Kraft und Gegenkraft. Die beiden Kräfte sind gleich groß, aber entgegengesetzt gerichtet. | ||
| + | <center>{{#ev:youtube |xMILzAntAVU|350}}</center> | ||
| + | b) Die Beschleunigung, die der Ball erfährt ist <math>g=9,8\frac{m}{s^2}</math>. Diese Beschleunigung ist überall auf der Erdoberfläche gleich. <br> | ||
| + | Die Erdbeschleunigung bewirkt, dass der Ball beim Fallen schneller wird.<br> | ||
| + | b) Wegen <math>F = m\cdot a</math> ist die Beschleunigung, die auf die Erde wirkt <math>a = \frac{F}{m}</math>.<br> | ||
| + | Wegen der riesig großen Masse der Erde ist die Beschleunigung praktisch gleich <math>a = 0 \frac{m}{s^2}</math>. }} | ||
| + | |||
| + | |||
| + | <center>{{#ev:youtube |48s4Av7C3mQ|350}}</center> | ||
| + | |||
| + | {{Aufgaben-blau|3|2=Ein Stein fällt von der Höhe <br> | ||
| + | a) h<sub>o</sub> = 5m<br> | ||
| + | b) h<sub>o</sub> = 10m<br> | ||
| + | c) h<sub>o</sub> = 20m<br> | ||
| + | Wie lange dauert der Fall und mit welcher Geschwindigkeit kommt der Stein am Boden auf? }} | ||
| + | |||
| + | {{Lösung versteckt|1=Die Bewegungsgleichung <math>h(t) = h_0 - \frac{1}{2}gt^2</math> mit <math>h(t) = 0m </math> kann man nach t auflösen. Es ist <math>h_0 = \frac{1}{2}gt^2</math> und <math>t = \sqrt {\frac{2h_0}{g}}</math>.<br> | ||
| + | a) t = 1,01s<br> | ||
| + | b) t = 1,43s<br> | ||
| + | c) t = 2,02s<br> | ||
| + | Mit diesen Zeiten kann man mit der Formel <math> v = gt</math> die Auftreffgeschwindigkeit berechnen.<br> | ||
| + | a) <math>v = 9,9\frac{m}{s}</math><br> | ||
| + | b) <math>v = 14,0\frac{m}{s}</math><br> | ||
| + | c) <math>v = 19,8\frac{m}{s}</math>}} | ||
| + | |||
| + | {{Aufgaben-blau|4|2=Buch S. 80 / 3 }} | ||
| + | |||
| + | {{Lösung versteckt|1=80/3 a) <math>v= gt=9,8\frac{m}{s^2}\cdot 2s=19,6 \frac{m}{s}\approx 71\frac{km}{h}</math><br> | ||
| + | Die Durchschnittsgeschwindigkeit ist <math>v_=\frac{v_{Start}+v_{Ende}}{2}=9,8\frac{m}{s}</math>.<br> | ||
| + | Die Fallhöhe ist wegen <math>h(2s)=0m</math> durch die Gleichung <math>0m = h_0-\frac{1}{2}gt^2</math> gegeben. Man erhält <math>h_0=\frac{1}{2}gt^2=\frac{1}{2}\cdot 9,81\frac{m}{s^2}\cdot (2s)^2 = 19,6m \approx 20m</math><br> | ||
| + | Die Aussage von Hans ist wohl übertrieben. Er spricht vielleicht von "gefühlten" 2s. | ||
| + | |||
| + | b) <math>v=4,5\frac{m}{s}</math> ergibt für <math>t = \frac{v}{g}=\frac{4,5\frac{m}{s}}{9,8\frac{m}{s^2}}=0,46s</math> <br> | ||
| + | und für <math>h_0=\frac{1}{2}gt^2=\frac{1}{2}\cdot 9,8\frac{m}{s^2}\cdot (0,46s)^2= 1m</math> }} | ||
Version vom 22. Februar 2021, 17:37 Uhr
1. Der freie Fall ist eine Bewegung mit konstanter Beschleunigung ohne Berücksichtigung der Luftreibung.
2. Beim freien Fall wirkt die Erdanziehungskraft.
3. Die Beschleunigung beim freien Fall ist die Erdbeschleunigung 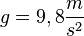 .
.
4. 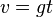 und
und 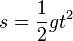 .
.
5. 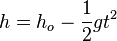 .
.
6. Die Masse m des fallenden Körpers spielt keine Rolle. Galileo Galilei zeigte, dass alle Körper gleich schnell fallen.
7. Im Vakuum fallen alle Körper gleich schnell, da dort keine Luftwiderstandskraft wirkt.
30px Merke
Der freie Fall ist eine Bewegung mit konstanter Beschleunigung (ohne Berücksichtigung des Luftwiderstandes). 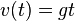 und und 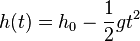 |
a) Nach dem 3. Newtonschen Gesetz sind F1 und F2 Kraft und Gegenkraft. Die beiden Kräfte sind gleich groß, aber entgegengesetzt gerichtet.
b) Die Beschleunigung, die der Ball erfährt ist 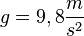 . Diese Beschleunigung ist überall auf der Erdoberfläche gleich.
. Diese Beschleunigung ist überall auf der Erdoberfläche gleich.
Die Erdbeschleunigung bewirkt, dass der Ball beim Fallen schneller wird.
b) Wegen 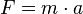 ist die Beschleunigung, die auf die Erde wirkt
ist die Beschleunigung, die auf die Erde wirkt 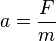 .
.
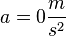 .
.
Die Bewegungsgleichung 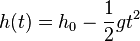 mit
mit 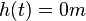 kann man nach t auflösen. Es ist
kann man nach t auflösen. Es ist 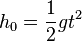 und
und 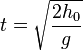 .
.
a) t = 1,01s
b) t = 1,43s
c) t = 2,02s
Mit diesen Zeiten kann man mit der Formel 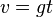 die Auftreffgeschwindigkeit berechnen.
die Auftreffgeschwindigkeit berechnen.
a) 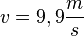
b) 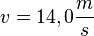
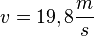
80/3 a) 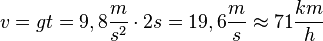
Die Durchschnittsgeschwindigkeit ist 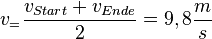 .
.
Die Fallhöhe ist wegen 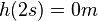 durch die Gleichung
durch die Gleichung 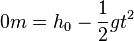 gegeben. Man erhält
gegeben. Man erhält 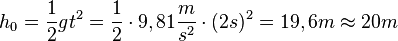
Die Aussage von Hans ist wohl übertrieben. Er spricht vielleicht von "gefühlten" 2s.
b) 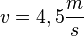 ergibt für
ergibt für 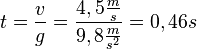
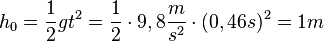
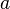 , die auf die Erde wirkt und was bewirkt sie?
, die auf die Erde wirkt und was bewirkt sie?

