M10 Eigenschaften der Exponentialfunktion: Unterschied zwischen den Versionen
Aus RSG-Wiki
(Die Seite wurde neu angelegt: „__NOCACHE__ =Die Funktion <math>f:x \rightarrow a^x</math> = {{Aufgaben-blau|1|2=Verändere die Basis a und beobachte die Auswirkungen auf den Verlauf des Gra…“) |
(→Zusammenfassung) |
||
| Zeile 36: | Zeile 36: | ||
=Zusammenfassung= | =Zusammenfassung= | ||
| − | {{Merksatz|MERK= | + | {{Merksatz|MERK=Die Exponentialfunktion <math>f:x \rightarrow b\cdot a^x</math> bzw. ihr Graph hat folgende Eigenschaften: |
| + | |||
| + | * Die Definitionsmenge aller Exponentialfunktionen ist R.<br> | ||
| + | * Es ist a > 0. | ||
| + | |||
| + | '''b = 1''' : Es geht um die Exponentialfunktion <math>f:x \rightarrow a^x</math> und ihren Graph. | ||
<center>[[Datei:Exponentialfunktion 1a.jpg|350px]]</center> | <center>[[Datei:Exponentialfunktion 1a.jpg|350px]]</center> | ||
| − | |||
| − | |||
| − | |||
| − | * | + | * <math>a^x</math> ist stets positiv. |
| − | + | ||
| + | * Alle Graphen gehen durch den Punkt (0;1)<br> | ||
* Die Graphen der Funktionen <math>f</math> mit <math>f(x) = a^x</math> und <math>g</math> mit <math>g(x) = \frac{1}{a}^x=a^{-x}</math> lliegen symmetrisch bezüglich der y-Achse. | * Die Graphen der Funktionen <math>f</math> mit <math>f(x) = a^x</math> und <math>g</math> mit <math>g(x) = \frac{1}{a}^x=a^{-x}</math> lliegen symmetrisch bezüglich der y-Achse. | ||
<center>[[Datei:Exponentialfunktion 1b.jpg|300px]]</center> | <center>[[Datei:Exponentialfunktion 1b.jpg|300px]]</center> | ||
| − | * Für 0 < a < 1 ist der Graph | + | * Für 0 < a < 1 ist der Graph monoton fallend,<br> |
* für a = 1 ist die Exponentialfunktion <math>f(x) = 1^x=1</math> konstant,<br> | * für a = 1 ist die Exponentialfunktion <math>f(x) = 1^x=1</math> konstant,<br> | ||
| − | * für a > 1 ist der Graph | + | * für a > 1 ist der Graph montoton steigend. |
* Für 0 < a < 1 nähert sich der Graph beliebig nahe an die positive x-Achse; die positive x-Achse ist Asymptote.<br> | * Für 0 < a < 1 nähert sich der Graph beliebig nahe an die positive x-Achse; die positive x-Achse ist Asymptote.<br> | ||
| − | * Für a > 1 nähert sich der Graph beliebig nahe an die negative x-Achse; die negative x-Achse ist Asymptote. }} | + | * Für a > 1 nähert sich der Graph beliebig nahe an die negative x-Achse; die negative x-Achse ist Asymptote. |
| + | |||
| + | '''b ≠ 1''' | ||
| + | * Wenn b > 0 ist, treten nur positive Funktionswerte auf.<br> | ||
| + | * Wenn b < 0 ist, treten nur negative Funktionswerte auf. | ||
| + | |||
| + | * Der Graph geht durch den Punkt (0;b) | ||
| + | |||
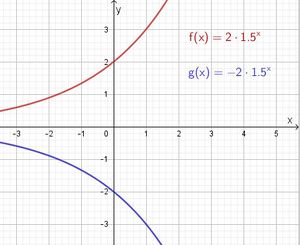
| + | * Die Graphen der Funktionen f mit f(x) = b·a<sup>x</sup> und g mit g(x) = -b ·a<sup>x</sup> sind symmetrisch bezüglich der x-Achse. }} | ||
Version vom 23. Februar 2021, 14:37 Uhr
Inhaltsverzeichnis |
Die Funktion 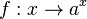
1. Für 0 < a < 1 ist die Exponentialfunktion streng monoton fallend, für a > 1 ist sie streng monoton steigend.
2. Für a = 1 ist die Funktion konstant.
3. Der Graph der Funktion verläuft für alle Werte von a oberhalb der x-Achse.
Die Funktion 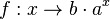
1. Wenn der Faktor b negativ ist, verläuft der Graph der Funktion unterhalb der x-Achse.

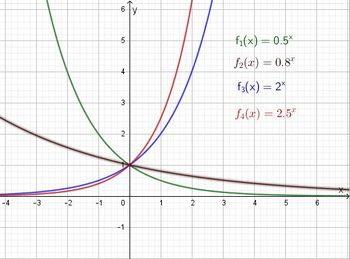
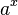 ist stets positiv.
ist stets positiv.
 mit
mit 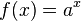 und
und  mit
mit 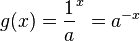 lliegen symmetrisch bezüglich der y-Achse.
lliegen symmetrisch bezüglich der y-Achse.
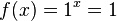 konstant,
konstant,
