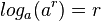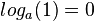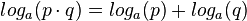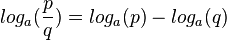M10 Der Logarithmus: Unterschied zwischen den Versionen
Aus RSG-Wiki
(Die Seite wurde neu angelegt: „Die Gleichung <math>2^x = 4</math> ist ganz leicht zu lösen. Man erhält <math> x = 2</math>. Dies geht immer gut, wenn der Wert auf der rechten Seite eine Po…“) |
|||
| Zeile 18: | Zeile 18: | ||
<math>10^x = 5</math> hat die Lösung <math> x = log_{10}(5)</math><br> | <math>10^x = 5</math> hat die Lösung <math> x = log_{10}(5)</math><br> | ||
<math>2^x = 19 </math> hat die Lösung <math>x = log_2[18)</math> | <math>2^x = 19 </math> hat die Lösung <math>x = log_2[18)</math> | ||
| + | |||
| + | {{Merksatz|MERK=Es ist <math>log_a(a^r) = r</math> | ||
| + | |||
| + | <math>log_a(1) = 0</math> | ||
| + | |||
| + | Rechengesetze des Logarithmus | ||
| + | |||
| + | <math>log_a(p\cdot q) = log_a(p) + log_a(q)</math> | ||
| + | |||
| + | <math>log_a(\frac{p}{q})=log_a(p) - log_a(q)</math> | ||
| + | |||
| + | <math>log_a(p^r) = r\cdot log_a(p)</math> }} | ||
Version vom 21. März 2021, 18:21 Uhr
Die Gleichung 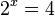 ist ganz leicht zu lösen. Man erhält
ist ganz leicht zu lösen. Man erhält 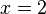 . Dies geht immer gut, wenn der Wert auf der rechten Seite eine Potenz der Basis ist, also
. Dies geht immer gut, wenn der Wert auf der rechten Seite eine Potenz der Basis ist, also
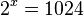 hat die Lösung
hat die Lösung 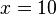 ,
,
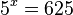 hat die Lösung
hat die Lösung 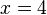 ,
,
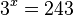 hat die Lösung
hat die Lösung 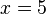 .
.
Doch was macht man, wenn die Gleichung 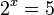 lautet?
lautet?
|
Merke:
Die Gleichung Man spricht für |
Beispiele: 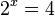 hat die Lösung
hat die Lösung 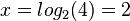
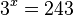 hat die Lösung
hat die Lösung 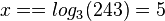
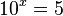 hat die Lösung
hat die Lösung 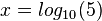
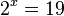 hat die Lösung
hat die Lösung 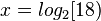
|
Merke:
Es ist
Rechengesetze des Logarithmus
|

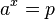 mit a
mit a 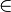 R+ und p > 0 hat die Lösung
R+ und p > 0 hat die Lösung 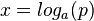 .
.