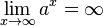M10 Grenzwert und Funktionen: Unterschied zwischen den Versionen
Aus RSG-Wiki
(Die Seite wurde neu angelegt: „=Exponentialfunktionen= {{Merksatz|MERK=Die Exponentialfunktion <math>f: x \rightarrow a^x</math> mit a > 0 gilt: 0 < a < 1: <math>\lim_{x \to -\infty} a^x =…“) |
Version vom 6. Mai 2021, 13:51 Uhr
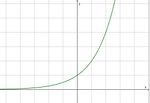
Exponentialfunktionen
|
Merke:
Die Exponentialfunktion |
124/2 Man weiß von Exponentialfunktionen 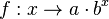 , dass
, dass 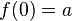 und
und 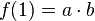 ist. Wenn a = 1 ist, dann ist
ist. Wenn a = 1 ist, dann ist 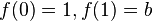 . Damit findet man leicht die Zuordnung Term - Graph.
. Damit findet man leicht die Zuordnung Term - Graph.
A - k
B - f
C - m
D - h
E - g
125/3a) 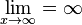 , die Funktion divergiert für
, die Funktion divergiert für 
b) Die Funktion konvergiert für  , es ist
, es ist 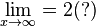
c) Die Funktion konvergiert für  , es ist
, es ist 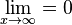
d) Die Funktion konvergiert für  , es ist
, es ist 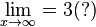
e) Die Funktion divergiert unbestimmt für 


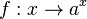 mit a > 0 gilt:
mit a > 0 gilt:
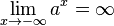 und
und 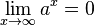

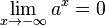 und
und