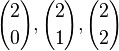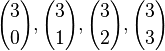M9 Simulation von Zufallsexperimenten: Unterschied zwischen den Versionen
| Zeile 120: | Zeile 120: | ||
<center>{{#ev:youtube |HlNoMh2M1_A|350}}</center> }} | <center>{{#ev:youtube |HlNoMh2M1_A|350}}</center> }} | ||
| − | {{Aufgaben-blau|7|2=Berechne die Wahrscheinlichkeit für 6 | + | {{Aufgaben-blau|7|2=Berechne die Wahrscheinlichkeit für 6 Richtige im Zahlenlotto. }} |
{{Lösung versteckt|1='''6 Richtige'''<br> | {{Lösung versteckt|1='''6 Richtige'''<br> | ||
| − | Wir stellen uns ein Baumdiagramm vor mit den 6 Verzweigungen, wobei jeweils nach links "gezogene Zahl" <math>Z</math> und nach rechts "nicht gezogene Zahl" <math>\overline Z</math> als Äste gehen. Bei der obersten Verzweigung ist die Wahrscheinlichkeit <math>P(Z)=\frac{6}{49}</math> und <math>P(\overline Z)=\frac{43}{49}</math>. Für die vier Ziehungen der ersten vier Kugeln sieht das Baumdiagramm so aus: <br> | + | Wir stellen uns ein vereinfachtes Baumdiagramm vor mit den 6 Verzweigungen, wobei jeweils nach links "gezogene Zahl" <math>Z</math> und nach rechts "nicht gezogene Zahl" <math>\overline Z</math> als Äste gehen. Bei der obersten Verzweigung ist die Wahrscheinlichkeit <math>P(Z)=\frac{6}{49}</math> und <math>P(\overline Z)=\frac{43}{49}</math>. Für die vier Ziehungen der ersten vier Kugeln sieht das Baumdiagramm so aus: <br> |
[[Datei:Lotto 1.jpg]]<br> | [[Datei:Lotto 1.jpg]]<br> | ||
Die Wahrscheinlichkeit für "6 Richtige" ist dann <math>P(6 Richtige)=\frac{6}{49}\cdot \frac{5}{48} \cdot \frac{4}{47}\cdot\frac{3}{46}\cdot \frac{2}{45} \cdot \frac{1}{44}=\frac{6\cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{49\cdot 48 \cdot 47 \cdot 46 \cdot 45\cdot 44} =\frac{1}{13983816}=7,15\cdot 10^{-8}</math> | Die Wahrscheinlichkeit für "6 Richtige" ist dann <math>P(6 Richtige)=\frac{6}{49}\cdot \frac{5}{48} \cdot \frac{4}{47}\cdot\frac{3}{46}\cdot \frac{2}{45} \cdot \frac{1}{44}=\frac{6\cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{49\cdot 48 \cdot 47 \cdot 46 \cdot 45\cdot 44} =\frac{1}{13983816}=7,15\cdot 10^{-8}</math> | ||
| + | }} | ||
| − | |||
| − | |||
| − | |||
| − | }} | + | Im letzten Video wurde eine andere Art der Berechnung dieser Wahrscheinlichkeit gezeigt. Es wird mit Laplace-Wahrscheinlichkeiten <math>P(E)=\frac{Anzahl\ der \ fuer\ E\ guenstigen\ Ergebnisse}{Anzahl\ aller\ Ergebnisse}</math> gearbeitet. Es gibt 49·48·47·46·45·44=10 068 348 752 Möglichkeiten sechs Gewinnzahlen zu ziehen. Bei der Ziehung werden die Kugeln der Reihe nach wie sie gezogen wurden aufgereiht, also etwa 7, 46, 22, 34, 15, 34. Nach der Ziehung werden diese sechs Zahlen der Größe nach mit der Kleinsten beginnend angeordnet. Um sechs Zahlen anzuordnen gibt es 6! = 6·5·4·3·2·1 = 720 Möglichkeiten, die alle zu den gleichen sechs Gewinnzahlen führen. Daher muss man 49·48·47·46·45·44=10 068 348 752 durch 6! = 6·5·4·3·2·1 teilen und hat dann <math>\frac{49\cdot 48 \cdot 47 \cdot 46 \cdot 45\cdot 44}{6\cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}=13983816 </math> Möglichkeiten die sechs Zahlen aus 49 Zahlen zu ziehen. Die Wahrscheinlichkeit für P("6 Richtige")=<math>\frac{1}{13983816}=7,15\cdot 10^{-8}</math>. |
| + | Für den Term <math>\frac{49\cdot 48 \cdot 47 \cdot 46 \cdot 45\cdot 44}{6\cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}</math> führt man eine eigene Bezeichnung ein. Mit Fakultäten lässt sich der Term schreiben: <math>\frac{49\cdot 48 \cdot 47 \cdot 46 \cdot 45\cdot 44}{6\cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}=\frac{49\cdot 48 \cdot 47 \cdot 46 \cdot 45\cdot 44 \cdot 43 \cdot ...\cdot 1}{6\cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 \cdot 43 \cdot ... \cdot 1}=\frac{49!}{6!\cdot 43!}</math>. Und für den letzten Ausdruck <math> | ||
| + | \frac{49!}{6!\cdot 43!}</math> schreibt man <math>{49 \choose 6}</math>. Es ist also <math>\frac{49\cdot 48 \cdot 47 \cdot 46 \cdot 45\cdot 44}{6\cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}=\frac{49!}{6!\cdot 43!}={49 \choose 6}</math>. | ||
{{Merksatz|MERK=n! ist das Produkt der Zahlen von 1 bis n, also n! = 1 ·2 · 3 · ... · (n-1) · n und heißt '''n Fakultät'''. Außerdem ist 0! = 1. | {{Merksatz|MERK=n! ist das Produkt der Zahlen von 1 bis n, also n! = 1 ·2 · 3 · ... · (n-1) · n und heißt '''n Fakultät'''. Außerdem ist 0! = 1. | ||
| − | Der mathematische Term <math>{n \choose k}</math> heißt '''Binomialkoeffizient''' und man berechnet seinen Wert mittels <math>{n \choose k}=\frac{n!}{k!\cdot(n-k)!}</math>, mit <math>k \le n</math>. | + | Der mathematische Term <math>{n \choose k}</math> heißt '''Binomialkoeffizient''' und man berechnet seinen Wert mittels <math>{n \choose k}=\frac{n!}{k!\cdot(n-k)!}</math>, mit <math>k \le n</math>. <br> |
| + | Man spricht für <math>{n \choose k}</math>: "n über k" oder "k aus n". }} | ||
| − | {{Aufgaben-blau| | + | {{Aufgaben-blau|8|2=Berechne a) <math>{2 \choose 0}, {2 \choose 1}, {2 \choose 2}</math> |
b) <math>{3 \choose 0}, {3 \choose 1}, {3 \choose 2}, {3 \choose 3} </math> | b) <math>{3 \choose 0}, {3 \choose 1}, {3 \choose 2}, {3 \choose 3} </math> | ||
c) <math>{49 \choose 6}</math> }} | c) <math>{49 \choose 6}</math> }} | ||
| + | |||
| + | {{Lösung versteckt|1=a) <math>{2 \choose 0}=\frac{2!}{0!\cdot 2!}=\frac{2\cdot 1}{1\cdot 2 \cdot 1}=1</math><br> | ||
| + | <math>{2 \choose 1}=\frac{2!}{1!\cdot 1!}=\frac{2}{1\cdot 1}=2</math><br> | ||
| + | <math>{2 \choose 2}=\frac{2!}{2!\cdot 0!}=\frac{2\cdot 1}{2\cdot 2 \cdot 1}=1</math> | ||
| + | |||
| + | b) <math>{3 \choose 0}=\frac{3!}{0!\cdot 3!}=\frac{3\cdot2\cdot 1}{1\cdot 3 \cdot 2 \cdot 1}=1</math><br> | ||
| + | <math>{3 \choose 1}=\frac{3!}{1!\cdot 2!}=\frac{3\cdot2\cdot 1}{1\cdot 2 \cdot 1}=3</math><br> | ||
| + | <math>{3 \choose 2}=\frac{3!}{2!\cdot 1!}=\frac{3\cdot2\cdot 1}{1\cdot 2 \cdot 1 \cdot 1}=3</math><br> | ||
| + | <math>{3 \choose 3}=\frac{3!}{3!\cdot 0!}=\frac{3\cdot2\cdot 1}{3 \cdot 2 \cdot 1 \cdot 1}=1</math><br> | ||
| + | |||
| + | c) <math>{49 \choose 6}=\frac{49!}{6!\cdot 43!}=\frac{49\cdot 48 \cdot 47\cdot 46\cdot 45 \cdot 44 \cdot 43 \cdot ...3\cdot2\cdot 1}{6\cdot 5\cdot ... \cdot 2 \cdot 1\cdot 43\cdot 42\cdot ... \cdot 2 \cdot 1}=\frac{49\cdot 48 \cdot 47 \cdot 46 \cdot 45\cdot 44}{6\cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}=13983816</math> }} | ||
| + | |||
| + | |||
| + | |||
| + | Mit den Binomialkoeffizienten lassen sich die Wahrscheinlichkeiten P("k Richtige") im Zahlenlotte leicht berechnen. Man betrachtet immer die Anzahl aller Ergebnisse <math>{49 \choose 6}=13983816</math> und muss sich dann nur noch die Anzahl der für E günstigen Ergebnisse überlegen.<br> | ||
| + | Für "6 Richtige" gibt es nur ein günstiges Ergebnis, also ist <math>P(6\ Richtige)=\frac{{6 \choose 6}\cdot{43 \choose 0}}{{49 \choose 6}}=\frac{1}{13983816}=7,15\cdot 10^{-8}</math>. | ||
| + | |||
| + | Für "5 Richtige" hat man <math>{6 \choose 5}=\frac{6!}{1!\cdot 5!}=6</math> Möglichkeiten 5 richtige Kugeln aus den 6 gezogenen Kugeln und <math>{43 \choose 1}=\frac{43!}{1!\cdot 42!}=43</math> Möglichkeiten eine Kugeln aus den 43 nicht gezogenen Kugeln auszuwählen. Also hat man 6·43 = 258 günstige Ergebnisse und die Wahrscheinlichkeit für "5 Richtige" ist <math>P(5\ Richtige)=\frac{{6 \choose 5}\cdot{43 \choose 1}}{{49 \choose 6}}=\frac{6\cdot 43}{13983816}=1,84\cdot 10^{-5}</math>. | ||
| + | |||
| + | Für "4 Richtige" gibt es <math>{6 \choose 4}=\frac{6!}{2!\cdot 4!}=\frac{6\cdot 5\cdot 4\cdot 3\cdot 2 \cdot 1}{2\cdot 1 \cdot 4\cdot 3 \cdot 2 \cdot1}=\frac{6\cdot 5}{2}=15</math> Möglichkeiten aus den 6 gezogenen Zahlen 4 zu nehmen und <math>{43 \choose 2}=\frac{43!}{2!\cdot 41!}=\frac{43\cdot 42\cdot 41\cdot 40\cdot ... \cdot 1}{2\cdot 1 \cdot 41\cdot 40 \cdot ... \cdot1}=\frac{43\cdot 42}{2}=903</math> Möglichkeiten 2 Kugeln aus den 43 nicht gezogenen Kugeln zu wählen. Also hat man 15 · 903 = 13545 günstige Ergebnisse für "4 Richtige". Die Wahrscheinlichkeit für "4 Richtige" ist dann <math>P(4\ Richtige)=\frac{{6 \choose 4}\cdot{43 \choose 2}}{{49 \choose 6}}=\frac{15\cdot 903}{13983816}=9,69\cdot 10^{-4}</math>. | ||
| + | |||
| + | Für "3 Richtige" gibt es <math>{6 \choose 3}=\frac{6!}{3!\cdot 3!}=\frac{6\cdot 5\cdot 4\cdot 3\cdot 2 \cdot 1}{3\cdot 2\cdot 1 \cdot 3 \cdot 2 \cdot1}=\frac{6\cdot 5 \cdot 4}{3\cdot 2}=20</math> Möglichkeiten aus den 6 gezogenen Zahlen 3 zu nehmen und <math>{43 \choose 3}=\frac{43!}{3!\cdot 40!}=\frac{43\cdot 42\cdot 41\cdot 40\cdot 39 \cdot... \cdot 1}{3\cdot 2\cdot 1 \cdot 40 \cdot 29\cdot... \cdot1}=\frac{43\cdot 42 \cdot 41}{3\cdot 2}=12341</math> Möglichkeiten 3 Kugeln aus den 43 nicht gezogenen Kugeln zu wählen. Also hat man 20 · 12341 = 148092 günstige Ergebnisse für "3 Richtige". Die Wahrscheinlichkeit für "3 Richtige" ist dann <math>P(3\ Richtige)=\frac{{6 \choose 3}\cdot{43 \choose 3}}{{49 \choose 6}}=\frac{20\cdot 12341}{13983816}=1,77\cdot 10^{-2}</math>. | ||
| + | |||
| + | |||
| + | Mit dem Baumdiagramm aus Aufgabe 7 hätte man echte Probleme gehabt, diese Wahrscheinlichkeiten zu berechnen. Dazu war es viel zu vereinfacht. | ||
| + | |||
| + | |||
| + | {{Aufgaben-blau|9|2=Mit welcher Wahrscheinlichkeit gewinnt man beim Zahlenlotte 6 aus 49?}} | ||
| + | |||
| + | {{Lösung versteckt|1=Man gewinnt, wenn man mindestens 3 Zahlen richtig getippt hat. Die Wahrscheinlichkeit hierfür ist <math>P(mindestens\ 3\ Richtige) =7,15\cdot 10^{-8}+1,84\cdot 10^{-5}+9,69\cdot 10^{-4}+ 1,77\cdot 10^{-2}=0,018687<2%</math> }} | ||
Version vom 13. Mai 2021, 10:25 Uhr
|
Merke:
Sehr viele Zufallsexperimente können mit dem Urnenmodell simuliert werden. Beim Urnenmodell hat man eine Urne in der verschiedenfarbige, aber ansonsten nicht unterscheidbare Kugeln sind. Ein Experiment mit dem Urnenmodell besteht darin, dass man n-mal "blind" nacheinander eine Kugel zieht und die Farbe notiert. Beim Ziehen mit Zurücklegen ändert sich die der Urneninhalt für den nächsten Zug nicht, beim Ziehen ohne Zurücklegen ändert sich der Urneninhalt für den nächsten Zug . |
150/1a) In einer Urne sind 8 Kugeln jeweils verschiedener Farbe. Man zieht eine Kugel mit Zurücklegen.
b) Ein Laplace-Tetraeder hat 4 Flächen und auf auf jeder Fläche sind in den Ecken Zahlen 1, 2, 3 oder 4. Die Zahl, die oben an der Spitze auf allen drei Seiten angezeigt wird, ist geworfen.
100px
In einer Urne sind 4 verschiedenfarbige Kugeln und man zieht eine Kugel mit Zurücklegen.
c) In einer Urne sind eine weiße und eine schwarze Kugel. Man zieht eine Kugel mit Zurücklegen.
150/2 Ein Laplace-Würfel hat 6 Seiten, die mit den Ziffern 1, 2, 3, 4, 5, 6 beschriftet sind. Von den Zahlen sind 2, 3, 5 Primzahlen und 1, 4, 6 sind keine Primzahlen. Es gibt also 3 Primzahlen und 3 Nicht-Primzahlen. Also ist P("Primzahl") = P("Nicht-Primzahl") = 0,5.
Man nimmt eine Urne in der eine rote und eine schwarze Kugel ist. Zieht man eine rote Kugel, bedeutet das Primzahl, die schwarze Kugel bedeutet Nicht-Primzahl. Man zieht viermal eine Kugel notiert die Farbe und legt die Kugel wieder zurück.
Es ist P("rote Kugel" = P("schwarze Kugel") = 0,5.
Im Buch sind neben der Aufgabe die möglichen 6 Ergebnisse für das Ereignis "genau zwei Augenzahlen sind Primzahlen" abgebildet. Also ist P("genau zwei Augenzahlen sind Primzahlen") = 6·0,54=0,375.
Man kann sich auch überlegen wie viele Fälle es gibt zwei rote Kugeln auf 4 Plätze zu verteilen, indem man systematisch vorne mit zwei roten Kugeln anfängt und dann die rechte rote Kugel nach rechts wandern lässt: rrss, rsrs, rssr, srrs, srsr, ssrr
151/3a) 60% = . Also nimmt man eine Urne mit 3 weißen und 2 schwarzen Kugeln und zieht fünfmal mit Zurücklegen. 3 weiße Kugeln , weil deren Anteil, die dem "Fieber sinkt" entsprechen, in der Urne 60% ist und damit der Anteil der schwarzen Kugeln, die dem Anteil "Fieber sinkt nicht" entsprechen, 40% ist.
. Also nimmt man eine Urne mit 3 weißen und 2 schwarzen Kugeln und zieht fünfmal mit Zurücklegen. 3 weiße Kugeln , weil deren Anteil, die dem "Fieber sinkt" entsprechen, in der Urne 60% ist und damit der Anteil der schwarzen Kugeln, die dem Anteil "Fieber sinkt nicht" entsprechen, 40% ist.
Lucas hat nun die 10 Ergebnisse, dass genau drei weiße Kugeln gezogen werden dargestellt. Dafür gibt es 10 Möglichkeiten.
b) (1) bedeutet, dass genau drei weiße Kugeln gezogen werden. P("genau drei weiße Kugeln")=10·0,6·0,6·0,6·0,4·0,4=0,3456
(2) bedeutet, dass genau zwei weiße Kugeln gezogen werden. P("genau zwei weiße Kugeln")=10·0,6·0,6·0,4·0,4·0,4=0,2304
Es gibt wie in a) gezeigt 10 Möglichkeiten 2 schwarze Kugeln auf 5 Plätze zu verteilen. Dieses Ergebnis kann man hier übernehmen.
(3) bedeutet höchstens zwei weiße Kugeln, also keine weiße Kugel, eine weiße Kugel oder zwei weiße Kugeln.
P("höchstens zwei weiße Kugeln")=P("keine wieße Kugel") + P("eine weiße Kugel") + P("zwei weiße Kugeln") = 0,45 + 5·0,44·0,6 + 10·0,43·0,62 = 0,31744
(4) bedeutet, dass mindestens zwei weiße Kugeln gezogen werden, also zwei, drei, vier oder fünf weiße Kugeln.
151/4
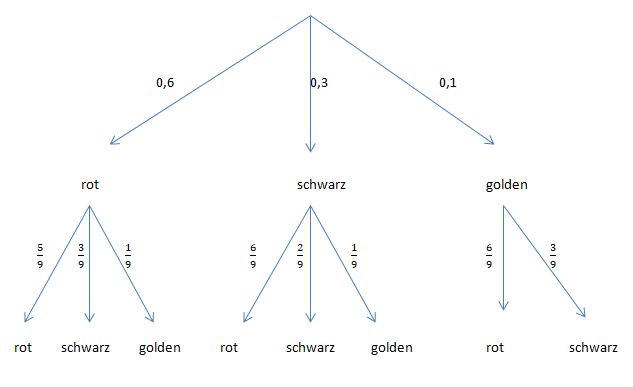
b) (1): P("zwei rote Kugeln") = 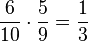
(2): P("nicht die goldene Kugel")=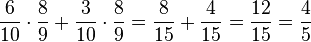
(3): P("zwei gleichfarbige Kugeln")=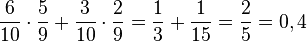
(4): P("goldene und rote Kugel") = P(rg) + P(gr) = 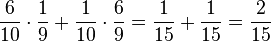
151/5a) Die CD's eines Künstlers entsprechen einer Farbe der Kugeln in der Urne. Man nehme eine Urne mit 15 Kugeln, davon sind 5 rot (Anastacia), drei blau (Mariah Carey), vier grün (DJ Bobo) eine weiß (Madonna) und zwei gelb (Tokoa Hotel).
Sophia zieht zwei Kugeln nacheinander ohne Zurücklegen.
b) Die Aussage Sophies ist richtig!
c) (1) P("zwei rote Kugeln")=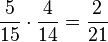
(2) P("eine weiße und eine grüne Kugel") = P(wg) + P(gw)=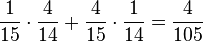
(3) P("keine blaue Kugel") = 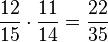
(4) P("höchstens eine gelbe Kugel") = 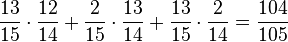
151/6
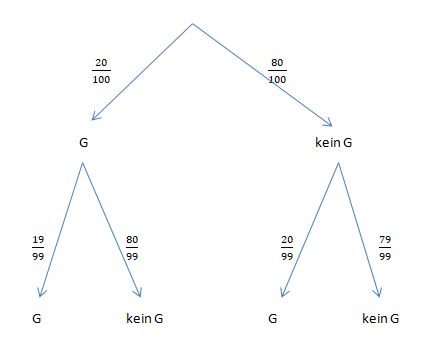
a) P("kein Gewinnlos")=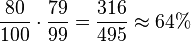
b) P("genau ein Gewinnlos")=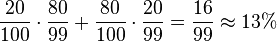
c) P("mindestens ein Gewinnlos") = 1 - P("kein Gewinnlos") =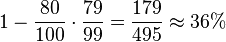
d) P("höchstens ein Gewinnlos") = P("kein Gewinnlos") + P("genau ein Gewinnlos") =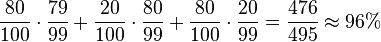
151/7
a) Die 5 Karten liegen auf dem Tisch. Es gibt 5!=120 Möglichkeiten die Karten anzuordnen. Die Anordnung SIMON ist genau eine davon, also ist die Wahrscheinlichkeit 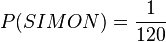
b) 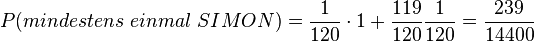
oder über das Gegenereignis 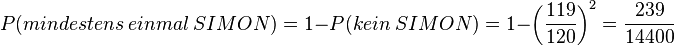
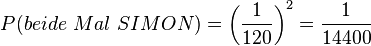
151/8
Aus der Abbildung sieht man P(1) = P(2) = P (0) = 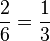
a) P({111}) =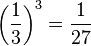
b) P("zweimal 2 und einmal 1") = P({122;212;221}) = 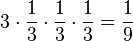
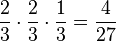
152/10 a)
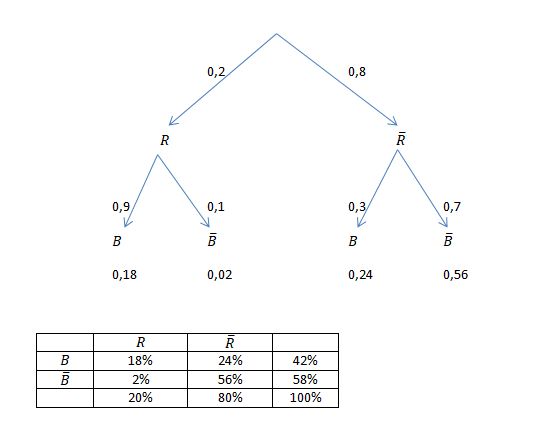
b) Man gerät in den Verdacht Rauschgift mit sich zu führen, wenn der Hund bellt.
Mit dem Baumdiagramm: P(B)=0,18 + 0,24 = 0,42
Mit der Vierfeldertafel: P(B) = 0,42
c) 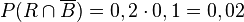
152/11
Man hat eine Urne mit 100 Kugeln, davon sind 12 gelb (dies entspricht 12% Linkshänder) und 88 grün. Man zieht nun nacheinander und ohne Zurücklegen jeweils 1 Kugel und notiert die Farbe. Die Anzahl der gelben Kugeln gibt die Anzahl der Linkshänder wieder.
a) P(mindestens ein Linkshänder) = 1 - P(kein Linkshänder) = 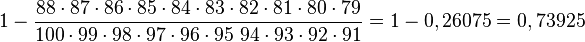
b) P(höchstens ein Linkshänder) = P(kein Linkshänder) + P(genau ein Linkshänder)=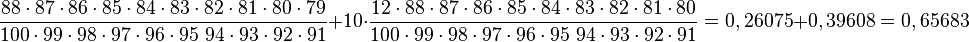
152/12
b) (1) P("beide Senfkrapfen") = 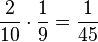
(2) P("genau einen Senfkrapfen") = 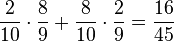
(3) P("keinen Senfkrapfen") = 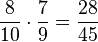
152/13
a) Am Glücksrad ist "rot" mit der Wahrscheinlichkeit p = 0,25 gegeben. Man kann dies mit dem Urnenmodell simulieren, indem man eine Urne mit 4 Kugeln nimmt. Von den Kugeln sind eine rot und drei schwarz. Man zieht nun zehnmal nacheinander jeweils eine Kugel, notiert die Farbe und legt die Kugel zurück.
b) P("Lucas hat genau einmal rot") = 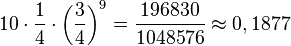
P("keinmal rot") = 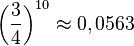
P("höchstens einmal rot") = P("keinmal rot") + P("genau einmal rot") = 0,0563 + 0,1877 = 0,2440
30px Versuch
Hinführung zum Zahlenlotte durch ein einfacheres Spiel "3 aus 20". Und nun zum Zahlenlotte "6 aus 49" |
6 Richtige
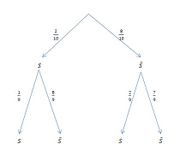
Wir stellen uns ein vereinfachtes Baumdiagramm vor mit den 6 Verzweigungen, wobei jeweils nach links "gezogene Zahl" 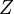 und nach rechts "nicht gezogene Zahl"
und nach rechts "nicht gezogene Zahl" 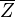 als Äste gehen. Bei der obersten Verzweigung ist die Wahrscheinlichkeit
als Äste gehen. Bei der obersten Verzweigung ist die Wahrscheinlichkeit 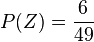 und
und 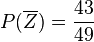 . Für die vier Ziehungen der ersten vier Kugeln sieht das Baumdiagramm so aus:
. Für die vier Ziehungen der ersten vier Kugeln sieht das Baumdiagramm so aus:
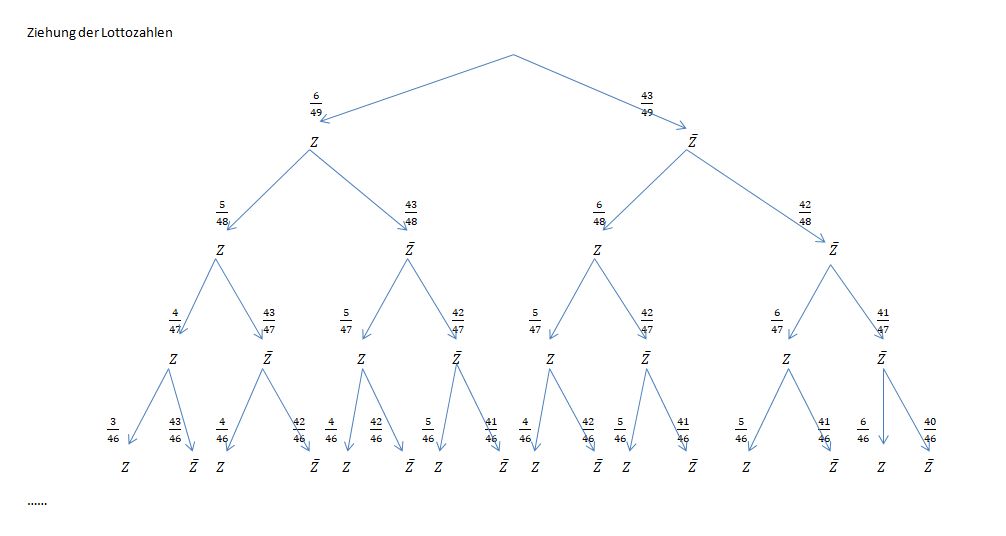
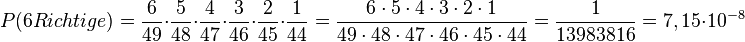
Im letzten Video wurde eine andere Art der Berechnung dieser Wahrscheinlichkeit gezeigt. Es wird mit Laplace-Wahrscheinlichkeiten 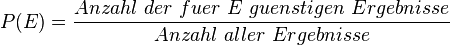 gearbeitet. Es gibt 49·48·47·46·45·44=10 068 348 752 Möglichkeiten sechs Gewinnzahlen zu ziehen. Bei der Ziehung werden die Kugeln der Reihe nach wie sie gezogen wurden aufgereiht, also etwa 7, 46, 22, 34, 15, 34. Nach der Ziehung werden diese sechs Zahlen der Größe nach mit der Kleinsten beginnend angeordnet. Um sechs Zahlen anzuordnen gibt es 6! = 6·5·4·3·2·1 = 720 Möglichkeiten, die alle zu den gleichen sechs Gewinnzahlen führen. Daher muss man 49·48·47·46·45·44=10 068 348 752 durch 6! = 6·5·4·3·2·1 teilen und hat dann
gearbeitet. Es gibt 49·48·47·46·45·44=10 068 348 752 Möglichkeiten sechs Gewinnzahlen zu ziehen. Bei der Ziehung werden die Kugeln der Reihe nach wie sie gezogen wurden aufgereiht, also etwa 7, 46, 22, 34, 15, 34. Nach der Ziehung werden diese sechs Zahlen der Größe nach mit der Kleinsten beginnend angeordnet. Um sechs Zahlen anzuordnen gibt es 6! = 6·5·4·3·2·1 = 720 Möglichkeiten, die alle zu den gleichen sechs Gewinnzahlen führen. Daher muss man 49·48·47·46·45·44=10 068 348 752 durch 6! = 6·5·4·3·2·1 teilen und hat dann 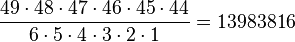 Möglichkeiten die sechs Zahlen aus 49 Zahlen zu ziehen. Die Wahrscheinlichkeit für P("6 Richtige")=
Möglichkeiten die sechs Zahlen aus 49 Zahlen zu ziehen. Die Wahrscheinlichkeit für P("6 Richtige")=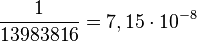 .
.
Für den Term 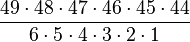 führt man eine eigene Bezeichnung ein. Mit Fakultäten lässt sich der Term schreiben:
führt man eine eigene Bezeichnung ein. Mit Fakultäten lässt sich der Term schreiben: 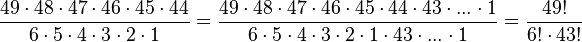 . Und für den letzten Ausdruck
. Und für den letzten Ausdruck 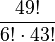 schreibt man
schreibt man 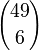 . Es ist also
. Es ist also 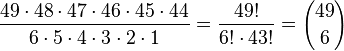 .
.
|
Merke:
n! ist das Produkt der Zahlen von 1 bis n, also n! = 1 ·2 · 3 · ... · (n-1) · n und heißt n Fakultät. Außerdem ist 0! = 1. Der mathematische Term |
a) 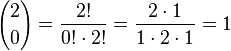
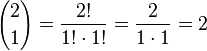
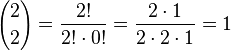
b) 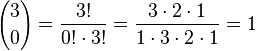
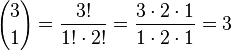
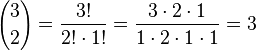
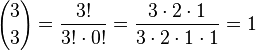
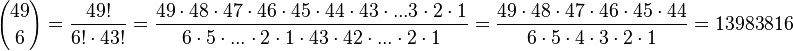
Mit den Binomialkoeffizienten lassen sich die Wahrscheinlichkeiten P("k Richtige") im Zahlenlotte leicht berechnen. Man betrachtet immer die Anzahl aller Ergebnisse 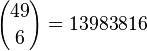 und muss sich dann nur noch die Anzahl der für E günstigen Ergebnisse überlegen.
und muss sich dann nur noch die Anzahl der für E günstigen Ergebnisse überlegen.
Für "6 Richtige" gibt es nur ein günstiges Ergebnis, also ist 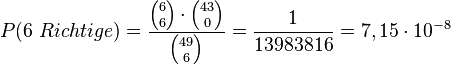 .
.
Für "5 Richtige" hat man 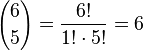 Möglichkeiten 5 richtige Kugeln aus den 6 gezogenen Kugeln und
Möglichkeiten 5 richtige Kugeln aus den 6 gezogenen Kugeln und 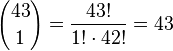 Möglichkeiten eine Kugeln aus den 43 nicht gezogenen Kugeln auszuwählen. Also hat man 6·43 = 258 günstige Ergebnisse und die Wahrscheinlichkeit für "5 Richtige" ist
Möglichkeiten eine Kugeln aus den 43 nicht gezogenen Kugeln auszuwählen. Also hat man 6·43 = 258 günstige Ergebnisse und die Wahrscheinlichkeit für "5 Richtige" ist 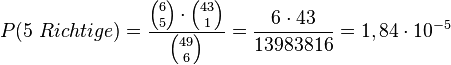 .
.
Für "4 Richtige" gibt es 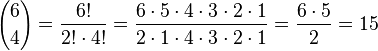 Möglichkeiten aus den 6 gezogenen Zahlen 4 zu nehmen und
Möglichkeiten aus den 6 gezogenen Zahlen 4 zu nehmen und 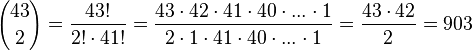 Möglichkeiten 2 Kugeln aus den 43 nicht gezogenen Kugeln zu wählen. Also hat man 15 · 903 = 13545 günstige Ergebnisse für "4 Richtige". Die Wahrscheinlichkeit für "4 Richtige" ist dann
Möglichkeiten 2 Kugeln aus den 43 nicht gezogenen Kugeln zu wählen. Also hat man 15 · 903 = 13545 günstige Ergebnisse für "4 Richtige". Die Wahrscheinlichkeit für "4 Richtige" ist dann 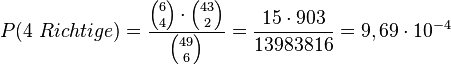 .
.
Für "3 Richtige" gibt es 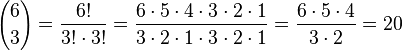 Möglichkeiten aus den 6 gezogenen Zahlen 3 zu nehmen und
Möglichkeiten aus den 6 gezogenen Zahlen 3 zu nehmen und 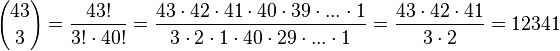 Möglichkeiten 3 Kugeln aus den 43 nicht gezogenen Kugeln zu wählen. Also hat man 20 · 12341 = 148092 günstige Ergebnisse für "3 Richtige". Die Wahrscheinlichkeit für "3 Richtige" ist dann
Möglichkeiten 3 Kugeln aus den 43 nicht gezogenen Kugeln zu wählen. Also hat man 20 · 12341 = 148092 günstige Ergebnisse für "3 Richtige". Die Wahrscheinlichkeit für "3 Richtige" ist dann 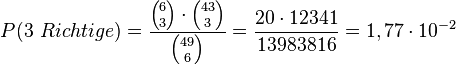 .
.
Mit dem Baumdiagramm aus Aufgabe 7 hätte man echte Probleme gehabt, diese Wahrscheinlichkeiten zu berechnen. Dazu war es viel zu vereinfacht.
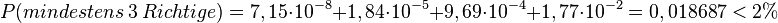

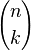 heißt Binomialkoeffizient und man berechnet seinen Wert mittels
heißt Binomialkoeffizient und man berechnet seinen Wert mittels 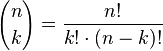 , mit
, mit 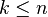 .
.