9b 2021-22: Unterschied zwischen den Versionen
(→Irrationale Zahlen - Quadratwurzel) |
|||
| Zeile 1: | Zeile 1: | ||
| + | __NOCACHE__ | ||
| + | |||
=Mathematik= | =Mathematik= | ||
| Zeile 17: | Zeile 19: | ||
[http://www.matheprisma.uni-wuppertal.de/Module/Geraden/index.htm Geradengleichungen] | [http://www.matheprisma.uni-wuppertal.de/Module/Geraden/index.htm Geradengleichungen] | ||
| + | |||
| + | ==Scheitelform== | ||
| + | |||
| + | Die Funktionsgleichung <math>f(x)=a\cdot (x+d)^2+e</math> ist die Scheitelform einer quadratischen Funktion. <br> | ||
| + | Aus dieser Darstellung kann man leicht die Koordinaten des Scheitels S ablesen, es ist S(-d,e). | ||
| + | <ggb_applet height="700" width="800" | ||
| + | filename="Scheitelform.ggb" /> | ||
| + | |||
| + | Meistens wird der Funktionsterm einer quadratischen Funktion aber als <math>a x^2 + bx + c</math> angegeben. Wie schon bei der pq-Formel kann man diesen Term mittels quadratischer Ergänzung auf die Scheitelform bringen.<br> | ||
| + | 1. Zuerst klammert man a aus den x-Gliedern aus.<br> | ||
| + | Es ist <math>a x^2 + bx + c = a(x^2+\frac{b}{a}x) + c</math><br> | ||
| + | 2. Nun ergänzt man den Term in der Klammer <math>x^2+\frac{b}{a}x</math> mit Hilfe der binomischen Formel zu einem Quadrat. | ||
| + | Es ist <math>x^2+\frac{b}{a}x = x^2+\frac{b}{a}x + (\frac{b}{2a})^2 - (\frac{b}{2a})^2 = (x+\frac{b}{2a})^2 -(\frac{b}{2a})^2</math><br> | ||
| + | 3. Dies verwendet man in dem Term aus 1.<br> | ||
| + | <math>a x^2 + bx + c = a(x^2+\frac{b}{a}x) + c = a[(x+\frac{b}{2a})^2 -(\frac{b}{2a})^2] + c</math><br> | ||
| + | 4. Nun formt man den Term noch so um, dass man die Scheitelform erhält.<br> | ||
| + | Dazu multipliziert man a in die eckige Klammer hinein<br> | ||
| + | <math>a[(x+\frac{b}{2a})^2 -(\frac{b}{2a})^2] + c = a(x+\frac{b}{2a})^2 -a(\frac{b}{2a})^2 + c=a(x+\frac{b}{2a})^2 -a\cdot\frac{b^2}{4a^2} + c = a(x+\frac{b}{2a})^2 -\frac{b^2}{4a} + c </math><br> | ||
| + | Dies ist die Scheitelform und man kann die Scheitelkoordinaten ablesen: <math>S(-\frac{b}{2a};-\frac{b^2}{4a} + c)</math>. | ||
Version vom 19. Dezember 2021, 07:21 Uhr
Inhaltsverzeichnis |
Mathematik
Grundwissen: 5. Klasse, 6. Klasse, 7. Klasse, 8. Klasse, 9. Klasse
Irrationale Zahlen - Quadratwurzel
Zum Beweis der Irrationalität von Wurzel 2
Wiederholung
Ein Einstieg zum Funktionsbegriff
Scheitelform
Die Funktionsgleichung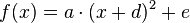 
ist die Scheitelform einer quadratischen Funktion.
Aus dieser Darstellung kann man leicht die Koordinaten des Scheitels S ablesen, es ist S(-d,e).
Meistens wird der Funktionsterm einer quadratischen Funktion aber als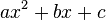 
angegeben. Wie schon bei der pq-Formel kann man diesen Term mittels quadratischer Ergänzung auf die Scheitelform bringen.
1. Zuerst klammert man a aus den x-Gliedern aus.
Es ist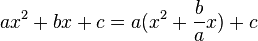 
2. Nun ergänzt man den Term in der Klammer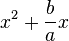 
mit Hilfe der binomischen Formel zu einem Quadrat.
Es ist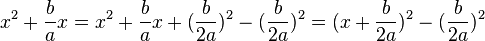 
3. Dies verwendet man in dem Term aus 1.
![a x^2 + bx + c = a(x^2+\frac{b}{a}x) + c = a[(x+\frac{b}{2a})^2 -(\frac{b}{2a})^2] + c](/images/math/9/2/5/925ab32c32aa9d72ddf917e0625996f2.png)
4. Nun formt man den Term noch so um, dass man die Scheitelform erhält.
Dazu multipliziert man a in die eckige Klammer hinein
![a[(x+\frac{b}{2a})^2 -(\frac{b}{2a})^2] + c = a(x+\frac{b}{2a})^2 -a(\frac{b}{2a})^2 + c=a(x+\frac{b}{2a})^2 -a\cdot\frac{b^2}{4a^2} + c = a(x+\frac{b}{2a})^2 -\frac{b^2}{4a} + c](/images/math/f/0/f/f0fc943f34d1fb58df7911c54aa8aad2.png)
Dies ist die Scheitelform und man kann die Scheitelkoordinaten ablesen: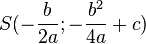 
.
