|
|
| Zeile 27: |
Zeile 27: |
| | | | |
| | {{Lösung versteckt|1=1. A(1;1) und B(9;1) <br> | | {{Lösung versteckt|1=1. A(1;1) und B(9;1) <br> |
| − | 2a) außerhalb des Kreises ist 0<sup>o</sup> < <math>0\gamma</math> < 90<sup>o</sup><br> | + | 2a) Außerhalb des Kreises ist 0<sup>o</sup> < <math>\gamma</math> < 90<sup>o</sup>.<br> |
| − | b) es ist <math>0\gamma</math> = 90<sup>o</sup><br> | + | b) Ist C auf der Kreislinie, so ist <math>0\gamma</math> = 90<sup>o</sup>.<br> |
| − | c) innerhalb des Kreises ist 90<sup>o</sup> < <math>0\gamma</math> < 180<sup>o</sup><br> }} | + | c) Innerhalb des Kreises ist 90<sup>o</sup> < <math>\gamma</math> < 180<sup>o</sup>.<br> }} |
| | | | |
| | {{Merksatz|MERK=Der Satz des Thales | | {{Merksatz|MERK=Der Satz des Thales |
Version vom 3. Juli 2023, 08:00 Uhr
Mathematik
Lehrplan
Binomische Formeln
Konstruktion von Dreiecken mit GeoGebra
Wiederhole die Konstruktioenn von Dreiecken mit den 4 Kongruenzsätzen auf dieser Seite und mache zu jedem Satz die vorgegebene Konstruktion.
Der Satz des Thales
1. Konstruiere in GeoGebra einen Kreis k(M,r) mit M(5;1) und r = 4.
Welche Koordinaten haben die Endpunkte A und B des Durchmessers, der parallel zur x-Achse verläuft?
2. Nimm einen dritten Punkt C und zeichne das Dreieck ABC. Zeichne und miss bei C den Winkel 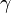 .
.
Bewege nun den Punkt C
a) außerhalb des Kreises
b) auf der Kreislinie
c) innerhalb des Kreises.
Was stellst du für den Winkel 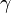 fest?
fest?
3. Bearbeite die 5 Arbeitsblätter auf dieser Seite.
4. Formuliere dein Ergebnis
[Lösung anzeigen][Lösung ausblenden]
1. A(1;1) und B(9;1)
2a) Außerhalb des Kreises ist 0o < 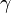 < 90o.
< 90o.
b) Ist C auf der Kreislinie, so ist 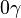 = 90o.
= 90o.
c) Innerhalb des Kreises ist 90
o <
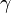
< 180
o.
|
Merke:
Der Satz des Thales
Liegt der Eckpunkt C auf dem Halbkreis über der Seite 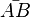 , dann hat das Dreieck ABC bei C einen rechten Winkel ( , dann hat das Dreieck ABC bei C einen rechten Winkel (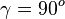 ). ).
Datei:01 Satz des Thales.gif
|
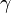 < 90o.
< 90o.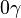 = 90o.
= 90o.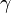 < 180o.
< 180o.
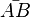 , dann hat das Dreieck ABC bei C einen rechten Winkel (
, dann hat das Dreieck ABC bei C einen rechten Winkel (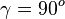 ).
).

