9d 2011-12: Unterschied zwischen den Versionen
Berny1 (Diskussion | Beiträge) (→CSI Rothenburg - Dem Täter auf der Spur) |
Berny1 (Diskussion | Beiträge) (→CSI Rothenburg - Dem Täter auf der Spur) |
||
| Zeile 74: | Zeile 74: | ||
*[http://wiki.zum.de/Ber%C3%BChrungsprobleme_bei_quadratischen_Funktionen Tangenten an quadratische Funktionen und weitere Beispiele] | *[http://wiki.zum.de/Ber%C3%BChrungsprobleme_bei_quadratischen_Funktionen Tangenten an quadratische Funktionen und weitere Beispiele] | ||
| + | |||
| + | <table cellpadding="2" cellspacing="2" border="0" | ||
| + | style="text-align: left; width: 100%;"> | ||
| + | <tr> | ||
| + | <td style="vertical-align: top; background-color: rgb(51, 102, 255); width: 1%;"><br> | ||
| + | </td> | ||
| + | <td style="vertical-align: top;"> | ||
| + | '''Arbeitsaufgaben:''' | ||
====='''CSI Rothenburg - Dem Täter auf der Spur'''===== | ====='''CSI Rothenburg - Dem Täter auf der Spur'''===== | ||
| Zeile 84: | Zeile 92: | ||
2. In Australien wird das Känguru Skippy verdächtigt einen Meter hohen Zaun übersprungen zu haben und das dahinter gelegene Grundstück verwüstet zu haben. Nachdem Detective Scheitel, der wie in solchen Fällen immer hinzugezogen wird, recherchiert hat, dass Kängurus bis zu 30 m weit springen können und eine "Flugbahn" mit der Gleichung y = 1/20(x-30)x vom Absprungort x = 0 zurücklegen schließt er Skippy als Täter aus. Stimmt seine Folgerung? | 2. In Australien wird das Känguru Skippy verdächtigt einen Meter hohen Zaun übersprungen zu haben und das dahinter gelegene Grundstück verwüstet zu haben. Nachdem Detective Scheitel, der wie in solchen Fällen immer hinzugezogen wird, recherchiert hat, dass Kängurus bis zu 30 m weit springen können und eine "Flugbahn" mit der Gleichung y = 1/20(x-30)x vom Absprungort x = 0 zurücklegen schließt er Skippy als Täter aus. Stimmt seine Folgerung? | ||
| + | |||
| + | <br> | ||
| + | |||
| + | <br> | ||
| + | |||
| + | </table> | ||
| + | |||
| + | Lösung: wird noch eingefügt. | ||
Aktuelle Version vom 19. Dezember 2011, 07:44 Uhr
Inhaltsverzeichnis |
Mathematik
Rechnen mit irrationalen Zahlen
Satzgruppe des Pyathagoras
Parabeln und quadratische Gleichungen
Parabeln
Die Funktionen 2. Grades - Parabeln
Übungen:
Überprüfe an dem Geogebraapplet, ob folgende Aussagen wahr oder falsch sind:
- Der Parameter a beeinflusst die Form der Parabel
- Der Parameter c verschiebt den Scheitel in x-Richtung
- Der Parameter b verschiebt den Scheitel in y-Richtung und y-Richtung
Die Scheitelform der Parabel
Übungen zur Scheitelform
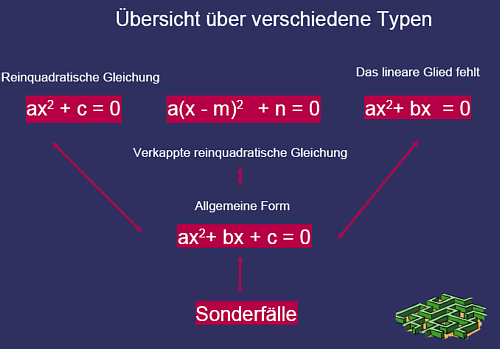
Quadratische Gleichungen
Lösungsstrategien

Anwendung quadratischer Gleichungen auf Funktionen
Nullstellen quadratischer Funktionen
Schnitt von Parabeln mit Parabeln bzw. Geraden
Die Diskriminante
In der ´Mitternachtsformel´
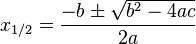
nennt man den Term
D:=Fehler beim Parsen(Syntaxfehler): sqrt{b^2-4ac}}
die Diskriminante, da sie über die Anzahl der Lösungen einer quadratischen Gleichung entscheidet.
Anwendungen
|
Arbeitsaufgaben: CSI Rothenburg - Dem Täter auf der SpurArbeitsaufgaben: 1. Chiefinspector Math hat einen mysteriösen Fall zu lösen. Der Täter kreuzte die x-Achse bei -5 und + 1. 2. In Australien wird das Känguru Skippy verdächtigt einen Meter hohen Zaun übersprungen zu haben und das dahinter gelegene Grundstück verwüstet zu haben. Nachdem Detective Scheitel, der wie in solchen Fällen immer hinzugezogen wird, recherchiert hat, dass Kängurus bis zu 30 m weit springen können und eine "Flugbahn" mit der Gleichung y = 1/20(x-30)x vom Absprungort x = 0 zurücklegen schließt er Skippy als Täter aus. Stimmt seine Folgerung?
|
Lösung: wird noch eingefügt.
Und noch weitere Übungen
|
Quadratische Gleichungen |
|
|
|
Quadratische Funktionen |
|
Parabelgleichungen aufstellen - zuordnen
Scheitel bestimmen
Anwendungen Extremwertaufgaben
Tangenten an Parabeln
|