M8 - Beispiele weiterer gebrochen-rationaler Funktionen: Unterschied zwischen den Versionen
Aus RSG-Wiki
(Die Seite wurde neu angelegt: „Du hast schon verschiedene Graphen gebrochen-rationaler Funktionen gesehen. Hier sollen nun weitere Beispiele gezeigt werden um zu sehen, was alles vorkommen k…“) |
Version vom 24. März 2020, 09:01 Uhr
Du hast schon verschiedene Graphen gebrochen-rationaler Funktionen gesehen. Hier sollen nun weitere Beispiele gezeigt werden um zu sehen, was alles vorkommen kann.
Im folgenden Beispiel stehen in Zähler und Nenner Terme mit x, der Zählerterm ist eine x-Potenz. Man kann den Exponenten der Zählerpotenz ändern und man sieht die Auswirkungen auf den Graphen und die Asymptoten.
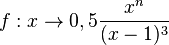für n = 1, 2, 3, 4. In dem Applet kann man mit dem Schieberegler den Exponenten von x im Zählerpolynom ändern.
waagrechte Asymptote. 
