Die Tacoma-Narrows-Brücke: Unterschied zwischen den Versionen
(→Was ist Resonanz) |
(→Was ist Resonanz) |
||
| Zeile 1: | Zeile 1: | ||
=Was ist Resonanz= | =Was ist Resonanz= | ||
| − | Anregung und Resonanz beim Federpendel: {{#ev:youtube |FvtwYwTRJq0|350}} | + | {{Aufgaben-blau||2=Schaue dir dieses Video an:<br> |
| + | Anregung und Resonanz beim Federpendel: {{#ev:youtube |FvtwYwTRJq0|350}}<br> | ||
| + | Beschreibe und erkläre den Versuch. }} | ||
| + | |||
| + | {{Lösung versteckt|Ein Federpendel wird durch einen Exzenter zu Schwingungen angeregt. Der Exzenter dreht sich mit der Winkelgeschwindigkeit <math>\omega</math>, welche variiert werden kann, und hat die Erregerfrequenz <math>f</math>. Ist <math>\omega</math> klein, so schwingt das Federpendel mit der Erregerfrequenz <math>f (\omega = 2\pi f)</math>, seine Amplitude ist klein. Exzenter und Federpendel sind synchron. <br> | ||
| + | Wird <math>\omega</math> des Exzenters gesteigert, dann nimmt die Ampltude des Federpendels zu. Stimmt die Erregerfrequenz <math>f</math> mit der Eigenfrequenz <math> f_0</math> des Federpendels überein, dann hat das Federpendel eine gewaltige Amplitude und die Schwingung erfolgt um <math>\frac{\pi}{2}</math> phasenverschoben. <br> | ||
| + | Steigert man die Erregerfrequenz weiter dann nimmt die Amplitude ab und die Erregerschwingung und Federschwingung sind gegenphasig (Phasenverschiebung <math>\pi</math>. | ||
| + | }} | ||
| + | |||
Resonanz kann man beim [https://www.leifiphysik.de/mechanik/kopplung-von-schwingungen/versuche/resonanz-am-federpendel Federpendel] gut beobachten. Eine schöne [https://www.leifiphysik.de/mechanik/kopplung-von-schwingungen/versuche/erzwungene-schwingung-eines-federpendels-simulation Simulation zur Erregung eines Federpendels]. | Resonanz kann man beim [https://www.leifiphysik.de/mechanik/kopplung-von-schwingungen/versuche/resonanz-am-federpendel Federpendel] gut beobachten. Eine schöne [https://www.leifiphysik.de/mechanik/kopplung-von-schwingungen/versuche/erzwungene-schwingung-eines-federpendels-simulation Simulation zur Erregung eines Federpendels]. | ||
Version vom 7. April 2020, 10:54 Uhr
Was ist Resonanz
Ein Federpendel wird durch einen Exzenter zu Schwingungen angeregt. Der Exzenter dreht sich mit der Winkelgeschwindigkeit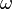 
, welche variiert werden kann, und hat die Erregerfrequenz 
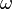. Ist klein, so schwingt das Federpendel mit der Erregerfrequenz 
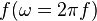, seine Amplitude ist klein. Exzenter und Federpendel sind synchron.
Wird 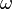des Exzenters gesteigert, dann nimmt die Ampltude des Federpendels zu. Stimmt die Erregerfrequenz mit der Eigenfrequenz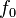 
des Federpendels überein, dann hat das Federpendel eine gewaltige Amplitude und die Schwingung erfolgt um 
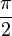phasenverschoben.
Steigert man die Erregerfrequenz weiter dann nimmt die Amplitude ab und die Erregerschwingung und Federschwingung sind gegenphasig (Phasenverschiebung 
.
Resonanz kann man beim Federpendel gut beobachten. Eine schöne Simulation zur Erregung eines Federpendels.
Auf dieser Seite ist erklärt, was man unter Resonanz versteht.
Bearbeite dieses Arbeitsblatt mit dem Applet.
Die Tacoma-Narrows-Brücke
Die erste Tacoma-Narrows-Brücke wurde durch eine Resonanzerscheinung berühmt, durch die sie dann leider auch zerstört wurde. Eine ausführliche Information zur Brücke findet man bei Wikipedia.
Die Brücke war mit einer Mittelspannweite von 853 Metern zum Zeitpunkt ihrer Fertigstellung die drittgrößte Hängebrücke der Welt. Sie wurde am 1. Juli 1940 eröffnet.
Bei Brücken dieser Art war bekannt, dass sich entlang der Brücke Transversalwellen ausbilden können. Schon durch leichten Wind wurde die Brücke zu Eigenschwingungen angeregt und geriet in Resonanz. Daher auch der Beiname "Galloping Gertie".
Würde man mit dem Auto über diese Brücke fahren wollen?
Diese angeregte Querschwingung trug aber nicht zur Zerstörung der Brücke bei, sondern die Brücke stürzte am 7. November 1940 durch eine unerwartet aufgetretene Torsionsschwingung ein.
Zerstörerisch wirkte allerdings die Torsionsschwingung
Erklärung
Im Video von SimplePhysics wird der Einsturz erklärt.
Der Einsturz der Brücke ist auf dieser Seite gut erklärt.
