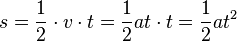Ph9 tx- und tv- Abhängigkeiten
Ihr habt schon zwei Arten von Bewegungen kennengelernt:
- Bewegung mit konstanter Geschwindigkeit und
- Bewegung mit konstanter Beschleunigung
Für beide Bewegungen sammeln wir zuerst unsere bisherigen Kenntnisse:
1. Gleichförmige Bewegung:
30px Merke
Bei einer gleichförmigen Bewegung bewegt sich ein Körper geradlinig mit konstanter Geschwindigkeit v = konstant. 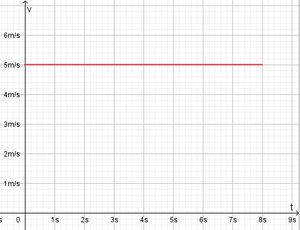 Im ts-Diagramm wird auch nach rechts die Zeit t aber nach oben der zurückgelegte Weg s aufgetragen. 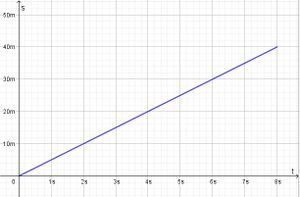 Die Strecke beginnt im Ursprung und steigt linear an. Formeln:
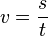 |
Die Fläche unter der Kurve im tv-Diagramm ist eine Rechtecksfläche und berechnet sich als v·t.
Sie stellt den zurückgelegten Weg s dar.
a) Die Bewegung verläuft für 0s ≤ t ≤ 8s ab.
v = 5 m/s
Der insgesamt zurückgelegte Weg ist s = 40m.
2. Gleichmäßig beschleunigte Bewegung:
30px Merke
Bei einer gleichmäßig beschleunigten Bewegung bewegt sich ein Körper geradlinig und wird mit konstanter Beschleunigung beschleunigt. 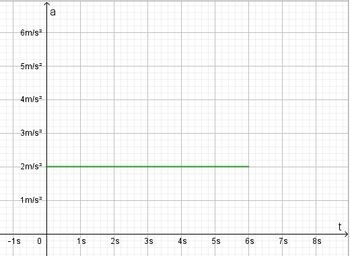 Im tv-Diagramm wird nach rechts die Zeit t und nach oben die Geschwindigkeit v aufgetragen. 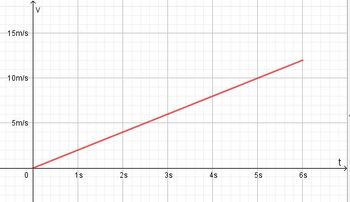 Beschleunigung 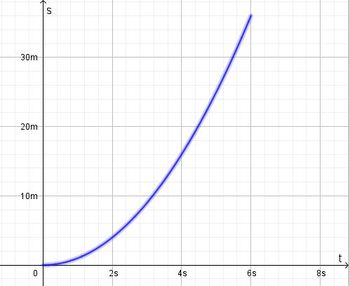 Auch hier stellt die Fläche unter dem Graph im tv-Diagramm den zurückgelegtn Weg s dar. Es ist Formeln:
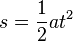 |
a) Die Bewegung verläuft für 0s ≤ t ≤ 6s ab.
a=2m/s²
Die mach 6s erreichte Geschwindigkeit ist v = 12 m/s
Der insgesamt zurückgelegte Weg ist s = 36m.
Beachte: Die Bewegungsgleichung s = v·t darf man nicht bei der Bewegung mit konstanter Beschleunigung verwenden!
61/3 Es handelt sich um Bewegungen mit konstanter Geschwindigkeit. Im ts-Diagramm sind das Geraden. Die Geschwindigkeit gibt die Steigung der Geraden an. Je steiler die Gerade, desto größer ist die Geschwindigkeit.
a) Zeit bergab ist genauso lang wie Zeit bergauf (t-Achse), bergab steiler als bergauf --> Diagramm III
b) Strecke bergauf ist genauso lang wie Strecke bergab (s-Achse), bergauf nicht so steil wie bergab ---> Diagramm II
c) Zeit bergauf ist genauso lang wie Zeit bergab (t-Achse), bergauf nicht so steil wie bergab ---> Diagramm IV
d) Strecke bergab ist genauso lang wie Strecke bergauf (s-Achse), bergab steiler als bergauf ---> Diagramm I
61/4
Bei a) und c) jeweils gleiche Zeiten, bei b) und d) gleiche Strecken!
Man kann nicht gleichzeitig an zwei verschiedenen Orten sein.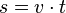
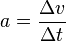 , da a konstant ist gilt auch
, da a konstant ist gilt auch 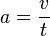 .
.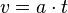 .
.