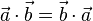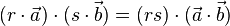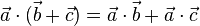M11 Skalarprodukt
In Physik hat man gelernt, dass Arbeit W das Produkt aus der Kraft F, die in Wegrichtung entlang des Weges s wirkt. Man schreibt dann W = F·s. Was macht man aber, wenn man einen Leiterwagen zieht?
350px
Nach unserer Arbeitsdefinition muss man den Wagen so wie er abgebildet ist nach vorne ziehen. Dazu muss man sich bücken und es ist sehr unbequem. Man wird den Handgriff hochnehmen, aber dann wirkt die Kraft nicht mehr in Wegrichtung sondern ist schräg dazu. Wie macht sich das dann in der Arbeit bemerktbar?
Man löst das, indem man die Kraftkomponente Fs in Wegrichtung betrachtet und damit die Arbeit Arbeit W = Fs·s berechnet.
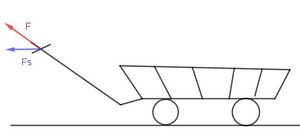
Fs ist die senkrechte Projektion von F auf die Fahrtrichtung.
In der Mathematik führt man hierzu das Skalarprodukt ein, dies wird dann in der Physik auch verwendet und man sagt dann, dass die Arbeit W das Skalarprodukt des Kraftvektors 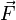 mit dem Wegvektor
mit dem Wegvektor 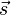 ist, also
ist, also 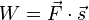 oder ohne Vektoren
oder ohne Vektoren 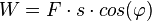 .
.
|
Merke:
Für die Vektoren Das Ergebnis des Skalarprodukts Es ist weiterhin, wenn |
Eine Herleitung der letzten Formel finden Sie im Buch auf Seite 109 oben.
Beispiele:
1. 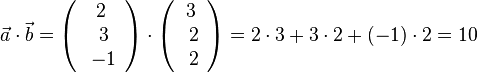 .
.
2. 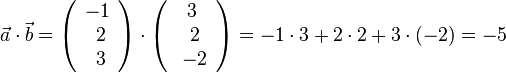 .
.
|
Merke:
Dies führt zur Definition des Winkels. Der Winkel 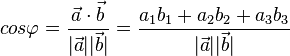
|
Beispiele:
1. 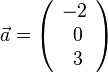 ,
, 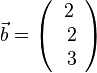 . Es ist
. Es ist 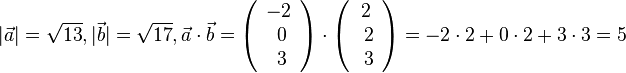 .
.
Damit ist 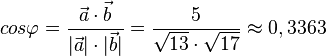 , also
, also 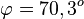
2. 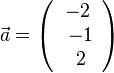 ,
, 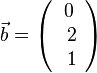 . Es ist
. Es ist 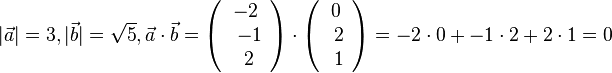 .
.
Damit ist 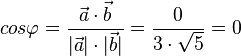 , also
, also 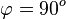 .
.
30px Merke
Haben die zwei Vektoren Ist insbesondere
Dies giilt auch umgekehrt. Ist das Skalarprodukt |
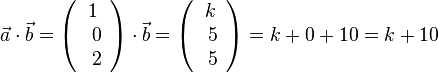 . Es ist k+10 = 0 für k = -10.
. Es ist k+10 = 0 für k = -10.
2. Die drei Einheitsvektoren sind 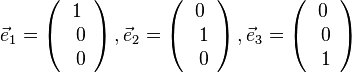 .
.
Es ist 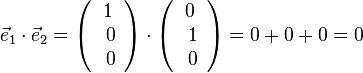 ,
,
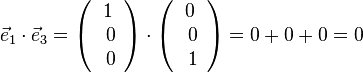 ,
,
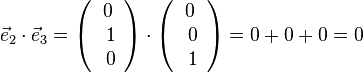
Also sind  paarweise senkrecht zueinander.
paarweise senkrecht zueinander.
3. Es muss sein: 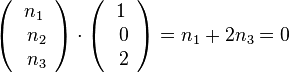 und
und 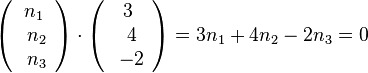
Man hat also zwei Gleichungen 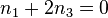 und
und 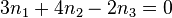 .
.
Löst man die erste Gleichung nach 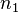 auf, so ist
auf, so ist 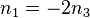 . Dies setzt man in die zweite Gleichung ein und erhält
. Dies setzt man in die zweite Gleichung ein und erhält 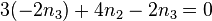 .
.
Dies führt zu der Gleichung 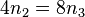 .
.
Wählt man 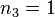 , dann ist
, dann ist 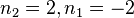 und man hat den Vektor
und man hat den Vektor 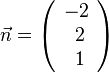 .
.
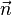 steht senkrecht zu den Vektoren
steht senkrecht zu den Vektoren  .
.
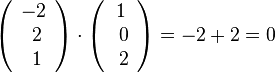 und
und 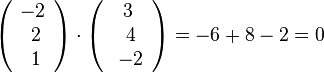
30px Merke
Rechengesetze für das Skalarprodukt Für Vektoren
Auch hier kann man also wie gewohnt rechnen! |

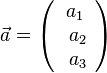 imd
imd 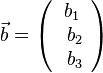 definiert man das Skalarprodukt
definiert man das Skalarprodukt 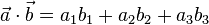 .
.
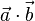 ist eine Zahl (ein Skalar). Es ist
ist eine Zahl (ein Skalar). Es ist 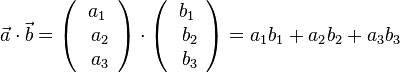 .
.
 der Winkel zwischen den Vektoren
der Winkel zwischen den Vektoren  und
und 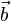 ist
ist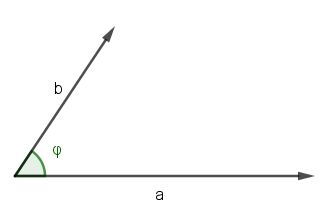
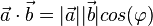
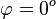 und
und 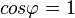 . Dann ist
. Dann ist 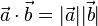 .
.
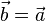 , dann ist
, dann ist 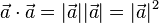 .
. 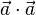 gleich dem Quadrat des Betrags des Vektors
gleich dem Quadrat des Betrags des Vektors 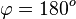 und
und 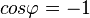 . Dann ist
. Dann ist 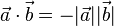 .
.
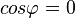 . Damit ist
. Damit ist  .
.
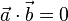 , dann stehen die Vektoren
, dann stehen die Vektoren 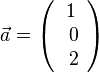 und
und 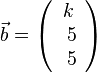 senkrecht zueiander sind.
senkrecht zueiander sind.
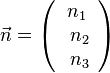 , der senkrecht auf den zwei Vektoren
, der senkrecht auf den zwei Vektoren 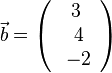 steht.
steht.
 und reelle Zahlen r,s gilt:
und reelle Zahlen r,s gilt: