M11 Verkettung von Funktionen
Die Funktion 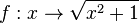 ist eine in ganz R definierte Funktion.
ist eine in ganz R definierte Funktion.
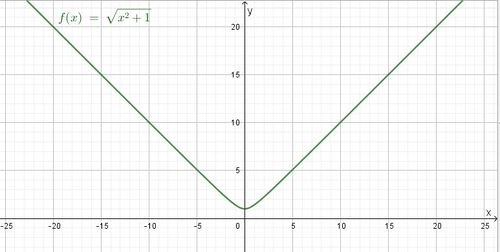
Am Graph sieht man, dass im Punkt (0;1) eine waagrechte Tangente y = 1 vorhanden ist.
Doch wie soll man 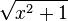 ableitgen?
ableitgen?
Dazu müssen wir die Verknüpfung zweier Funktionen um die Verkettung erweitern. Bisher kennen wir als Verknüpfung zweier Funktiongen f und g
- die Summe f + g
- die Differenz f - g
- die Multiplikation f · g und
- die Division
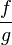
Nun kommt noch die Verkettung 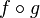 dazu.
dazu.
|
Merke:
Bei der Verkettung (Hintereinanderausführung) |
Für unser Beispiel 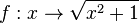 betrachten wir die Funktionen
betrachten wir die Funktionen 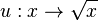 und
und 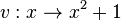 . Es ist
. Es ist 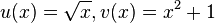 .
.
Setzt man nun 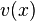 an die Stelle von
an die Stelle von 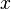 in der Funktion
in der Funktion  , dann hat man
, dann hat man 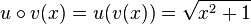 und
und  ist die Verkettung
ist die Verkettung 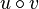 der Funktionen
der Funktionen  und
und  , also
, also 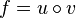 .
.
|
Merke:
Bei der Verkettung |
Beispiele: 1. Für die Funktionen  mit
mit 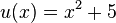 und
und  mit
mit 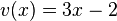 ist
ist
-
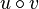 durch
durch 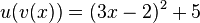 gegeben. (In der Funktion u ersetzt man x durch den Term von v(x).)
gegeben. (In der Funktion u ersetzt man x durch den Term von v(x).)
-
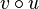 durch
durch 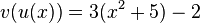 . (In der Funktion v ersetzt man x durch den Term von u(x).)
. (In der Funktion v ersetzt man x durch den Term von u(x).)
Natürlich vereinfacht man noch die Terme. Es ist dann 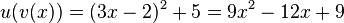 und
und 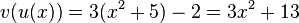 .
.
Insbesondere sieht man, dass die Verkettung nicht kommutativ ist. 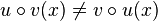 .
.
2. Für die Funktionen  mit
mit 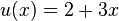 und
und  mit
mit 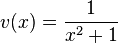 ist
ist
-
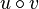 durch
durch 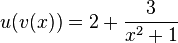 gegeben. (In der Funktion u ersetzt man x durch den Term von v(x).)
gegeben. (In der Funktion u ersetzt man x durch den Term von v(x).)
-
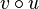 durch
durch 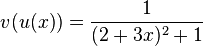 . (In der Funktion v ersetzt man x durch den Term von u(x).)
. (In der Funktion v ersetzt man x durch den Term von u(x).)
3. Für die Funktionen  mit
mit 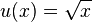 und
und  mit
mit 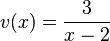 ist
ist
-
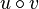 durch
durch 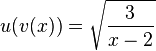 gegeben.
gegeben.
-
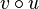 durch
durch 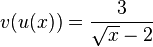 .
.
{{Lösung versteckt|1=a) 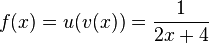 und
und 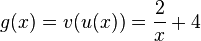
b) ![f(x) = u(v(x))=cos[(x+1)^2]](/images/math/b/e/4/be44141b323c7b684584573c60714290.png) und
und 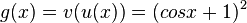
c) 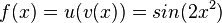 und
und ![g(x)=v(u(x))=[sin(2x)]^2](/images/math/6/5/a/65a43ed2da1cd7ac46565340695f3048.png)
d) 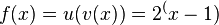 und
und 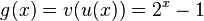
e) 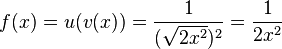 und
und 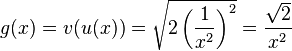
f) 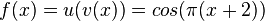 und
und 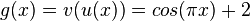
g) 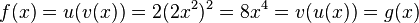
h) 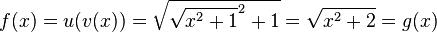

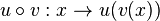 .
.
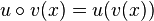 gegeben ist, heißt
gegeben ist, heißt 
