Ph9 Zerfallsgesetz
|
Merke:
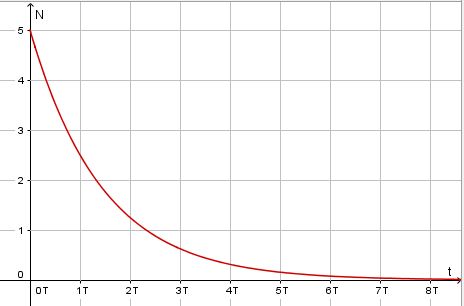
In einem bestimmten Zeitraum Wann ein bestimmter Kern zerfällt, kann nicht vorhergesagt werden, er zerfällt zufällig. Man weiß nur, dass bei einer sehr großen Anzahl von radioaktiven Kernen nach Die Aktivität A eines radioaktiven Stoffes ist die Anzahl der Kernzerfälle pro Zeitintervall. Es ist |
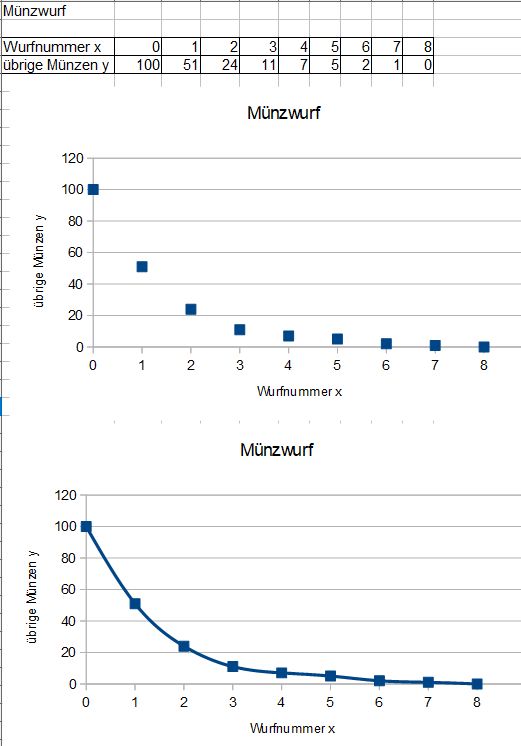
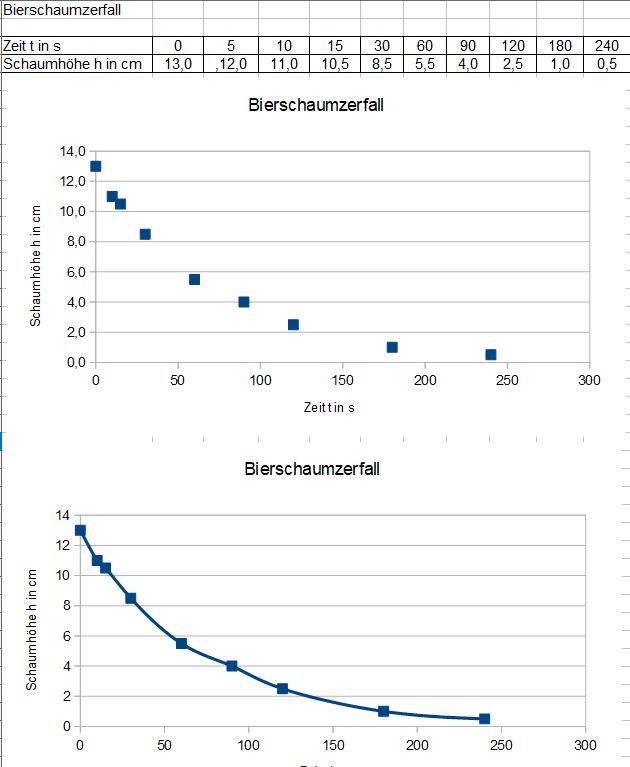
Der Münzwurf und der Bierschaumzerfall sind Analogien zum radioaktiven Zerfall. Beide Zerfälle sind zufällig. Beim Münzwurf kann man nicht vorhersagen, welche Münze nach dem Wurf die "1" zeigt, beim Bierschaumzerfall kann man nicht vorhersagen, welche Blase als nächstes zerplatzt. Aber bei einer großen Anzahl von Münzen kann man vorhersagen, dass nach dem nächsten Wurf etwa die Hälfte der Münzen "1" zeigt, beim Bierschaumzerfall kann man vorhersagen, dass stets nach einer bestimmten Zeit T nur noch die Hälfte des Bierschaums vorhanden ist. Dies ist beim radioaktiven Zerfall ebenso. Man kann nicht vorhersagen, welcher Atomkern als nächstes zerfällt, aber man kann sagen, dass nach der Halbwertszeit 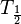 stets etwa die Hälfte der Atomkerne zerfallen ist.
stets etwa die Hälfte der Atomkerne zerfallen ist.

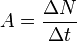 , wobei
, wobei 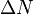 die Anzahl der zerfallenen Kerne ist, die in der Zeit
die Anzahl der zerfallenen Kerne ist, die in der Zeit 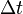 zerfallen sind.
zerfallen sind. .
.

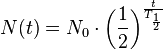
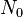 die zur Zeit t = 0s vorhandene Anzahl nicht zerfallener Kerne und
die zur Zeit t = 0s vorhandene Anzahl nicht zerfallener Kerne und