Umkehrfunktion Graph
Mit dem Graph einer Funktion kann man leicht zu einem 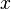 -Wert den
-Wert den  -Wert bestimmen, indem man z.B. bei
-Wert bestimmen, indem man z.B. bei 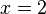 von der x-Achse senkrecht nach oben geht bis man den Graph trifft. In diesem Punkt geht man waagrecht zur y-Achse und bekokmmt den
von der x-Achse senkrecht nach oben geht bis man den Graph trifft. In diesem Punkt geht man waagrecht zur y-Achse und bekokmmt den 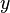 -Wert. Für das Beispiel ist dann
-Wert. Für das Beispiel ist dann 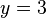 .
.
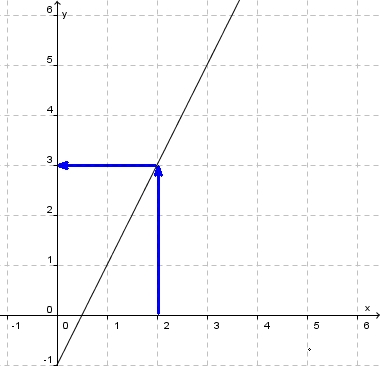
Geht man diesen Weg umgekehrt, also von 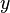 -Wert auf der y-Achse (z.B.
-Wert auf der y-Achse (z.B. 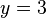 ) waagrecht bis zum Graph und von diesem Punkt senkrecht nach unten zur x-Achse, dann erhält man den
) waagrecht bis zum Graph und von diesem Punkt senkrecht nach unten zur x-Achse, dann erhält man den 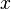 -Wert. Im Beispiel
-Wert. Im Beispiel 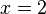 .
.
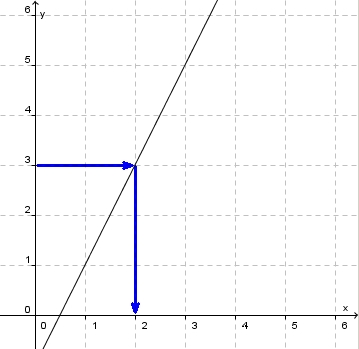
Jetzt ist nur ungewohnt, dass man von der y-Achse losgeht und über den Graph zur x-Achse kommt. Vertauscht man x- und y-Achse, dann hat man wieder das gewohnte Bild.
x- und y-Achse kann man durch eine Achsenspiegelung an der Geraden y = x (Winkelhalbierende des I. und III. Quadranten, 1. Mediane) vertauschen. Natürlich wird dann der Graph der Funktion 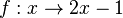 auch gespiegelt und man erhält den Graph der Funktion
auch gespiegelt und man erhält den Graph der Funktion 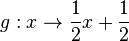 .
.
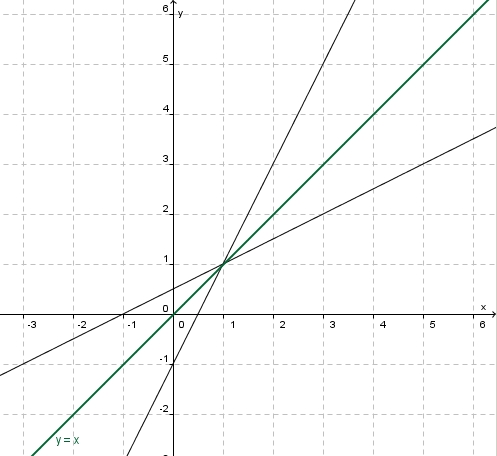
30px Aufgabe
Zeichne in den Graphen die Pfeile, die Welchen |
30px Merke
So erhältst du den Graphen der Umkehrfunktion 1. Zeichne den Graphen der Funktion 2. Zeichne die Gerade 3. Spiegele den Graphen der Funktion |
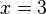 den
den 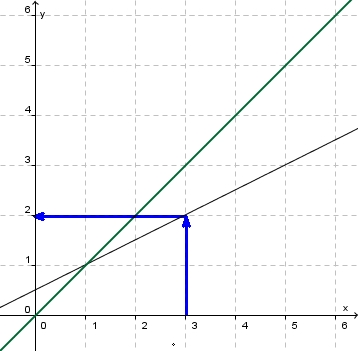
 .
.
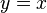 in das Diagramm.
in das Diagramm.

