Gebrochen-rationale Funktionen 8
30px Merke
Eine Funktion f ist eine gebrochen-rationale Funktion, wenn ihr Funktionsterm einen Bruch enthält, in dessen Nenner die Variable x vorkommt. |
Beispiele für Funktionsterme gebrochen-rationaler Funktionen sind 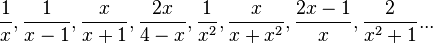 .
.
Im Nenner eines Bruches darf nie 0 stehen. Deshalb muss man diese Wert aus der Grundmenge Q (Menge der rationalen Zahlen) herausnehmen. Alle Zahlen, die man in den Term einsetzen darf stehen auch bei gebrochen-rationalen Funktionen in der Definitionsmenge D.
Um die Definitionslücke zu finden musst du den Nenner gleich 0 setzen und diese Gleichung lösen. Die erhaltenen Zahlen sind aus der Grundmenge Q zu entfernen.
 hat D = Q\{0},
hat D = Q\{0},
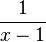 hat D = Q \{1},
hat D = Q \{1},
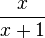 hat D = Q\{-1},
hat D = Q\{-1},
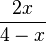 hat D = Q\{4},
hat D = Q\{4},
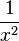 hat D = Q\{0},
hat D = Q\{0},
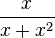 hat D = Q\{-1;0},
hat D = Q\{-1;0},
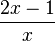 hat D = Q\{0}
hat D = Q\{0}
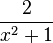 hat D = Q. Beachte, dass es in der Menge Q der rationalen Zahlen keine Zahl gibt, die quadriert -1 ergibt.
hat D = Q. Beachte, dass es in der Menge Q der rationalen Zahlen keine Zahl gibt, die quadriert -1 ergibt.
1. Der Bruchterm ist für
a) x = 0
b) x = 1
c) x = -2
d) x = -1
e) x = 2
f) x = -3 und x = 3
g) x = -5 und x = 5
h) x = 2,5
i) x = 2
j) x = -4 und x = 4
k) x = 0,5
l) x = -1 und x = 0
nicht definiert.
2. a) Im Funktionsterm kommt kein Bruch vor.
b) 4+x2 ist stets größer oder gleich 4, also nie 0.
c) Der Nenner lässt sich umformen; 3(x+1) - 3x = 3, also kann nie 0 werden.
1. Die Definitionslücke ist gegeben. Der Term soll eine gebrochen-rationale Funktion darstellen, d.h. es ist ein Bruchterm mit x im Nenner. Die Definitionslücke ist Nullstelle des Nenners.
a)Die Definitionslücke ist bei x = 0,1. 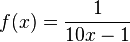
b) Definitionslücken bei x = 0 und x = 1. 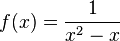
Beachte x2 - x = x(x-1) und ein Produkt ist 0, wenn ein Faktor 0 ist!
c) keine Definitionslücke. 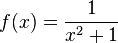
d) Definitionslücken bei x = -1, x = 0 und x = 1. 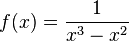
Beachte x3 - x2 = x(x2-1)=x(x-1)(x+1) und ein Produkt ist 0, wenn ein Faktor 0 ist!
2. Man setzt die x-Werte in den Funktionsterm ein. Ergibt sich der angegebene y-Wert, dann liegt der Punkt auf dem Funktionsgraph, ergibt sich ein anderer Wert als angegeben, dann liegt der Punkt nicht auf dem Funktionsgraph. Ist der angegebene Wert größer als der berechnete Wert, dann liegt der Punkt über dem Graphen, ist der angegebene Wert kleiner, dann liegt der Punkt unter dem Graphen.
a) f(3) = 1, also liegt A auf dem Graph, f(0) = 1 < 2,5, also liegt B über dem Graphen, f(4) = 0,5 < 3,5, also liegt C über dem Graphen.
b) f(0) = 12 > 8, also liegt A unter dem Graphen, f(1) = 2,4 < 4, also liegt B über dem Graphen, f(-1) = 6 > -4, also liegt C unter dem Graphen.
Die Funktion der indirekten Proportionalität 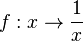 für
für 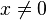 ist die einfachste gebrochen-rationale Funktion.
ist die einfachste gebrochen-rationale Funktion.
Ihr Graph ist eine Hyperbel und besteht aus zwei Hyperbelästen.
An der Stelle x = 0 ist die Funktion nicht definiert. Ihr Graph nähert sich der y-Achse (x = 0) beliebig nahe an. Die y-Achse ist eine senkrechte Asymptote. Betrachtet man die Funktion für sehr große x, d.h. 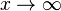 oder sehr kleine x, d.h.
oder sehr kleine x, d.h. 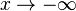 dann nähert sich der Graph beliebig nahe an die x-Achsse an. Die x-Achse ist eine waagrechte Asymptote.
dann nähert sich der Graph beliebig nahe an die x-Achsse an. Die x-Achse ist eine waagrechte Asymptote.
30px Merke
Eine Gerade heißt Asymptote zum Funktionsgraf Gf, wenn sich der Funktionsgraph beliebig nahe an die Gerade annähert ohne sie zu berühren. |
a) Hier sind viele lineare Funktionen dabei. Die musst du richtig herausfinden. Desweiteren ist Graph 2 eine Hyperbel und Graph 4 eine Parabel.
Den Geraden kannst du leicht die richtigen Funktionsgleichungen zuordnen:
Graph 1 und Gleichung II, Graph 3 und Gleichung V, Graph 5 und Gleichung I, Graph 6 und Term VI.
Die Hyperbel (Graph 2) gehört zu einer Bruchgleichung, also Gleichung IV.
Dann bleibt für die Parabel (Graph 4) nur die Gleichung III.
Im Nenner steht der Term x. Dieser nimmt für x=0 den Wert 0 an, also darf man 0 nicht in den Term  einsetzen. x=0 ist Definitionslücke und D = Q\{0}.
einsetzen. x=0 ist Definitionslücke und D = Q\{0}.
Wertetabelle:
![]()
Für x = 0 ist der Term nicht definiert, also taucht 0 auch nicht in der Wertetabelle auf. Falls du 0 in der Wertetabelle hast, dann schreibe beim zugehörigen y-Wert n.d. für nicht definiert.
Graph:
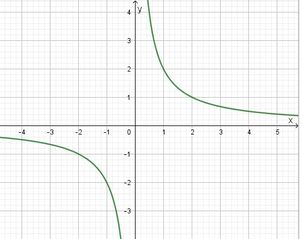
b) y = 0 (x-Achse) ist waagrechte Asymptote, x = 0 (y-Achse) ist senkrechte Asymptote. Der Graph nähert sich den Koordinatenachsen beliebig nahe an ohne sie zu erreichen.
c) In der Wertetabelle siehst du f(4) = 0,5. Wird x größer, dann werden die y-Werte kleiner. Das siehst du auch an der Wertetabelle aber auch am Graphen. Also für x > 4 sind die Funktionswerte f(x) kleiner 0,5.
d) yP = -0,5 und yP* = 0,5. Die Gerade durch P und P* hat die Gleichung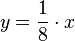 , ist eine Ursprungsgerade und geht also durch den Ursprung.
, ist eine Ursprungsgerade und geht also durch den Ursprung.
Im folgenden Graph ist für b = 0 die Funktion 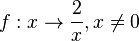 dargestellt. Diese Funktion ist dir aus der letzten Aufgabe bekannt. Ihre senkrechte Asymptote (x=0) ist rot eingezeichnet.
dargestellt. Diese Funktion ist dir aus der letzten Aufgabe bekannt. Ihre senkrechte Asymptote (x=0) ist rot eingezeichnet.
Eigentlich siehst du den Graph der Funktion 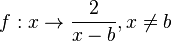 . Für b ist nur der Wert 0 eingestellt. Mit dem Schieberegler (b = 0) kannst du den Wert von b verändern.
. Für b ist nur der Wert 0 eingestellt. Mit dem Schieberegler (b = 0) kannst du den Wert von b verändern.
a) Die Funktion 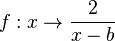 hat bei x = b eine Definitionslücke. D = Q\{b}. b nimmt stets den durch den Schieberegler eingestellten Wert an.
hat bei x = b eine Definitionslücke. D = Q\{b}. b nimmt stets den durch den Schieberegler eingestellten Wert an.
b) Der Graph wird für positive b nach rechts (in positive x-Richtung) verschoben. Für negative b wird er nach links (in negative x-Richtung) verschoben.
c) Es handelt sich auch hier um eine Hyperbel.
d) x = b, wobei b der gerade am Schieberegler eingestellte Wert ist.
e) Die senkrechte Asymptote wird wie der Graph verschoben, also für b > 0 nach rechts und für b < 0 nach links.
f) Die waagrechte Asymptote ist die x-Achse y = 0. Sie ändert sich bei Betätigung des Schiebereglers nicht.
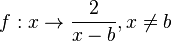 ist nicht definiert für x = b, dort hat sie eine Defintionslücke, ihre Definitionsmenge ist D = Q\{b}. Ihr Graph ist eine Hyperbel. Man erhält diese Hyperbel, indem man die Hyperbel der Funktion
ist nicht definiert für x = b, dort hat sie eine Defintionslücke, ihre Definitionsmenge ist D = Q\{b}. Ihr Graph ist eine Hyperbel. Man erhält diese Hyperbel, indem man die Hyperbel der Funktion 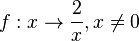 um b in Richtung der x-Achse verschiebt. Die Hyperbel hat zwei Asymptoten, eine senkrechte Asymptote x = a und eine waagrechte Asymptote y = 0 (unabhängig von a).
um b in Richtung der x-Achse verschiebt. Die Hyperbel hat zwei Asymptoten, eine senkrechte Asymptote x = a und eine waagrechte Asymptote y = 0 (unabhängig von a).
Ausgangspunkt im folgenden Applet ist wieder wie gerade eben der Graph der Funktion 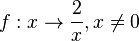 . Desweiteren ist die waagrechte Asymptote y = 0 lila eingezeichnet. Diesmal ist ein Schieberegler für c gegeben. Wir wollen als nächstes Funktionen betrachten, bei denen zum Funktionsterm
. Desweiteren ist die waagrechte Asymptote y = 0 lila eingezeichnet. Diesmal ist ein Schieberegler für c gegeben. Wir wollen als nächstes Funktionen betrachten, bei denen zum Funktionsterm  der Wert von c addiert wird. Wir haben dann also eine Funktion
der Wert von c addiert wird. Wir haben dann also eine Funktion 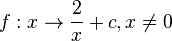 . Eingestellt ist der Wert c = 0. Bewegst du den Schieberegler, ändert sich der Wert von c.
. Eingestellt ist der Wert c = 0. Bewegst du den Schieberegler, ändert sich der Wert von c.
a) a) Die Funktion 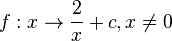 hat bei x = 0 eine Definitionslücke. D = Q\{0}. Sie ändert sich bei Variation von c nicht.
hat bei x = 0 eine Definitionslücke. D = Q\{0}. Sie ändert sich bei Variation von c nicht.
b) Der Graph wird für positive c nach oben (in positive y-Richtung) verschoben. Für negative c wird er nach unten (in negative y-Richtung verschoben.
c) Es handelt sich auch hier um eine Hyperbel.
d) y = c, wobei c der gerade am Schieberegler eingestellte Wert ist.
e) Die waagrechte Asymptote wird wie der Graph verschoben, also für c > 0 nach oben und für c < 0 nach unten.
f) Die senkrechte Asymptote ist die y-Achse x = 0. Sie ändert sich bei Betätigung des Schiebereglers nicht.
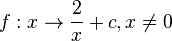 ist nicht definiert für x = 0, dort hat sie eine Defintionslücke, ihre Definitionsmenge ist D = Q\{0}. Ihr Graph ist eine Hyperbel. Man erhält diese Hyperbel, indem man die Hyperbel der Funktion
ist nicht definiert für x = 0, dort hat sie eine Defintionslücke, ihre Definitionsmenge ist D = Q\{0}. Ihr Graph ist eine Hyperbel. Man erhält diese Hyperbel, indem man die Hyperbel der Funktion 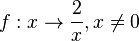 um c in Richtung der y-Achse verschiebt.Die Hyperbel hat zwei Asymptoten, eine senkrechte Asymptote x = 0 (unabhängig von c) und eine waagrechte Asymptote y = c.
um c in Richtung der y-Achse verschiebt.Die Hyperbel hat zwei Asymptoten, eine senkrechte Asymptote x = 0 (unabhängig von c) und eine waagrechte Asymptote y = c.|
Merke:
1. Die Funktion 2. Die Funktion Fasst man beide Aussagen zusammen, dann erhält man: 3, Die Funktion |
Die Veränderung von b und c kannst du im folgenden Applet ausprobieren.
Zuerst ist die Funktion 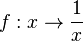 dargestellt. Es gibt zwei Schieberegler. Damit kannst du den Wert der Parameter
dargestellt. Es gibt zwei Schieberegler. Damit kannst du den Wert der Parameter 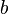 und
und  verändern.
verändern. 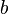 ist ein Parameter, der im Nenner der Funktion als
ist ein Parameter, der im Nenner der Funktion als 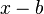 hinzugefügt wird,
hinzugefügt wird,  wird beim Funktionsterm addiert, so dass du die Funktion
wird beim Funktionsterm addiert, so dass du die Funktion 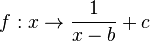 betrachten kannst.
betrachten kannst.
1. Die Gerade x = b ist an der Stelle der Defintionslücke x = b. Bei Veränderung von b, ändert sich die Definitionslücke, die Gerade wandert mit.
Die Gerade x = b ist eine senkrechte Asymptote.
2. Die x-Achse wird um c in y-Richtung verschoben. Die Gerade y = c ist, da sich die Hyperbeläste für große x an sie annähern, Asymptote für  .
.
S. 117/9: a) Eine Punktspiegelung am Ursprung gibt x- und y-Werten jeweils das andere Vorzeichen, also 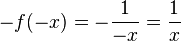 . Dies ist derselbe Funktionsterm wie bei f. Wenn man den Graph von f gezeichnet hat, sieht man, dass er punktsymmetrisch zum Ursprung ist!
. Dies ist derselbe Funktionsterm wie bei f. Wenn man den Graph von f gezeichnet hat, sieht man, dass er punktsymmetrisch zum Ursprung ist!
b) Spiegelt man an der y-Achse, dann bekommen die x-Werte das andere Vorzeichen, also 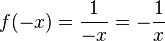 .
.
c)Spiegelt man an der x-Achse, dann bekommen die y-Werte das andere Vorzeichen, also 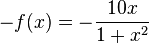 .
.
Übrigens sieht man auf S. 114, dass der Graph punktsymmetrisch zum Ursprung ist.
S. 117/10: A - 2 - III, da: f hat keine Definitionslücke, also III; f(2) = 1, also (2)
B - 4 - I, da f(2) = 0,375 ≈ 0,4, also (4) und f hat bei x = -2 eine Definitionslücke, also I
C - 3 - IV, da f(2) ist nicht definiert, also (3) und f hat bei x = 2 eine Definitionslücke, also IV
D - 1 - II, da f(2) = 3, also (1) und f hat bei x = -2 eine Definitionslücke
S. 117/11:
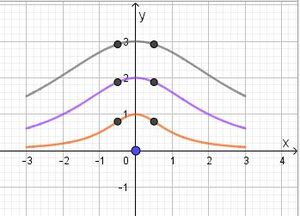
Den Flächeninhalt eines Dreiecks berechnet man mit der Formel 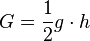 .
Es ist f1(±0,5) = 0,8; f2(±0,5) ≈ 1,88; f3(±0,5) ≈ 2,92.
.
Es ist f1(±0,5) = 0,8; f2(±0,5) ≈ 1,88; f3(±0,5) ≈ 2,92.
Die Funktionswerte geben die Höhe des Dreiecks an, die Grundlinie hat Länge 1 (Abstamd der Punkte auf den Graphen), also ergibt sich
A1 = 0,4; A2 ≈ 0,92; A1 ≈ 1,46.
Nur kurz als Bemerkung: Die Graphen schauen richtig schön aus, wenn man sie für eine größere Definitionsmenge zeichnet.
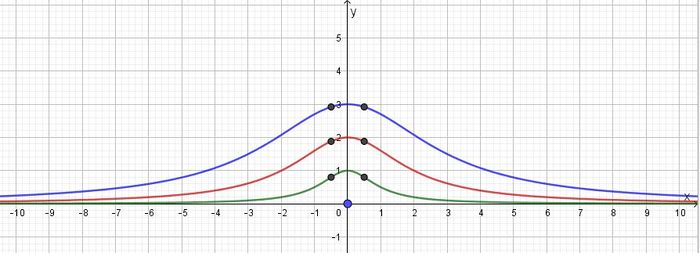
S. 117/12: Man zeichnet den Graph der gegebenen Funktion 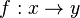 mit
mit 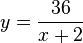 und trägt die gegebenen Punkte mit den Koordinaten aus der Wertetabelle ein. Dann prüft man, ob die Punkte auf dem Graph liegen.
und trägt die gegebenen Punkte mit den Koordinaten aus der Wertetabelle ein. Dann prüft man, ob die Punkte auf dem Graph liegen.
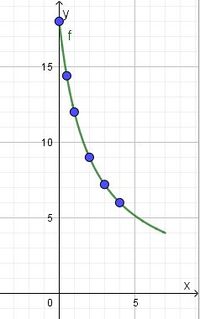
Man kann damit sagen, dass die Temperatur durch den Ansatz 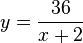 beschrieben werden kann.
beschrieben werden kann.
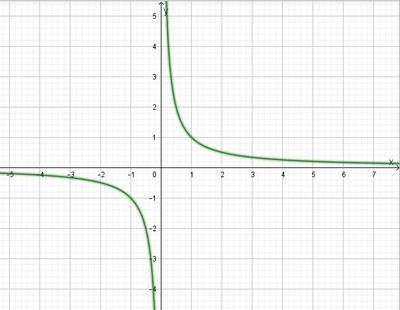
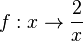 die Definitionsmenge an und zeichne mit Hilfe einer Wertetabelle den Graphen.
die Definitionsmenge an und zeichne mit Hilfe einer Wertetabelle den Graphen.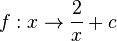 eine Definitionslücke? Gib die Definitionsmenge an.
b) Was passierte mit dem gezeichneten Graphen für c = 0 als du den Schieberegler bewegt hast?
eine Definitionslücke? Gib die Definitionsmenge an.
b) Was passierte mit dem gezeichneten Graphen für c = 0 als du den Schieberegler bewegt hast?
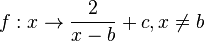 ist nicht definiert für x = b, dort hat sie eine Defintionslücke, ihre Definitionsmenge ist D = Q\{b}. Ihr Graph ist eine Hyperbel. Man erhält diese Hyperbel, indem man die Hyperbel der Funktion
ist nicht definiert für x = b, dort hat sie eine Defintionslücke, ihre Definitionsmenge ist D = Q\{b}. Ihr Graph ist eine Hyperbel. Man erhält diese Hyperbel, indem man die Hyperbel der Funktion 
