M11 Rechnen mit Vektoren

Man kann mit Vektoren auch rechnen. Es gibt zwei Rechenarten für Vektoren, die Addition und die S-Mulitplikation.

Merke Addition von Vektoren Vektoren kann man addieren. Dazu setzt man an die Spitze des einen Vektors (natürlich an einen Repräsentanten von ihm!) den Anfangspunkt des anderen Vektors. Der Pfeil vom Anfangspunkt des ersten Vektors zum Endpunkt des zweiten Vektors ist der Summenvektor.

Rechnerisch heißt das, dass man die Koordinaten der Vektoren addiert, man spricht von koordinatenweiser Addition.
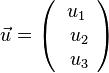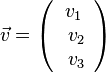Für die Vektoren $\vec u = \left ( \begin{array}{c} u_1 \\\ u_2 \\\ u_3 \end{array}\right)$ und $\vec v = \left ( \begin{array}{c} v_1 \\\ v_2 \\\ v_3 \end{array}\right)$ gilt dann für den Summenvektor $\vec w = \vec u + \vec v = \left ( \begin{array}{c} u_1 \\\ u_2 \\\ u_3 \end{array}\right) + \left ( \begin{array}{c} v_1 \\\ v_2 \\\ v_3 \end{array}\right)= \left ( \begin{array}{c} u_1+v_1 \\\ u_2+v_2 \\\ u_3+v_3 \end{array}\right)$ .
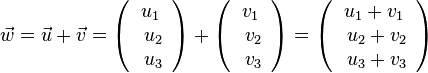Die Koordinaten des Summenvektors sind die Summen der Koordinaten der Summanden.