M11 Anwendungen und Aufgaben zum Rechnen mit Vektoren
In den folgenden Bildern sind die Vektoren ohne Vektorpfeil angegeben. Leider macht GeoGebra das nicht.
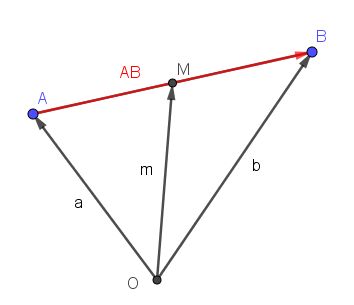
Die Strecke [AB] hat einen Mittelpunkt M, dessen Ortsvektor ist 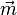 .
.
|
Merke:
Der Ortsvektor 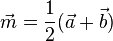 |
Wie kommt man vom Ursprung zu M?
Man geht zuerst mit dem Vektor  zum Punkt A und dann die Hälfte der Strecke [AB], dies geht mit dem Vekor
zum Punkt A und dann die Hälfte der Strecke [AB], dies geht mit dem Vekor 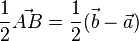 . Also insgesamt
. Also insgesamt 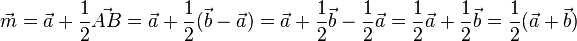 .
.
![\vec m = \frac{1}{2} \left [ \left ( \begin{array}{c} 1 \\\ 2 \\\ 3 \end{array}\right) + \left ( \begin{array}{c} 6 \\\ 5 \\\ 4 \end{array}\right) \right ] = \frac{1}{2} \left ( \begin{array}{c} 7 \\\ 7 \\\ 7 \end{array}\right) = \left ( \begin{array}{c} 3,5 \\\ 3,5 \\\ 3,5 \end{array}\right)](/images/math/a/3/c/a3c7b12f5314a6b152960748520bf2a5.png) , also M(3,5;3,5;3,5)
, also M(3,5;3,5;3,5)
![\vec m = \frac{1}{2} \left [ \left ( \begin{array}{c} -1 \\\ 2 \\\ 3 \end{array}\right) + \left ( \begin{array}{c} 6 \\\ 0 \\\ -4 \end{array}\right) \right ] = \frac{1}{2} \left ( \begin{array}{c} 5 \\\ 2 \\\ -1 \end{array}\right) = \left ( \begin{array}{c} 2,5 \\\ 1 \\\ -0,5 \end{array}\right)](/images/math/f/3/0/f306226783f22a7c9c91ce329df9c42e.png) , also M(2,5;1;-0,5)
, also M(2,5;1;-0,5)
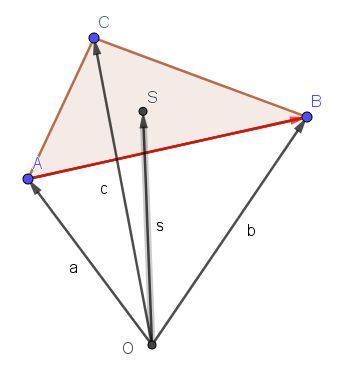
Ein ähnliches Ergebnis erhält man für den Schwerpunkt S eines Dreiecks mit den Eckpunkten A, B, C.
|
Merke:
Der Schwerpunkt S eines Dreiecks mit den Eckpunkten A, B, C und deren Ortsvektoren 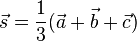 . . |
Wie kommt man vom Urpsung zu S?
Sind Ma, Mb und Mc die Mittelpunkte der Dreiecksseiten a, b, c.
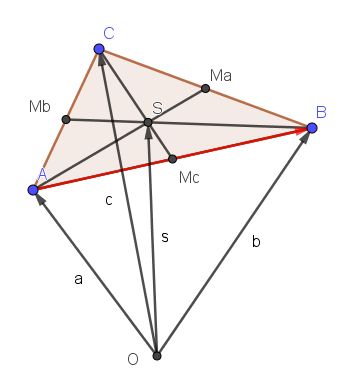
Man geht zurest mit dem Vektor  zum Punkt A, dann von A nach Mb und von Mb nach S, also
zum Punkt A, dann von A nach Mb und von Mb nach S, also
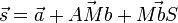
Nun ist 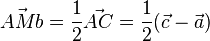 und
und ![\vec {MbS}=\frac{1}{3} \vec {MbB} = \frac{1}{3}(\vec b - \vec {Mb})=\frac{1}{3}[\vec b - \frac{1}{2}(\vec c + \vec a)]](/images/math/d/7/a/d7a561887d1ea3a28dc61125d5e3bea7.png)
Damit ist ![\vec s = \vec a+ \vec {AMb} + \vec {MbS} = \vec a + \frac{1}{2}(\vec c -\vec a) + \frac{1}{3}[\vec b - \frac{1}{2}(\vec c + \vec a)]=\vec a + \frac{1}{2} \vec c - \frac{1}{2} \vec a + \frac{1}{3} \vec b - \frac{1}{6} \vec c - \frac{1}{6}\vec a = \frac{1}{3} \vec c + \frac{1}{3} \vec b + \frac{1}{3} \vec b = \frac{1}{3} (\vec a + \vec b + \vec c)](/images/math/8/b/6/8b61a33bf8f1d7262d008bbe91303e66.png)
Hinweis: 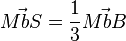 erhält man aus dem Strahlensatz!
erhält man aus dem Strahlensatz!
![\vec s = \frac{1}{3} \left [ \left ( \begin{array}{c} 1 \\\ 2 \\\ 3 \end{array}\right) + \left ( \begin{array}{c} 6 \\\ 5 \\\ 4 \end{array}\right) + \left ( \begin{array}{c} 5 \\\ 2 \\\ -1 \end{array}\right) \right ] = \frac{1}{3} \left ( \begin{array}{c} 12 \\\ 9 \\\ 6 \end{array}\right) =\left ( \begin{array}{c} 4 \\\ 3 \\\ 2 \end{array}\right)](/images/math/8/d/4/8d44ac09238feb21c794a23f61b312ff.png) , also S(4;3;2).
, also S(4;3;2).
Die Seitenlängen des Dreiecks sind: 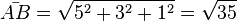 ,
, 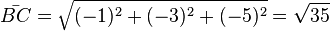 ,
, 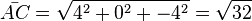 , also ist das Dreieck gleichschenklig.
, also ist das Dreieck gleichschenklig.
Es ist 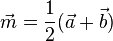
a) 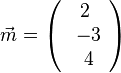
b) 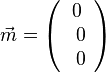
c) 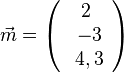
d) 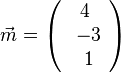
e) 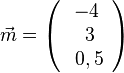
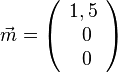
Die beiden Formeln zum Mittelpunkt einer Strecke und Schwerpunkt eines Dreiecks stehen in der Merkhilfe!
98/8
Im Bild im Buch sind die Vektoren 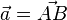 und
und 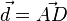 gegeben. Desweiteren weiß man
gegeben. Desweiteren weiß man 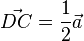 . Dann sind:
. Dann sind:
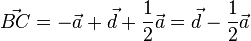 ,
,
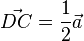
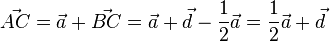
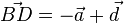
98/9 Es ist C(0;4;0) und D(0;0;0). C und D ergeben sich eindeutig, da die Pyramide gerade ist. Eine Pyramide ist gerade, wenn ihr Höhenfußpunkt gleich dem Mittelpunkt des Umkreises der Grundfläche ist.
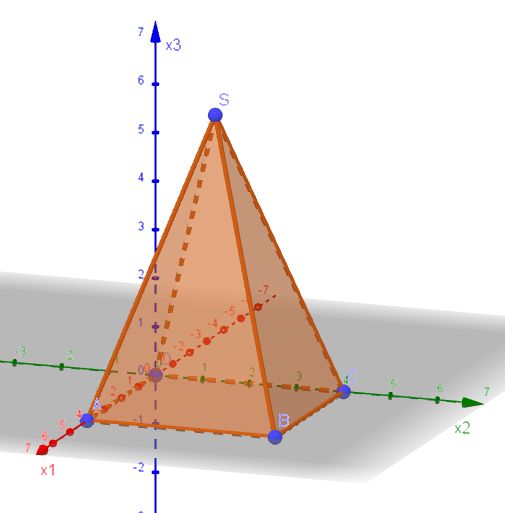
a) 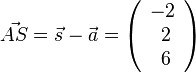
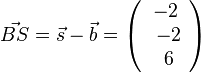
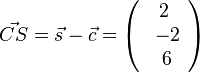
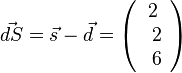
b) Es ist O = 4·A + G, wenn A eine Seitenfläche und G die Grundfläche ist.
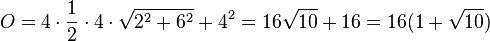
Der Winkel SBC im Dreieck SBC ist der gleiche wie im Dreieck SBF, wenn F der Höhenfusspunkt der Höhe von S auf [BC] ist. Das hat den Vorteil, dass das Dreieck SBF bei F rechtwinklig ist. Dann ist 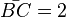 und
und 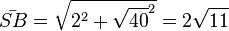 . Dann ist im Dreieck SBF der Winkel
. Dann ist im Dreieck SBF der Winkel  durch
durch 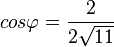 gegeben und es ist
gegeben und es ist 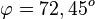 .
.
99/14
Den Bildpunkt P* erhält man durch 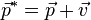 .
.
a) 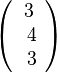
b) 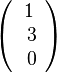
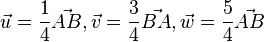 .
.|
Der Teilpunkt T teilt eine Strecke [AB] im Teilverhältnis Dabei ist zu beachten, dass hier die Reihenfolge eine Rolle spielt. Wenn T die Strecke [AB] teilt, dann geht man von A zu T und dann von T zu B. Dann ist Durch die Verwendung von Vektoren hat man den Vorteil, dass das Teilverhältnis auch negativ sein kann. Man definiert: 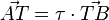 Da Vektoren auch entgegengesetzt gerichtet sein können ist nun auch ein negatives
Mehr dazu auf Wikipedia. |
a) T ist der Mittelpunkt von [AB].
b) 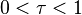
c) 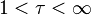
d) 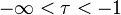
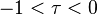

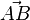 der zwei Punkte mit den Ortsvektoren
der zwei Punkte mit den Ortsvektoren 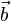 ist
ist 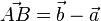 .
.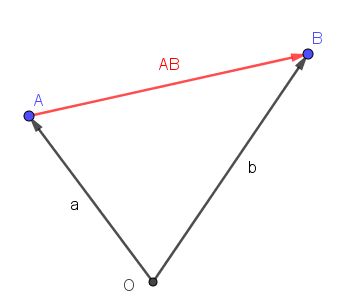
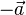 gehen und dann in Richtung
gehen und dann in Richtung 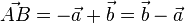 .
.
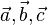 hat den Ortsvektor
hat den Ortsvektor 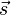 . Es ist
. Es ist 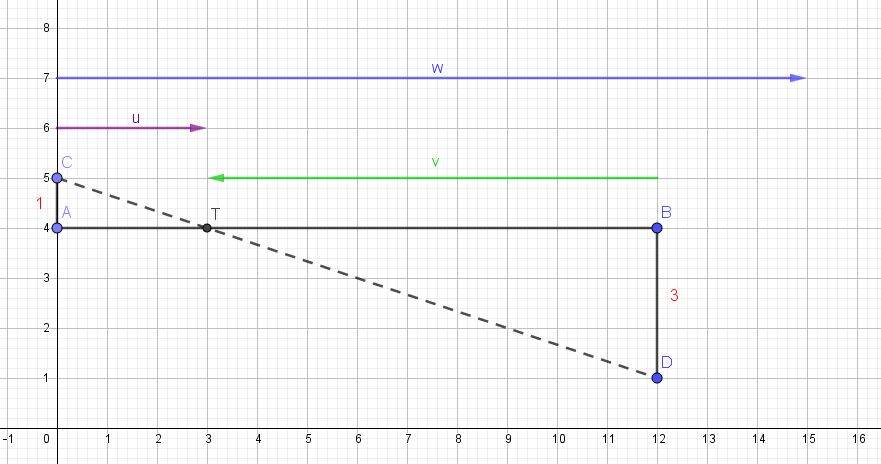
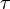 . Dabei ist
. Dabei ist 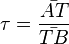 .
.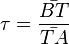 .
.
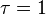 ?
?
