Diskussion:M11 Skalarprodukt

Buch S. 112 / 10
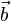Die Vektoren $\vec a$ und $\vec b$ stehen senkrecht aufeinander, d.h. 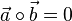$\vec a 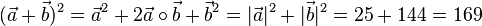\circ \vec b 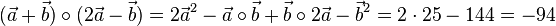= 0$.
a) $(\vec a + \vec b)^2 =\vec a^2 + 2\vec a \circ \vec b + \vec b^2=|\vec a|^2 + |\vec b|^2=25+144=169$
b) $(\vec a + \vec b) \circ (2\vec a - \vec b)=2\vec a^2-\vec a \circ \vec b+\vec b \circ 2\vec a - \vec b^2= 2 \cdot 25 - 144 =-94$
c) Eine Hommage an die binomischen Formeln!
$(\vec a + \vec b)^2+(\vec a - \vec b)^2+(\vec a + \vec b)(\vec a -a\vec b) = \vec a^2 + 2 \vec a \circ \vec b + \vec b^2 + \vec a^2 - 2 \vec a \circ \vec b + \vec b^2 + \vec a^2 - \vec b^2= 25 + 144 +25 +144 + 25 -144 = 219$

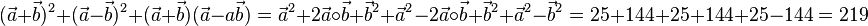
Buch S. 112 / 14
Man weiß aus der Mittelstufe, dass der Flächeninhalt eines Parallelogramms A = gh ist. D.h. fälllt man von der Spitze von 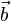$\vec b$ das Lot auf $\vec a$ erhält man die Höhe h.
a steht für 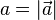$a=|\vec a|$ und b für 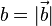$b=|\vec b|$. Es ist dann 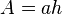$A = ah$ und h ist 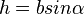$h=b sin\alpha$, also 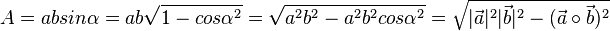$A=absin\alpha =ab\sqrt {1-cos\alpha^2} =\sqrt {a^2b^2-a^2b^2cos\alpha^2}=\sqrt{|\vec a|^2|\vec b|^2- (\vec a \circ \vec b)^2}$ q.e.d.
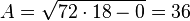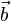b) $A=\sqrt{72\cdot 18 -0}=36$ (Beachten Sie, dass $\vec a$ und $\vec b$ senkrecht zueinander sind.

c)

Buch S. 113 / 16
a) A(2;0,0), B(0;2;0), C(0;0;2) und S(0;0;0)