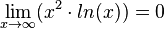M11 Besondere Grenzwerte mit ln- und e-Funktion

In der Merkhilfe sind drei Grenzwerte aufgeführt.

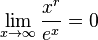
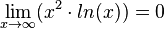Merke: Für r > 0 ist $\lim_{x \to \infty}\frac{x^r}{e^x} = 0$ $\lim_{x \to \infty}\frac{ln(x)}{x^r} = 0$ $\lim_{x \to \infty}(x^2\cdot ln(x) ) = 0$

Zur Veranschaulichung sind diese drei Applets, mit denen die Grenzwertaussagen plausibel gemacht werden:
In den Applets kann man zoomen, die Achsenverhältnisse ändern und das Graphikblatt verschieben.

1. $\lim_{x \to \infty}\frac{x^r}{e^x} = 0$

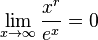
2. $\lim_{x \to \infty}\frac{ln(x)}{x^r} = 0$

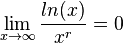
3. $\lim_{x \to \infty}(x^2\cdot ln(x) ) = 0$