|
Merke:
Wird ein Zufallsexperiment in mehreren Schritten ausgeführt, so nennt man es mehrstufig oder zusammengesetzt.
Mehrstufige Zufallsexperimente lassen sich schön durch Baumdiagramm veranschaulichen.
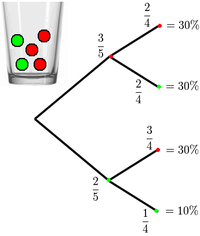
Bei den Teilpfaden notiert man die jeweilige Wahrscheinlichkeit.
Beim Baumdiagramm gelten die drei Pfadregeln:
1. Pfadregel
Der Summenwert der Wahrscheinlichkeiten auf den Teilpfaden, die von einem Verzweigungspunkt ausgehen, ist 1.
Im Beispiel nach dem linken Verzweigungspunkt ist 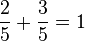 . Rechts ist nach dem zweiten unteren Verzweigungspunkt . Rechts ist nach dem zweiten unteren Verzweigungspunkt 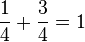 und nach dem zweiten oberen Verzweigungspunkt und nach dem zweiten oberen Verzweigungspunkt 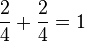 . .
2. Pfadregel
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten auf dem Pfad, der zu dem Ergebnis führt.
Im Beispiel ist 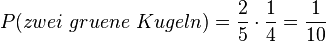 , ,
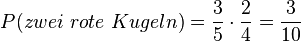 , ,
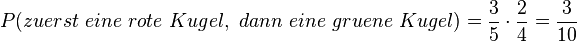 , ,
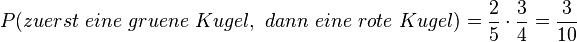
3. Pfadregel
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten für die günstigen Ergebnisse für dieses
Ereignis.
Im Beispiel ist 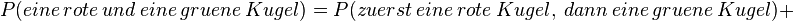
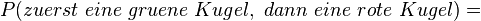 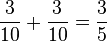
|